Характеристические функции. 
Основные элементы термодинамики

Функция называется характеристической, если её частная производная по некоторому параметру даёт другой параметр, а именно, соответствующий тому, по которому производится дифференцирование.

1. Рассмотрим сопряжение по координатам.

В этом случае в качестве независимо изменяющихся параметров выступают только координаты, а потенциалы отслеживают их изменение по каким-либо зависимостям с участием этих координат.

Как известно, dU — полный дифференциал и U=U (X1, X2,…, Xn). По правилам математики для полного дифференциала функции нескольких переменных:

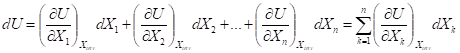
Здесь, Xinv — означает, что все остальные координаты инвариантны, т. е. временно не являются переменными («заморожены»).

Так как:

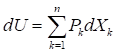
то.

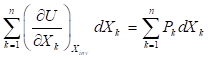
Последнее равенство должно выполняться при любых k, поэтому:

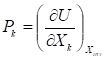
(32).

В соответствии с определением характеристической функции, U является характеристической функцией при сопряжении по координатам. — общее обозначение характеристической функции. Таким образом можно записать:

(Xk) = U (33).

Пример: Термодеформационная система.

Табл. 3.

Из (33) для данного случая:

(S, v)=U (34).

Из (32) получим:

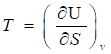
(35).

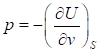
(36).

Так как:

то для термодеформационной системы:

dU=T dS — p dv (38).

Так как TdS = dQ и PdV = dA, то уравнение (38) — это первое начало термодинамики dU = dQ — dA.

2. Рассмотрим сопряжение по потенциалам.

Без вывода, окончательно можно записать:

(39).

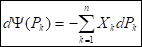
(40).

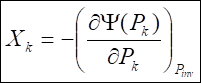
(41).

Рассмотрим в качестве примера термодеформационную систему:

Табл. 4.

Из (39):

(T, p) = U — TS + pv — эта характеристическая функция в термодинамике имеет свое обозначение и название:

= U — TS + pv (42).

где Ф — свободная энтальпия (удельная свободная энтальпия);

По физическому смыслу pv — удельная потенциальная энергия 1 кг сжатой до давления р системы.

Из (40) d = -S dT + v dp (43).

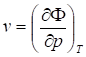
Из (41) =>; .

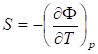
В химической термодинамике свободную энтальпию называют изобарно-изотермическим потенциалом.

3. Рассмотрим смешанное сопряжение:

При таком виде сопряжения в качестве независимых переменных выступают не все n потенциалов, а только r потенциалов. Такие независимые потенциалы обозначим как Pi,.

где i=1,2,3,…, r. (r < n).

Независимые координаты обозначим как Xj,.

где j=(r+1),(r+2),…, n.

Без вывода сразу запишем окончательные соотношения:

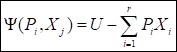
(46),.

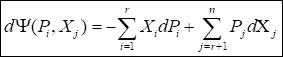
(47).

(48).

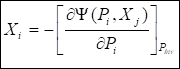
Пример: Рассмотрим термодеформационную систему Табл. 5.

Пусть независимым потенциалом будет — Т, а независимой координатой — v. Из (46) (T, v) = U — TS. Эта характеристическая функция в термодинамике имеет свое обозначение и название F = U — TS (50) — свободная энергия.

В соответствии с (47) запишем дифференциал этой функции:

dF = - S dТ — p dv (51).

Из (48) и (49) получим:

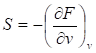
(52),.

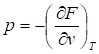
(53).

Из (51) для изотермического процесса (T=const) получим:

dFT = - p dv (54).

Так как p dv = dAдеф, то в изотермических процессах деформационная работа совершается системой за счёт убыли свободной энергии.

В химической термодинамике F называется изохорно-изотермическим потенциалом.

• б) Пусть независимым потенциалом будет (-p), а независимой координатой — S. В соответствии с (46) получим:
  • (p, S) = U + pv (55)

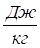
В термодинамике эта характеристическая функция имеет свое название и обозначение i = U + pv — удельная энтальпия, .

Ранее указывалось, что произведение pv — это потенциальная энергия 1 кг газа при давлении p с удельным объёмом v. Покажем это на следующем примере (рис. 7):

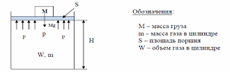
Рис. 7. Схема для определения физического смысла произведения PV.

В равновесии Mg = pS. Умножим обе части этого уравнения на высоту Н, помня, что объем системы W=SH:

Eпот = МgH = pSH = pW.

Удельная потенциальная энергия — это Eпот /m, тогда:

Eпот /m = pW/m = pV.

Из соотношения (47) для термодеформационной системы получим:

di = T dS + v dp (56).

Как известно, T dS = dQ и dAпол= -VdP, тогда:

di = dQ — dAпол или dQ = di + dAпол После интегрирования получим I-е начало термодинамики в так называемой энтальпийной форме:

Q = ?i + Aпол Теплота, подведенная к системе, идет на увеличении ее энтальпии и на совершение системой полезной работы.

Из (56) для изобарного процесса:

dQp = dip (57).

После интегрирования получим:

Qp = i2 — i1 (58).

Таким образом, в изобарных процессах количество теплоты, которой обмениваются система и окружающая среда, равно разности значений энтальпий в конечном и начальном состояниях системы.

Из (56) для адиабатного процесса следует:

dis = -dAпол или Апол = -?is = i1 — i2.

Таким образом, полезная работа в адиабатных процессах равна разности энтальпий в начальном и конечном состояниях системы.

Из (48), (49) получим:

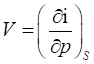
(59).

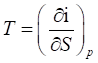
(60).

Так как d — это полный дифференциал, то все характеристические функции (F, U, Ф, i) являются функциями состояния:

ДU = U2 — U1.

ДФ = Ф2 — Ф1.

ДF = F2 — F1.

Дi = i2 — i1.

Как будет показано далее, к функциям состояния относится также энтропия S.

Мнемонический приём для термодеформационной системы:

1) Записываем «четверку» параметров для термодеформационной системы, причем первыми идут параметры теплового взаимодействия (S и Т).

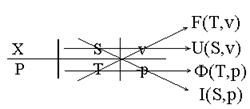
Рис. 8.

• 2) пропускаем «шампуры» через параметры «соседнего» взаимодействия
• 3) пишем «по-японски» вертикально «FUФi»
• 4) дописываем к каждой из «FUФi» параметры «на шампурах»
• 5)в правой части дифференциалов характеристических функций сначала пишем дифференциалы параметров «на шампурах»
• 6) дописываем сомножители к этим дифференциалам, стоящим в правой части по правилу: «каждой твари по паре»
• 7) расставляем знаки по правилу: «послушай женщину и сделай наоборот». Если в произведении первой стоит координата, то знак меняется на противоположный естественному.

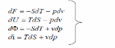
(61).

По своей сути, формулы (61) — это первое начало термодинамики для термодеформационной системы в различных формах записи.

8) выражаем параметры в правой части уравнений (61) не стоящие под знаком дифференциала по правилу: «если очень хочется, то можно»:

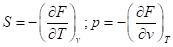
и так далее.