Граничные условия. 
Электростатическое поле

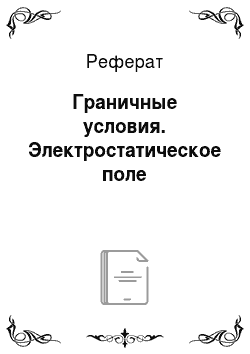
До сих пор рассматривалось электростатическое поле в однородном пространстве. Если имеются две (или более) разнородные среды, то для определения поля необходимо знать граничные условия для составляющих векторов Е и D и потенциала на границе раздела. Электростатическое поле является частным случаем электромагнитного поля. Поэтому граничные условия для векторов Е и D должны выполняться и для электростатического поля. Эти условия имеют вид:

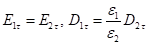
(14).

(15).

Так как при решении конкретных задач, как правило, оперируют с функцией , то от условий для векторов Е и D нужно перейти к граничным условиям для потенциала. Используя соотношение (3) следующее равенство:

(16).

где оператор означает дифференцирование по любому направлению в плоскости, касательной к поверхности раздела в рассматриваемой точке. Интегрируя равенство (16) по , получаем.

(17).

где — произвольная постоянная, а и — значения потенциала и на поверхности раздела в первой и второй средах соответственно.

Рис. 10.

Постоянную в большинстве случаев можно считать равной нулю. Действительно, потенциал и, созданный объемными или поверхностными зарядами, является непрерывной функцией. При этом из равенства (17) следует, что.

(18).

Соотношение (18) нарушается, если на поверхности раздела имеется двойной заряженный слой.

Переходя в формулах (3.14).

к функции и, получаем второе граничное условие для электростатического потенциала:

(19).

где оператор означает дифференцирование по нормали к поверхности раздела, направленной из второй среды в первую.

Если одна из сред является проводником, то граничные условия принимают более простой вид. В самом деле, при анализе макроскопических свойств поля проводник можно рассматривать как замкнутую область, внутри которой возможно свободное перемещение зарядов. Плотность потока зарядов, т. е. плотность тока проводимости в проводнике, пропорциональна напряженности электрического поля:. В электростатике перемещение зарядов отсутствует:. Так как, то напряженность электростатического поля внутри проводника должна быть равна нулю. Это — одна из особенностей электростатического поля. Известно, что переменное электромагнитное поле не проникает в идеальный металл. Электростатическое поле равно нулю внутри любого реального проводника.

Внутри проводника grad и = 0. Откуда и = const. Следовательно, в электростатике все точки проводника имеют один и тот же потенциал. Это позволяет говорить о потенциале проводника. Потенциалы изолированных друг от друга проводников могут, конечно, иметь разные значения.

Найдем граничные условия на поверхности проводника для составляющих векторов Е и D. Пусть первая среда — диэлектрик, а вторая — проводник. Тогда, полагая и, получаем.

(20).

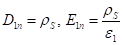
(21).

Условия (3.19) и (3.20) можно переписать в векторной форме:

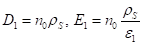
(22).

Подчеркнем, что в случае переменного поля аналогичные условия выполняются лишь на поверхности идеального проводника, а в электростатике условия (20)—(22) справедливы при любой отличной от нуля удельной проводимости второй среды.

Граничные условия для потенциала на поверхности проводника получаются из формул (20) и (21):

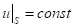
(23).

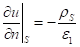
(24).

Нормаль считается внешней по отношению к проводящей среде.

Из условия (23) следует, что поверхность проводника всегда эквипотенциальна.