Перенапряжения при повторных зажиганиях дуги

Если дуга гаснет при первом прохождении высокочастотного тока через нуль (момент t2), то на емкостях здоровых фаз остаются заряды СUBмакс и СUCмакс (для рис. 1.2 UВмакс=UВмакс), а на емкости С фазы, А заряд равен нулю.

После гашения дуги суммарный заряд распределится поровну между емкостями 3-х фаз, которые приобретут одинаковое дополнительное напряжение по отношению к земле U (смещение нейтрали), накладывающееся на напряжение источника.

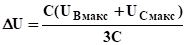
Для рассматриваемого случая, поскольку UВмакс=UCмакс,.

.

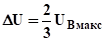
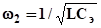
Так как заряды с емкостей здоровых фаз переходят на емкость поврежденной фазы через индуктивность трансформатора, то этот процесс носит колебательный характер с частотой, где Сэ=С + Смф. 2 21.

Амплитуда колебаний равна разности между мгновенным значением вынужденного напряжения на поврежденной фазе непосредственно после обрыва дуги UA (t2) + U и начального напряжения до обрыва дуги равного нулю.

В рассматриваемом примере.

.

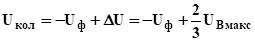
На фазе, А происходит характерный всплеск напряжения, называемый пиком гашения, который приближенно равен.

Uпг 2Uкол= 2[UA (t2) + U].

В нашем случае Uпг= 2(U — Uф).

После затухания колебаний происходит медленный подъем напряжения с частотой источника. Одновременно с изменением восстанавливающегося напряжения по кривой UA (рис. 1.2) происходит восстановление электрической прочности дугового промежутка по кривым А, Б или В.

Случай, А характерен для небольших сетей с малой емкостью С, у которых дуга ликвидируется в течение одного полупериода промышленной частоты.

Это сети 35 кВ при токах замыкания на землю Iз= 5 10 А и сети 6−10 кВ при Iз= 20 30 А.

В случае Б кривая восстановления электрической прочности дугового промежутка проходит выше Uпг и пересекается с кривой UA вблизи ее максимума. В этот момент дуга вновь загорится, но может опять погаснуть при прохождении через нуль высокочастотного тока. Дуга будет иметь перемежающийся характер.

В случае В повторное зажигание дуги произойдет в момент t3 вскоре после гашения. Зажигание будеь сопровождаться колебательным процессом, но с меньшей амплитудой, т.к. напряжение на здоровых фазах в этот момент приблизилось к установившемуся значению. Вероятность гашения дуги при втором прохождении тока через нуль будет выше, а смещение нейтрали U меньше. Очередная попытка гашения дуги произойдет при следующем прохождении высокочастотного тока через нуль. Если дуга не погаснет во время высокочастотных колебаний, то она может быть погашена при прохождении через нуль тока промышленной частоты. Таким образом в случае В дуга может быть как перемежающейся, так и устойчивой.

Наибольшую опасность для изоляции представляют перемежающиеся дуги, причем наибольшие перенапряжения возникают, когда повторное зажигание происходит приблизительно через полпериода после гашения дуги. Увеличение напряжения в переходном режиме по сравнению с первым зажиганием обусловлено смещением нейтрали U. Как видно из рис. 1.2, в момент t4 увеличивается разность между установившимся значением UAB и напряжением на здоровой фазе UB + U, что и приводит к увеличению амплитуды свободных колебаний.

Для определения максимального напряжения при n-ом зажигании дуги можно воспользоваться формулой определения UB макс, учитывая, что напряжение фазы, А в момент, предшествующий зажиганию, возрастает на величину смещения нейтрали, образовавшегося в результате предыдущего гашения дуги.

Используя эту формулу, рассмотрим некоторые варианты поведения дуги и определим предельные значения перенапряжений.

1. Дуга гаснет при первом прохождении через нуль тока высокочастотных колебаний и зажигается через полпериода в момент максимального напряжения на поврежденной фазе (кривые Б и UA на рис. 1.2) — теория Петерсена.

Этот режим идеализирован и маловероятен, однако он позволяет получить предельные значения перенапряжений.

В табл.1.1 приведены расчетные значения напряжений, полученные по данной теории при k=0,2 и d=0,1.

Как видно из таблицы максимальные перенапряжения и смещение нейтрали растут от полупериода к полупериоду, но темп роста постепенно замедляется, т.к. наряду с процессом накопления зарядов на емкостях, когда дуга не горит, идет процесс стекания зарядов на землю при горении дуги. Постепенно рост перенапряжений прекращается. Предельное значение перенапряжений может быть найдено, приравняв Un макс=U (n-1)макс, и тогда.

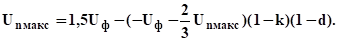
Отсюда.

В рассматриваемом примере Un макс=4,26Uф.

По теории Петерсена напряжение на здоровых фазах может повышаться до 7,5Uф.

Таблица 1.1 Расчетные значения напряжений в относительных единицах

2. Эксперименты в сетях и на моделях, проведенные Н. Н. Беляковым, показали, что дуга может гаснуть при прохождении через нуль как высокочастотного тока, так и тока промышленной частоты. Причем попытка гашения дуги заканчивается удачно, если пик гашения не превышает определенного значения. Например, для сетей 6−10 кВ дуга гаснет, если Uпг 0,4Uф. В свою очередь это условие влияет на смещение нейтрали, которое должно быть не более U=0,5Uпг + Uф=1,2Uф. Если U>1,2Uф, то Uпг>0,4Uф — дуга погаснет и тут же загорится вновь. Заряды емкостей будут частично отводиться на землю. При следующем прохождении высокочастотного тока через ноль будет еще одна попытка гашения дуги и так до тех пор пока значение Uпг не станет меньше 0,4Uф.

После этого дуга гаснет и может загореться лишь под влиянием восстанавливающегося напряжения промышленной частоты приблизительно через полпериода. Используя формулу для Unмакс, можно найти максимальное значение перенапряжений, если подставить в нее следующие значения: U= 1,2Uф; UA= UФsin; UB= Uфsin (120). Тогда при = 90.

Следует отметить, что наибольшие перенапряжения возникают не в момент максимума напряжения на поврежденной фазе, а несколько раньше, что более вероятно.

Теория Белякова дает меньшие значения перенапряжений, чем теория Петерсена, кроме того по ней напряжения нарастают не постепенно, а при втором зажигании дуги (через полпериода). Однако она носит частный характер, т.к. основана на экспериментах, ограниченных определенными условиями. По теории Белякова напряжения на здоровых фазах могут повышаться до 4Uф.

3. По теории Петерса-Слепяна дуга гаснет при переходе через ноль тока промышленной частоты и зажигается вновь при максимальном напряжении промышленной частоты на поврежденной фазе.

В этом случае гашение дуги происходит через полпериода после зажигания, когда свободные колебания затухнут. При этом напряжения на здоровых фазах будут равны 1,5Uф, а U=Uф .

Подставив эти значения в формулу определения максимального напряжения, получим UВ макс =1,5Uф + 2Uф (1 k)(1 d) = 1,94Uф.

По теории Петерса-Слепяна максимальные перенапряжения могут достигать 3,5Uф.

В реальных сетях перенапряжения (3 3,2)Uф являются предельными. Подобные перенапряжения не являются опасными для изоляции класса 35 кВ. Однако длительное их существование может вызвать повреждение ослабленной или загрязненной изоляции. Кроме того, дуга может переброситься на другие фазы. Поэтому дуговое замыкание фазы на землю должно быть ликвидировано возможно быстрее.