Оптимизация формы ступенчато-призматической балки при изгибе

Аннотация: Получено решение задачи оптимизации ступенчато-призматической балки из условия минимума потенциальной энергии деформации при заданном объеме. Задача решена для случая шарнирного опирания по концам и равномерно распределенной по длине нагрузки. Найдено оптимальное значение параметра б, равного отношению высоты средней ступени к высоте крайней, при котором жесткость балки при постоянных объеме и ширине поперечного сечения максимальна.

Ключевые слова: оптимизация, ступенчато-призматическая балка, потенциальная энергия деформации, переменная жесткость, минимальный объем.

ступенчатый балка деформация нагрузка Рассмотрим ступенчато-призматическую балку прямоугольного сечения, шарнирно опертую по концам, загруженную равномерно распределенной нагрузкой q (рис. 1). Пусть ширина балки постоянна и равна b, высота крайних ступеней равна h, а средней ступени — бh.

Рис. 1. — Расчетная схема

Согласно [1,2] интегральной мерой, определяющей уровень напряженно-деформированного состояния, может служить потенциальная энергия деформации U. Чем меньше величина U, тем лучше система сопротивляется внешним воздействиям. При изгибе потенциальная энергия деформации (ПЭД) определяется следующим образом:

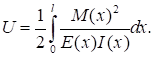
(1).

Найдем такую величину параметра б, при которой потенциальная энергия деформации принимает минимальное значение при заданном объеме балки V. Объем рассматриваемой балки определяется следующим образом:

(2).

Выразим из (2) величину h:

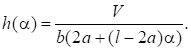
(3).

Для определения оптимального значения б потребуется вычислить производную :

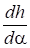
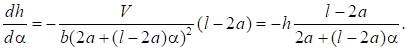
(4).

Моменты инерции крайних ступеней и средней ступени определяются следующим образом:

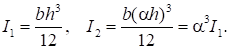
(5).

Выражение для изгибающего момента имеет вид:

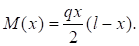
(6).

Подставив (5) в (1), получим:

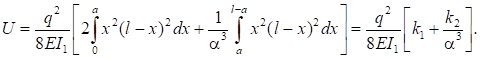
(7).

Коэффициенты и вычисляются следующим образом:

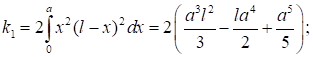
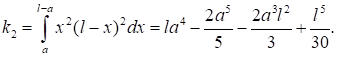
(8).

Оптимальное значение б найдем, продифференцировав ПЭД по б и приравняв к нулю:

(9).

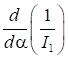
Производную вычислим как от сложной функции:

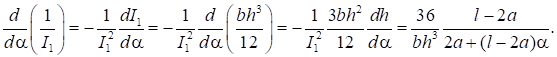
Окончательно задача сводится к следующему уравнению:

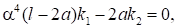
(10).

откуда.

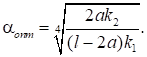
Из полученной формулы видно, что оптимальная величина параметра не зависит от ширины сечения. Следовательно, с ростом будет расти минимальный объем балки, необходимый для выполнения условия прочности. Таким образом, величину нужно назначать наименьшей из условия устойчивости плоской формы изгиба балки, либо из конструктивных соображений. Кроме того, не зависит от материала балки, а также величины нагрузки q.

На рис. 2 сплошной линией показан график изменения потенциальной энергии деформации балки переменного сечения U(б) по отношению к ПЭД балки постоянного объема U₀ в зависимости от при b = 10 см, a = 1 м, l = 6 м. Штриховой линии соответствует график изменения максимального прогиба балки f (б) по отношению к прогибу балки постоянного сечения f₀.

Минимуму потенциальной энергии деформации при указанных исходных данных соответствует. Балка, характеризующаяся минимумом ПЭД, обладает максимальной жесткостью при заданном объеме [1,2].

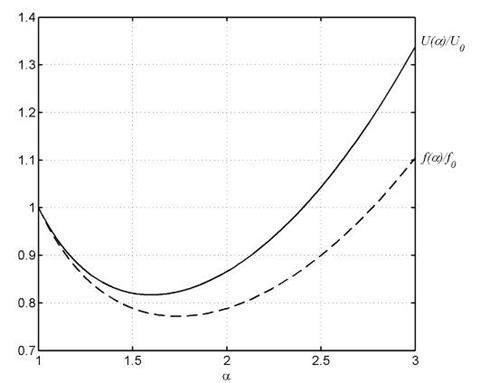
Рис. 2. — Изменение потенциальной энергии деформации и прогиба в середине пролета в зависимости от

Из рис. 2 видно, что относительно минимум прогиба смещен немного вправо. Это объясняется тем, что прогиб в середине пролета определяется умножением грузовой эпюры на единичную, а характер эпюры М₁ при действии равномерно распределенной нагрузки отличается от М_Р.

Отметим, что балка наибольшей жесткости не является равнопрочной.

При указанных исходных данных максимальные напряжения в крайних ступенях в 1.42 раза больше, чем в средней. Построение моделей равнопрочных балок и стержней рассматривается в работах [3−5]. Методики создания равнонапряженных конструкций приводятся в статьях [6−10].

Васильков Г. В. Теория адаптивной эволюции механических систем. Ростов н/Д: Терра-Принт, 2007. 248 с.

Васильков Г. В. Эволюционные задачи строительной механики: синергетическая парадигма. Ростов н/Д: ИнфоСервис, 2003. 179 с.

Барменкова Е.В., Андреев В. И. Изгиб двухслойной балки на упругом основании с учетом изменения жесткости балки по длине // International Journal for Computational Civil and Structural Engineering. 2011. Т. 7. № 3. С. 50−54.

Чепурненко А.С., Языев Б. М. Оптимизация формы поперечного сечения сжатых стержней из условия устойчивости // Научное обозрение. 2012. № 6. С. 202−204.

Чепурненко А.С., Андреев В. И., Языев Б. М. Построение модели равнопрочной многопролетной балки // Инженерный вестник Дона. 2013. № 1. URL: ivdon.ru/magazine/archive/n1y2013/1571.

Языев Б.М., Чепурненко А. С., Муханов А. В. Оптимизация толстостенной сферической оболочки на основе теории прочности Мора // Инженерный вестник Дона. 2013. № 3. URL: ivdon.ru/magazine/archive/n3y2013/1890.

Andreev V.I., Chepurnenko A.S., Jazyjev B.M. Model of Equal-stressed Cylinder based on the Mohr Failure Criterion //Advanced Materials Research Vols. 887−888 (2014) pp 869−872. Trans Tech Publications, Switzerland.

Чепурненко А.С., Андреев В. И., Языев Б. М. Построение модели равнонапряженного цилиндра на основе теории прочности Мора // Вестник МГСУ. 2013. № 5. С.56−61.

Andreev V.I., Avershyev A.S. Nonstationary problem moisture elasticity for a nonhomogeneous hollow thick-walled cylinder // WIT Transactions on the Built Environment. Fluid Structure Interaction VII. 2013. pр. 123−132.

Андреев В.И., Потехин И. А. О способе создания оптимальных конструкций на основе решения обратных задач теории упругости неоднородных тел // Вестник Отделения строительных наук Российской академии архитектуры и строительных наук. 2007. № 11. С. 48−52.

References.

Vasil’kov G.V. Teoriya adaptivnoy evolyutsii mekhanicheskikh system [The theory of adaptive evolution of mechanical systems]. Rostov n/D: Terra-Print, 2007. 248 p.

Vasil’kov G.V. Evolyutsionnye zadachi stroitel’noy mekhaniki: sinergeticheskaya paradigma [Evolutional problems of structural mechanics: synergetic paradigm]. Rostov n/D: InfoServis, 2003. 179 p.

Barmenkova E.V., Andreev V.I. International Journal for Computational Civil and Structural Engineering. 2011. T. 7. № 3. pp. 50−54.

Chepurnenko A.S., Yazyev B.M. Nauchnoe obozrenie. 2012. № 6. pp. 202−204.

Chepurnenko A.S., Andreev V.I., Yazyev B.M. Inћenernyj vestnik Dona (Rus). 2013. № 1. URL: ivdon.ru/magazine/archive/n1y2013/1571.

Yazyev B.M., Chepurnenko A.S., Mukhanov A.V. Inћenernyj vestnik Dona (Rus). 2013. № 3. URL: ivdon.ru/magazine/archive/n3y2013/1890.

Andreev V.I., Chepurnenko A.S., Jazyjev B.M. Advanced Materials Research Vols. 887−888 (2014) pp 869−872. Trans Tech Publications, Switzerland.

Chepurnenko A.S., Andreev V.I., Yazyev B.M. Vestnik MGSU. 2013. № 5. pp.56−61.

Andreev V.I., Avershyev A.S. WIT Transactions on the Built Environment. Fluid Structure Interaction VII. 2013. pp. 123−132.

Andreev V.I., Potekhin I.A. Vestnik Otdeleniya stroitel’nykh nauk Rossiyskoy akademii arkhitektury i stroitel’nykh nauk. 2007. № 11. pp. 48−52.