Пример иерархического кластерного анализа

Пусть имеется шесть объектов. Каждый объект описывается двумя показателями. Исходная матрица наблюдений X имеет вид:

Используя в качестве метрики квадрат Евклидова расстояния, получаем матрицу расстояний:

Применим для образования кластеров метод одиночной связи и метод ближайшего соседа.

• 1. Объединяем объекты первый и шестой (расстояние равно 1) в первый кластер.
• 2. Объединяем объекты второй и четвертый (расстояние равно 1) во второй кластер.
• 3. Включаем в первый кластер третий объект, так как расстояние между ним и первым объектом минимально (равно 2).
• 4. Включаем во второй кластер пятый объект, так как расстояние между ним и четвертым объектом минимально (равно 2).
• 5. Объединяем первый и второй кластеры, так как расстояние между вторым и третьим объектом минимально (равно 4).

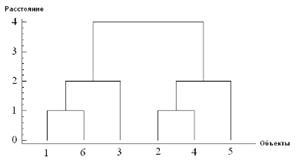
Последовательность объединения графически представляется в виде графа-дерева (дендрограммы):

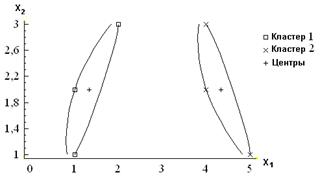
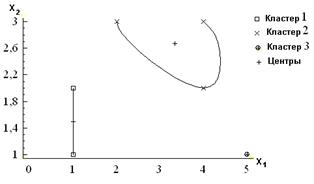
Ниже на рисунке в плоскости x₁, x₂ показаны первый и второй кластеры.

Необходимо отметить, что результат классификации зависит как от метода классификации и применяемой метрики, так и от нормализации (стандартизации) значений признаков. Например, при решении данной задачи признаки имели естественные значения. Если выполнить нормализацию исходных данных, то матрица Z будет иметь вид:

Напомним, что.

z_il = (x_il — x_l) /S_l,.

где x_il — значение l-го признака i-го объекта;

x_l — среднее арифметическое значение l-го признака;

S_l = (?_i (x_il — x_l) ²/ (n-1)) ^½ — стандартное отклонение l-го признака.

В нашем случае x₁ = 2,83, S₁ = 1,72, x₂ = 2,0, S₂ = 0,89.

Матрица расстояний имеет вид:

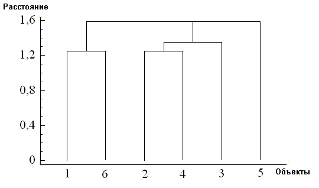
Применение тех же методов одиночной связи и ближайшего соседа получаем другое разбиение на кластеры:

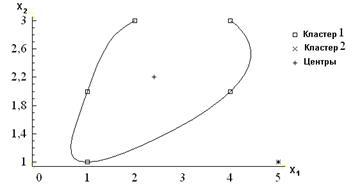
Отдельным кластером является пятый объект. В плоскости x₁, x₂ показаны первый и второй кластеры.

Однако из дендрограммы очевидно, что удачнее разбиение на три кластера:

Кластер 1: объекты 1 и 6; кластер 2: объекты 2, 3 и 4; кластер 3: объект Таким образом, выделяют две группы методов кластерного анализа: иерархические и неиерархические.

Основными методами иерархического кластерного анализа являются метод ближнего соседа, метод полной связи, метод средней связи и метод Варда. Наиболее универсальным является последний.