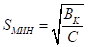Проверка кабелей на термическую стойкость

Выбранные в нормальном режиме и проверенные по допустимой перегрузке в послеаварийном режиме кабели проверяются по условию.

S_МИН.? S_Э, (1.35).

где S_МИН — минимальное сечение по термической стойкости, мм²; S_Э — экономическое сечение, мм², определенное по формуле (1.34).

При этом кабели небольшой длины проверяются по току при коротком замыкании в начале кабеля; одиночные кабели со ступенчатым сечением по длине проверяют по току К.З. в начале каждого участка. Два параллельных кабеля и более проверяют по токам К.З. непосредственно за пучком кабелей, т. е. с учетом разветвления тока К.З.

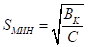
(1.36).

где В_К — импульс квадратичного тока К.З. (тепловой импульс тока К.З.),.

А² · с; С — функция, значения которой приведены в табл.1.26 [17], А · с^½/мм².

Тепловой импульс тока определяется В_К = I²_П.О. · (t_Р.З. + t_В +T_А), (1.37).

где I_П.О — начальное значение периодической составляющей тока К.З., А; t_Р.З — время действия релейной защиты, с. Принимается t_Р.З = 2 с. — для питающих сетей; t_Р.З = 0,5 с. — для распределительных сетей [16]; t_В — полное время отключения выключателя, с. В зависимости от типа выключателя t_В = 0,04−0,2 с.; T_А — постоянная времени затухания апериодической составляющей тока короткого замыкания, с. Для распределительных сетей напряжением 6−10 кВ Т_А = 0,01 с. [17].