Учёт влияния отличия модулей упругости на сжатие и растяжение при расчёте на прочность армированных балок с заполнителем из фибропенобетона

При расчёте железобетонных балок рекомендуется рассчитывать их по предельным состояниям, считая, что во всей растянутой зоне нормальные растягивающие напряжения достигли предельного разрушающего значения [1]. Далее расчёт на прочность железобетонной балки проводится с учётом только сжатой зоны [2]. При этом считается, что модули упругости на растяжение и модуль упругости при сжатии одинаковы. На самом деле для некоторых видов бетона, например для фибропенобетона, [3].

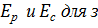
Целью данной работы является выяснить как влияет на прочность армированных балок учет отличия заполнителя [4,5].

Рассмотрим армированную бетонную балку произвольного поперечного сечения, произвольно опёртую и произвольно нагруженную изгибающими нагрузками, вызывающими плоский изгиб.

Обозначим:

— изгибающий момент относительно нейтральной линии в произвольном поперечном сечении балки,.

n — число стержней арматуры,.

• — осевой момент инерции поперечного сечения одного стержня арматуры,
• — изгибающий момент, возникающий в одном стержне арматуры,

— модуль упругости при растяжении стержней арматуры,.

— изгибающий момент, возникающий в бетонной части балки,.

— изгибающий момент, возникающий в растягивающей части бетона,.

— модуль упругости бетона (заполнителя) при растяжении,.

— осевой момент инерции растягивающей части бетона,.

• — изгибающий момент, возникающий в сжимающей части бетона,
• — модуль упругости бетона (заполнителя) при сжатии,
• — осевой момент инерции сжимающей части бетона.

Найдём формулы для определения изгибающих моментов, возникающих в стержнях арматуры, сжатой и растянутой части бетона (заполнителя) [6]. Используя методы сопротивления материаловимеем следующую зависимость между изгибающими моментами [7,8].

где, (1).

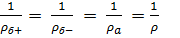
(2), где.

— радиус кривизны растянутой зоны заполнителя (бетона),.

— радиус кривизны сжатой зоны заполнителя (бетона),.

— радиус кривизны стержня арматуры,.

— радиус кривизны балки.

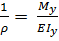
Формула радиуса кривизны имеет вид. Соответственно.

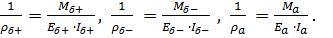
(3).

Подставив (3) в (1), (2), получим:

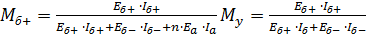
(4).

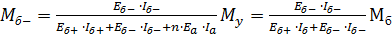
(5).

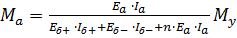
. (6).

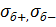
Найдём зависимость между нормальными напряжениями, возникающими в растягивающей и сжимающей зоне заполнителя (бетона) и соответствующими изгибающими моментами [9].

Для заполнителей, у которых верен закон Гука, можно использовать известные зависимости (7), (8) при выводе нормальных напряжений железобетонный балка изгибающий.

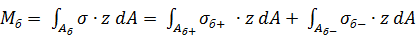
. (7).

Где, — площади поперечного сечения растянутой и сжимающей зоны заполнителя.

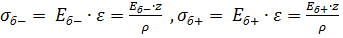
. (8).

Подставив (8) в (7), найдём выражение для радиуса кривизны нейтрального слоя:

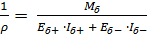
. (9).

Найдём выражения нормальных напряжений, возникающих в заполнителе, подставив (8) в (9).

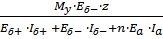
= =, (10).

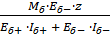
= =, (11).

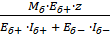
Где z — расстояние от нейтральной линии 0y до точки, в которой определяется нормальное напряжение [10].

Для определения положения нейтральной линии воспользуемся условием:

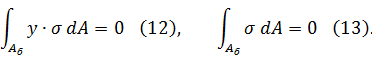
Подставив (10), (11) в (12), получим выражение.

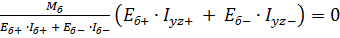
и из этого выражения получаем формулу для определения положения нейтральной линии.

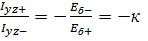
(14).

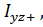
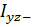
Где — центробежные моменты инерции относительно произвольных осей, но ось 0y перпендикулярна плоскости действия приложенных нагрузок.

Рассмотрим условие (13).

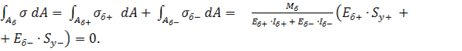
(15).

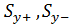
Где — статические моменты инерции относительно нейтральной линии, совпадающей с осью 0y.

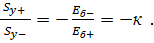
Для определения положения нейтральной линии из выражения (15) получаем: (16).

Если ось 0z является главной осью, то условие (14) удовлетворяется тождественно и положение нейтральной линии определяется из условия (16).

Используя условие (16) и формулы (10),(11), найдём положение нейтральной линии и выражения максимальных растягивающих и сжимающих напряжений для армированных балок прямоугольного поперечного сечения:

.

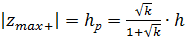
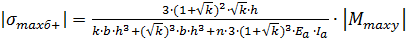
(17).

.

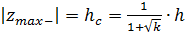
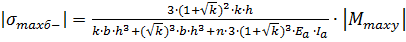
. (18).

Гдевысота растягивающейся зоны, — высота сжимающейся зоны,.

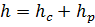
высота прямоугольного поперечного сечения балки.

Используя формулы (17), (18) для максимальных нормальных напряжений можно проводить расчёт на прочность, как по допускаемым напряжениям, так и по предельным состояниям армированных балок прямоугольного поперечного сечения с любыми заполнителями, материал которых следует закону Гука. Таким требованиям, например, отвечает фибропенобетон.

• 1. Андреев В. И., Языев Б. М. Выпучивание продольно сжатых стержней переменной жесткости при ползучести// Инженерный вестник Дона, вып. 4(ч.2), 2012
• 2. Н. А. Бескопыльный, М. И. Кадомцев, А. А. Ляпин Методика исследования динамических воздействий на перекрытия пешеходного перехода при проезде транспорта // Инженерный вестник Дона, вып. 4, 2011
• 3. Моргун Л. В., Смирнова П. В., Моргун В. Н., Богатина А. Ю. Конструкционные возможности фибропенобетона неавтоклавного твердения// Ж. «Строительные материалы», 2012, № 4. — С.14…16.
• 4. Филин А. П. Прикладная механика твёрдого деформируемого тела. Т.1. — М. изд-во" Наука", Гл. ред. физ.-мат. литературы, 1981.-832 с.
• 5. Кадомцева Е. Э. Прочность при ударе по составной балке. «Строительство 2009», Материалы юбилейной международной научнопрактической конференции/Ростовский государственный строительный университет — Ростов-на-Дону: редакционно-издательский центр РГСУ, 2009.-228с.
• 6. Чепурненко А. С., Языев Б. М. Оптимизация формы поперечного сечения сжатых стержней из условия устойчивости//Научное обозрение. 2012. № 6. — С. 45−49.
• 7. Fabrikant V.I. Applications of Potential Theory in Mechanics. Selection of New Results. Kluwer, 1989 (djvu)
• 8. Fabrikant V.I. Mixed Boundary Value Problems of Potential Theory and thА. eir Applications in Engineering. Kluwer, 1991 (djvu)
• 9. Чепуренко А. С., Андреев В. И., Языев Б. М. Построение модели равнопрочной многопролётной балки // Инженерный вестник Дона, вып. 1, 2013