Математическая модель АСК-анализа

Количественная мера знаний

Математический метод АСК-анализа основан на системной теории информации (СТИ), которая создана в рамках реализации программной идеи обобщения всех понятий математики, в частности теории информации, базирующихся на теории множеств, путем тотальной замены понятия множества на более общее понятие системы и тщательного отслеживания всех последствий этой замены [3, 5]. Благодаря математическому методу, положенному в основу АСК-анализа, этот метод является непараметрическим и позволяет в реализующей его системе «Эйдос-Х++» сопоставимо обрабатывать десятки и сотни тысяч градаций факторов и будущих состояний нелинейных [19] многопараметрических объектов управления (классов) при неполных (фрагментированных), зашумленных данных числовой и нечисловой природы измеряемых в различных единицах измерения [3, 5].

Итак, будем считать, что информация содержится не только в самих базовых элементах системы, но и в ее подсистемах различной сложности, т. е. состоящих из 2, 3,… m,… M базовых элементов.

Классическая формула Хартли имеет вид [3]:

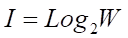
Будем искать ее системное обобщение в виде [3]:

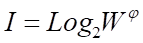
где:

W — количество элементов в множестве.

I — количество информации, которое содержится в факте извлечения одного элемента из множества.

— коэффициент эмерджентности, названный автором в честь Р. Хартли, коэффициентом эмерджентности Хартли.

Суммарное количество таких подсистем для систем, подчиняющихся статистике Ферми-Дирака [20, 21], можно принять равным числу сочетаний. Поэтому примем, что системное обобщение формулы Хартли имеет вид:

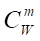
— количество подсистем из m элементов;

m — сложность подсистем;

M — максимальная сложность подсистем (максимальное число элементов подсистемы).

Так как, то при M=1 система переходит в множество и выражение (3) приобретает вид (1), т. е. для него выполняется принцип соответствия, являющийся обязательным для более общей теории.

Учитывая, что при M=W:

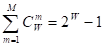
в этом случае получаем:

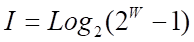
Выражение (5) дает оценку максимального количества информации в элементе системы. Из выражения (5) видно, что при увеличении числа элементов W количество информации I быстро стремится к W (6) и уже при W>4 погрешность выражения (5) не превышает 1%:

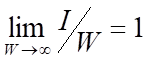
Приравняв правые части выражений (2) и (3):

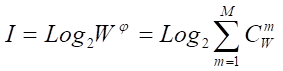
получим выражение для коэффициента эмерджентности Хартли:

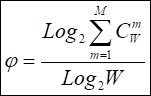
Смысл этого коэффициента весьма интересен и раскрыт в работах [3, 15] и ряде других. Здесь отметим лишь, что при M1, когда система асимптотически переходит в множество, имеем 1 и (2) (1), как и должно быть согласно принципу соответствия, предложенному Нильсом Бором в 1913 году.

С учетом (8) выражение (2) примет вид:

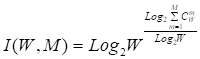
или при M=W и больших W, учитывая (4) и (5):

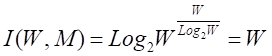
Выражение (9) и представляет собой искомое системное обобщение классической формулы Хартли, а выражение (10) — его достаточно хорошее приближение при большом количестве элементов в системе W.

Классическая формула А. Харкевича имеет вид:

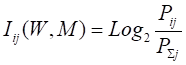
где: — Pij — условная вероятность перехода объекта в j-е состояние при условии действия на него i-го значения фактора;

— - безусловная вероятность перехода объекта в j-е состояние (вероятность самопроизвольного перехода или вероятность перехода, посчитанная по всей выборке, т. е. при действии любого значения фактора).

Придадим выражению (11) следующий эквивалентный вид (12), который и будем использовать ниже. Вопрос об эквивалентности выражений (11) и (12) рассмотрим позднее.

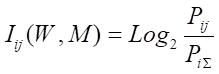
где: — индекс i обозначает признак (значение фактора): 1 i M;

• — индекс j обозначает состояние объекта или класс: 1 j W;
• — Pij — условная вероятность наблюдения i-го значения фактора у объектов в j-го класса;
• — - безусловная вероятность наблюдения i-го значения фактора по всей выборке.

Из (12) видно, что формула Харкевича для семантической меры информации по сути является логарифмом от формулы Байеса для апостериорной вероятности (отношение условной вероятности к безусловной).

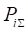
Известно, что классическая формула Шеннона для количества информации для неравновероятных событий преобразуется в формулу Хартли при условии, что события равновероятны, т. е. удовлетворяет фундаментальному принципу соответствия. Поэтому теория информации Шеннона справедливо считается обобщением теории Хартли для неравновероятных событий. Однако, выражения (11) и (12) при подстановке в них реальных численных значений вероятностей Pij, и не дает количества информации в битах, т. е. для этого выражения не выполняется принцип соответствия, обязательный для более общих теорий. Возможно, в этом состоит причина довольно сдержанного, а иногда и скептического отношения специалистов по теории информации Шеннона к семантической теории информации Харкевича.

Причину этого мы видим в том, что в выражениях (11) и (12) отсутствуют глобальные параметры конкретной модели W и M, т. е. в том, что А. Харкевич в своем выражении для количества информации не ввел зависимости от мощности пространства будущих состояний объекта W и количества значений факторов M, обуславливающих переход объекта в эти состояния.

Поставим задачу получить такое обобщение формулы Харкевича, которое бы удовлетворяло тому же самому принципу соответствия, что и формула Шеннона, т. е. преобразовывалось в формулу Хартли в предельном детерминистском равновероятном случае, когда каждому классу (состоянию объекта) соответствует один признак (значение фактора), и каждому признаку — один класс, и эти классы (а значит и признаки) равновероятны, и при этом каждый фактор однозначно, т. е. детерминистским образом определяет переход объекта в определенное состояние, соответствующее классу.

В детерминистском случае вероятность Pij наблюдения объекта j-го класса при обнаружении у него i-го признака:

.

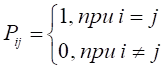
Будем искать это обобщение (12) в виде:

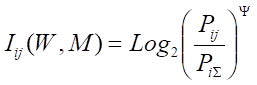
Найдем такое выражение для коэффициента, названного автором в честь А. Харкевича «коэффициентом эмерджентности Харкевича», которое обеспечивает выполнение для выражения (13) принципа соответствия с классической формулой Хартли (1) и ее системным обобщением (2) и (3) в равновероятном детерминистском случае.

Для этого нам потребуется выразить вероятности Pij, Pj и Pi через частоты наблюдения признаков по классам.