Математическая модель бизнес-процесса оформления групповых заявок от юридических лиц на посещение парка развлечений ООО «Сказка-град»

Отобразим выделенную проблему в виде математической модели.

В качестве математической модели выступает Сеть Петри [2] -математический аппарат для моделирования динамических дискретных систем, в том числе и информационных систем, ориентированная на качественный анализ и синтез таких систем.

Процесс обслуживания клиента при продаже услуг представляется в виде последовательного процесса действий, с некоторыми задержками во времени. В каждой позиции содержится одна метка, которая переходит из состояния в состояние.

Сеть Петри задается в виде набора, где Р и Т — конечные множества позиций и переходов, I и Омножества входных и выходных функций.

Зададим сеть Петри для нашего процесса:

P = {p1, p2, p3, p4, p5, p6, p7, p8, p9, p10} - множество состояний процесса;

T = {t1, t 2, t3, t4, t5, t6, t7, t8, t9} -множество переходов процесса;

I = {i1, i2, i3, i4, i5, i6, i7, i8, i9} - множество входных функций;

O = {o1, o2, o3, o4, o5, o6, o7} -множество выходных функций.

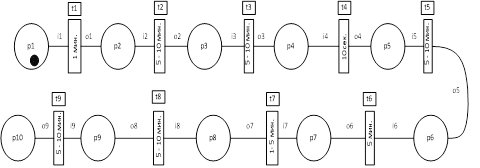
Математическая модель процесса обслуживания клиента при продаже услуг в отделе продаж представлена на рисунке 1.7.

Рисунок 1.7. — Граф сети Петри для процесса оформления групповой заявки на посещение парка развлечений ООО «Сказка-град» на текущий момент Таблица 1.1- Значения событий и переходов.

Мною было проведено оценивание временных затрат на выполнение бизнес-процессов с применением методов наблюдения и анкетирования. По результатам оценивания были получены следующие значения (см. табл. 1.2).

Таблица 1.2 — Временные оценки.

После подготовки рекламной кампании отдел готов к приему клиентов на обслуживание.

При приеме клиента менеджер консультирует его об условиях посещения парка развлечений. Консультация занимает обычно от 5 до 10 минут.

После проведения консультации клиент оформляет заявление с указанием выбранных аттракционов (5 — 10 минут).

Отдел продаж рассматривает заявление (5 — 10 минут), передает данные в службу расчетов, которая выставляет счет за выбранные услуги (5 минут).

Клиент счет оплачивает, после чего заключается договор на обслуживание (5 — 10 минут). По заключению договора группа от юридического лица, на кого оформлен договор, посещает парк развлечений. Таким образом, процесс обслуживания клиента может занять от часа до полутора часа.