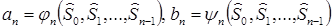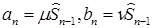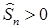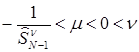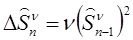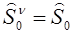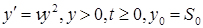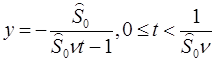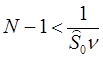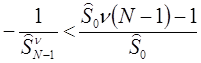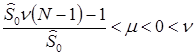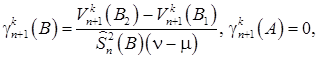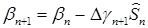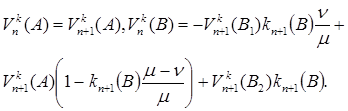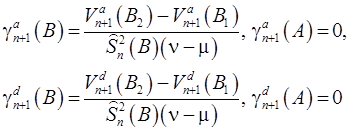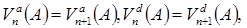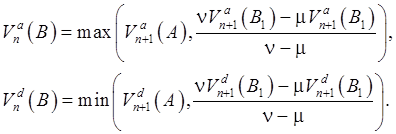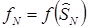Модель с динамически изменяющимися параметрами

Начнем изложение с определения.

Определение. [Ширяев]. Последовательность удовлетворяет условию условного двуточия, если, где. При этом утверждения:

• 1) безарбитражныйрынок является полным;
• 2) дисконтированная стоимость акции удовлетворяет условию условного двуточия и ;

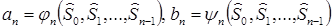
являются эквивалентными.

Основным источником случайности нарынке считается рисковый актив. Поскольку рассматривается дискретныйрынок, то эквивалентно. Наиболее простой случай, когда.

.(3.24).

Так как, то из неравенств: следует, что.

.(3.25).

В (3.25) последовательность удовлетворяет разностному уравнению:

.

.

Отметим, что данное разностное уравнение является эйлеровой аппроксимацией дифференциального уравнения:, решением которого является функция.

.

Поскольку решение — выпуклая функция, то при.

.

справедливо неравенство.

.

В этом случае вместо неравенств (3.25), можно рассматривать более грубые неравенства:

. (3.26).

Применим формулы (3.17). Отметим, что.

.

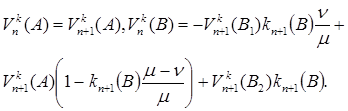
(3.27).

Отсюда для вычисления верхней и нижней цен, а также верхнего и нижнего хеджа получаем формулы:

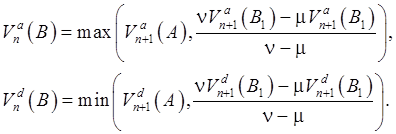
(3.28).

Случай, когда дисконтированное финансовое обязательство.

— выпуклая функция, предлагаем рассмотреть читателю.