Алгоритм обратного распространения ошибки

• Введение
• Глава 1. Обучение нейронных сетей
• 1.1 Общие подходы нейронных сетей
• Глава 2. Алгоритм обратного распространения ошибки
• 2.1 Описание алгоритма обратного распространения ошибки
• 2.2 Реализация алгоритма обратного распространения ошибки на примере аппроксимации функции
• 2.3 Анализ алгоритма обратного распространения ошибки
• Список использованной литературы

В последние несколько лет мы наблюдаем взрыв интереса к нейронным сетям, которые успешно применяются в самых различных областях — бизнесе, медицине, технике, геологии, физике. Нейронные сети вошли в практику везде, где нужно решать задачи прогнозирования, классификации или управления. Такой впечатляющий успех определяется несколькими причинами:

Богатые возможности. Нейронные сети — исключительно мощный метод моделирования, позволяющий воспроизводить чрезвычайно сложные зависимости.

Простота в использовании. Нейронные сети учатся на примерах. Пользователь нейронной сети подбирает представительные данные, а затем запускает алгоритм обучения, который автоматически воспринимает структуру данных. При этом от пользователя, конечно, требуется какой-то набор эвристических знаний о том, как следует отбирать и подготавливать данные, выбирать нужную архитектуру сети и интерпретировать результаты, однако уровень знаний, необходимый для успешного применения нейронных сетей, гораздо скромнее, чем, например, при использовании традиционных методов статистики.

Нейронные сети привлекательны с интуитивной точки зрения, ибо они основаны на примитивной биологической модели нервных систем. В будущем развитие таких нейробиологических моделей может привести к созданию действительно мыслящих компьютеров.

Области применения нейронных сетей весьма разнообразны — это распознавание текста и речи, семантический поиск, экспертные системы и системы поддержки принятия решений, предсказание курсов акций, системы безопасности, анализ текстов. В данной курсовой работе рассматривается пример использования нейронной сети для аппроксимации функции.

алгоритм нейронная сеть ошибка Цель работы — изучение алгоритмов обратного распространения ошибки.

Для достижения поставленной цели в работе поставлены следующие задачи:

1. Изучить общие подходы обучения нейронных сетей.

2. Рассмотреть переобучение и обобщение.

3. Рассмотреть алгоритм обратного распространения ошибки.

4. Реализовать алгоритм обратного распространения ошибки на примере аппроксимации функции.

Объектом исследования являются нейронные сети.

Предмет — алгоритм обратного распространения ошибки.

Практической значимостью работы является возможность использования алгоритма обратного распространения ошибки для решения различных задач.

Структура работы и объем работы определяется целью и основными задачами исследования. Курсовая работа состоит из введения, двух глав, заключения и списка использованной литературы. Текст работы изложен на 33 страницах текста.

Глава 1. Обучение нейронных сетей

1.1 Общие подходы нейронных сетей

Самым важным свойством нейронных сетей является их способность обучаться на основе данных окружающей среды и в результате обучения повышать свою производительность. Повышение производительности происходит со временем в соответствии с определенными правилами. Обучение нейронной сети происходит посредством интерактивного процесса корректировки синаптических весов и порогов. В идеальном случае нейронная сеть получает знания об окружающей среде на каждой итерации процесса обучения.

С понятием обучения ассоциируется довольно много видов деятельности, поэтому сложно дать этому процессу однозначное определение. Более того, процесс обучения зависит от точки зрения на него. Именно это делает практически невозможным появление какого-либо точного определения этого понятия. Например, процесс обучения с точки зрения психолога в корне отличается от обучения с точки зрения школьного учителя. С позиций нейронной сети, вероятно, можно использовать следующее определение:

Обучение — это процесс, в котором свободные параметры нейронной сети настраиваются посредством моделирования среды, в которую эта сеть встроена. Тип обучения определяется способом подстройки этих параметров.

Это определение процесса обучения нейронной сети предполагает следующую последовательность событий:

1. В нейронную сеть поступают стимулы из внешней среды.

2. В результате первого пункта изменяются свободные параметры нейронной сети.

3. После изменения внутренней структуры нейронная сеть отвечает на возбуждения уже иным образом.

Вышеуказанный список четких правил решения проблемы обучения нейронной сети называется алгоритмом обучения. Несложно догадаться, что не существует универсального алгоритма обучения, подходящего для всех архитектур нейронных сетей. Существует лишь набор средств, представленный множеством алгоритмов обучения, каждый из которых имеет свои достоинства. Алгоритмы обучения отличаются друг от друга способом настройки синаптических весов нейронов. Еще одной отличительной характеристикой является способ связи обучаемой нейронной сети с внешним миром. В этом контексте говорят о парадигме обучения, связанной с моделью окружающей среды, в которой функционирует данная нейронная сеть.

Существуют два концептуальных подхода к обучению нейронных сетей: обучение с учителем и обучение без учителя.

Обучение нейронной сети с учителем предполагает, что для каждого входного вектора из обучающего множества существует требуемое значение выходного вектора, называемого целевым. Эти вектора образуют обучающую пару. Веса сети изменяют до тех пор, пока для каждого входного вектора не будет получен приемлемый уровень отклонения выходного вектора от целевого.

Обучение нейронной сети без учителя является намного более правдоподобной моделью обучения с точки зрения биологических корней искусственных нейронных сетей. Обучающее множество состоит лишь из входных векторов. Алгоритм обучения нейронной сети подстраивает веса сети так, чтобы получались согласованные выходные векторы, т. е. чтобы предъявление достаточно близких входных векторов давало одинаковые выходы.

1.2 Переобучение и обобщение.

Одна из наиболее серьезных трудностей изложенного подхода заключается в том, что таким образом мы минимизируем не ту ошибку, которую на самом деле нужно минимизировать, — ошибку, которую можно ожидать от сети, когда ей будут подаваться совершенно новые наблюдения. Иначе говоря, мы хотели бы, чтобы нейронная сеть обладала способностью обобщать результат на новые наблюдения. В действительности сеть обучается минимизировать ошибку на обучающем множестве, и в отсутствие идеального и бесконечно большого обучающего множества это совсем не то же самое, что минимизировать «настоящую» ошибку на поверхности ошибок в заранее неизвестной модели явления (Bishop, 1995).

Сильнее всего это различие проявляется в проблеме переобучения, или слишком близкой подгонки. Это явление проще будет продемонстрировать не для нейронной сети, а на примере аппроксимации посредством полиномов, — при этом суть явления абсолютно та же.

Полином (или многочлен) — это выражение, содержащее только константы и целые степени независимой переменной. Вот примеры:

y=2x+3 y=3x²+4x+1

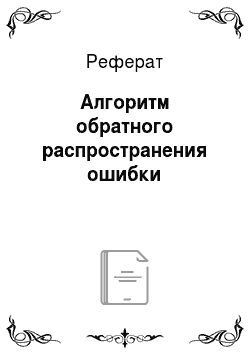
Графики полиномов могут иметь различную форму, причем чем выше степень многочлена (и, тем самым, чем больше членов в него входит), тем более сложной может быть эта форма. Если у нас есть некоторые данные, мы можем поставить цель подогнать к ним полиномиальную кривую (модель) и получить таким образом объяснение для имеющейся зависимости. Наши данные могут быть зашумлены, поэтому нельзя считать, что самая лучшая модель задается кривой, которая в точности проходит через все имеющиеся точки. Полином низкого порядка может быть недостаточно гибким средством для аппроксимации данных, в то время как полином высокого порядка может оказаться чересчур гибким, и будет точно следовать данным, принимая при этом замысловатую форму, не имеющую никакого отношения к форме настоящей зависимости (см. рис. 1).

Рис 1 — График полинома Нейронная сеть сталкивается с точно такой же трудностью. Сети с большим числом весов моделируют более сложные функции и, следовательно, склонны к переобучению. Сеть же с небольшим числом весов может оказаться недостаточно гибкой, чтобы смоделировать имеющуюся зависимость. Например, сеть без промежуточных слоев на самом деле моделирует обычную линейную функцию.

Как же выбрать «правильную» степень сложности для сети? Почти всегда более сложная сеть дает меньшую ошибку, но это может свидетельствовать не о хорошем качестве модели, а о переобучении.

Ответ состоит в том, чтобы использовать механизм контрольной кросс-проверки. Мы резервируем часть обучающих наблюдений и не используем их в обучении по алгоритму обратного распространения. Вместо этого, по мере работы алгоритма, они используются для независимого контроля результата. В самом начале работы ошибка сети на обучающем и контрольном множестве будет одинаковой (если они существенно отличаются, то, вероятно, разбиение всех наблюдений на два множества было неоднородно). По мере того, как сеть обучается, ошибка обучения, естественно, убывает, и, пока обучение уменьшает действительную функцию ошибок, ошибка на контрольном множестве также будет убывать. Если же контрольная ошибка перестала убывать или даже стала расти, это указывает на то, что сеть начала слишком близко аппроксимировать данные и обучение следует остановить (в пакете ST Neural Networks можно задать автоматическую остановку обучения при появлении эффекта переобучения). Это явление чересчур точной аппроксимации в процессе обучения и называется переобучением. Если такое случилось, то обычно советуют уменьшить число скрытых элементов и/или слоев, ибо сеть является слишком мощной для данной задачи. Если же сеть, наоборот, была взята недостаточно богатой для того, чтобы моделировать имеющуюся зависимость, то переобучения, скорее всего, не произойдет, и обе ошибки — обучения и проверки — не достигнут достаточного уровня малости.

Описанные проблемы с локальными минимумами и выбором размера сети приводят к тому, что при практической работе с нейронными сетями, как правило, приходится экспериментировать с большим числом различных сетей, порой обучая каждую из них по нескольку раз (чтобы не быть введенным в заблуждение локальными минимумами) и сравнивая полученные результаты. Главным показателем качества результата является здесь контрольная ошибка. При этом, в соответствии с общенаучным принципом, согласно которому при прочих равных следует предпочесть более простую модель, из двух сетей с приблизительно равными ошибками контроля имеет смысл выбрать ту, которая меньше.

Необходимость многократных экспериментов ведет к тому, что контрольное множество начинает играть ключевую роль в выборе модели, то есть становится частью процесса обучения. Тем самым ослабляется его роль как независимого критерия качества модели — при большом числе экспериментов есть риск выбрать «удачную» сеть, дающую хороший результат на контрольном множестве. Для того, чтобы придать окончательной модели должную надежность, часто (по крайней мере, когда объем обучающих данных это позволяет) поступают так: резервируют еще одно — тестовое множество наблюдений. Итоговая модель тестируется на данных из этого множества, чтобы убедиться, что результаты, достигнутые на обучающем и контрольном множествах реальны, а не являются артефактами процесса обучения. Разумеется, для того чтобы хорошо играть свою роль, тестовое множество должно быть использовано только один раз: если его использовать повторно для корректировки процесса обучения, то оно фактически превратится в контрольное множество.

Итак, построение сети (после выбора входных переменных) состоит из следующих шагов:

· Выбрать начальную конфигурацию сети (например, один промежуточный слой с числом элементов в нем, равным полусумме числа входов и числа выходов — Наставник (Network Advisor) пакета ST Neural Networks предложит Вам такую конфигурацию по умолчанию).

· Провести ряд экспериментов с различными конфигурациями, запоминая при этом лучшую сеть (в смысле контрольной ошибки). В пакете ST Neural Networks предусмотрено автоматическое запоминание лучшей сети во время эксперимента. Для каждой конфигурации следует провести несколько экспериментов, чтобы не получить ошибочный результат из-за того, что процесс обучения попал в локальный минимум.

· Если в очередном эксперименте наблюдается недообучение (сеть не выдает результат приемлемого качества), попробовать добавить дополнительные нейроны в промежуточный слой (слои). Если это не помогает, попробовать добавить новый промежуточный слой.

· Если имеет место переобучение (контрольная ошибка стала расти), попробовать удалить несколько скрытых элементов (а возможно и слоев).

Многократное повторение эвристических экспериментов в лучшем случае довольно утомительно, и поэтому в пакет ST Neural Networks включен специальный алгоритм автоматического поиска, который проделает эти действия за Вас. Автоматический конструктор сети - Automatic Network Designer проведет эксперименты с различным числом скрытых элементов, для каждой пробной архитектуры сети выполнит несколько прогонов обучения, отбирая при этом наилучшую сеть по показателю контрольной ошибки с поправкой на размер сети. В Автоматическом конструкторе сети реализованы сложные алгоритмы поиска, в том числе метод «искусственного отжига» (simulated annealing, Kirkpatrick et al., 1983), с помощью которых можно перепробовать сотни различных сетей, выделяя из них особо перспективные, либо быстро находить «грубое и простое» решение.

Глава 2. Алгоритм обратного распространения ошибки

2.1 Описание алгоритма обратного распространения ошибки

Строго говоря, метод обратного распространения ошибки — это способ быстрого расчета градиента, основанный на особенностях функции пересчета сети, которые позволяют сократить вычислительную сложность расчета градиента. Метод использует ошибку на выходе сети для расчета частных производных по весам последнего слоя обучаемых связей, затем по весам последнего слоя и ошибке сети определяется ошибка на выходе предпоследнего слоя и процесс повторяется.

Описание алгоритма

Обратное распространение ошибки применяется к многослойным сетям, нейроны которых имеют нелинейность с непрерывной производной, например такую:

Нелинейность такого вида удобна простотой расчета производной:

Для обучения сети используется P пар векторов сигналов: входной вектор I и вектор, который должен быть получен на выходе сети D. Сеть, в простом случае, состоит из N слоев, причем каждый нейрон последующего слоя связан со всеми нейронами предыдущего слоя связями, с весами w ^[n].

При прямом распространении, для каждого слоя рассчитывается (и запоминается) суммарный сигнал на выходе слоя (S ^[n]) и сигнал на выходе нейрона. Так, сигнал на входе i-го нейрона n-го слоя:

Здесь w (_{i, j) —} веса связей n-го слоя. Сигнал на выходе нейрона рассчитывается применением к суммарному сигналу нелинейности нейрона.

Сигнал выходного слоя x ^[N] считается выходным сигналом сети O.

По выходному сигналу сети O и сигналу D, который должен получится на выходе сети для данного входа, рассчитываться ошибка сети. Обычно используется средний квадрат отклонения по всем векторам обучающей выборки:

Для обучения сети используется градиент функции ошибки по весам сети. Алгоритм обратного распространения предполагает расчет градиента функции ошибки «обратным распространением сигнала» ошибки. Тогда частная производная ошибки по весам связей рассчитывается по формуле:

Здесь д — невязка сети, которая для выходного слоя рассчитывается по функции ошибки:

А для скрытых слоев — по невязке предыдущего слоя:

Для случая сигмоидной нелинейности и среднего квадрата отклонения как функции ошибки:

Собственно обучение сети состоит в нахождении таких значений весов, которые минимизируют ошибку на выходах сети. Существует множество методов, основанных или использующих градиент, позволяющих решить эту задачу. В простейшем случае, обучение сети проводится при помощи небольших приращений весов связей в направлении, противоположенном вектору градиента:

Такой метод обучения называется «оптимизация методом градиентного спуска» и, в случае нейросетей, часто считается частью метода обратного распространения ошибки.

2.2 Реализация алгоритма обратного распространения ошибки на примере аппроксимации функции

Задание: Пусть имеется таблица значений аргумента (x_i) и соответствующих значений функции (f (x_i)) (эта таблица могла возникнуть при вычислениях некоторой аналитически заданной функции при проведении эксперимента по выявлению зависимости силы тока от сопротивления в электрической сети, при выявлении связи между солнечной активностью и количеством обращений в кардиологический центр, между размером дотаций фермерам и объемом производства сельхозпродукции и т. п.).

В среде Matlab необходимо построить и обучить нейронную сеть для аппроксимации таблично заданной функции, i=1, 20. Разработать программу, которая реализует нейросетевой алгоритм аппроксимации и выводит результаты аппроксимации в виде графиков.

Аппроксимация заключается в том, что, используя имеющуюся информацию по f (x), можно рассмотреть аппроксимирующую функцию z (x) близкую в некотором смысле к f (x), позволяющую выполнить над ней соответствующие операции и получить оценку погрешности такой замены.

Под аппроксимацией обычно подразумевается описание некоторой, порой не заданной явно, зависимости или совокупности представляющих ее данных с помощью другой, обычно более простой или более единообразной зависимости. Часто данные находятся в виде отдельных узловых точек, координаты которых задаются таблицей данных. Результат аппроксимации может не проходить через узловые точки. Напротив, задача интерполяции — найти данные в окрестности узловых точек. Для этого используются подходящие функции, значения которых в узловых точках совпадают с координатами этих точек.

Задача. В среде Matlab необходимо построить и обучить нейронную сеть для аппроксимации таблично заданной функции (см. рисунок 5).

Рисунок 5. Таблица значений функции В математической среде Matlab в командном окне записываем код программы создания и обучения нейронной сети.

Для решения воспользуемся функцией newff (.) — создание «классической» многослойной НС с обучением по методу обратного распространения ошибки, т. е. изменение весов синапсов происходит с учетом функции ошибки, разница между реальными и правильными ответами нейронной сети, определяемыми на выходном слое, распространяется в обратном направлении — навстречу потоку сигналов. Сеть будет иметь два скрытых слоя. В первом слое 5 нейронов, во втором — 1. Функция активации первого слоя — 'tansig' (сигмоидная функция, возвращает выходные векторы со значениями в диапазоне от — 1 до 1), второго — 'purelin' (линейная функция активации, возвращает выходные векторы без изменений). Будет проведено 100 эпох обучения. Обучающая функция 'trainlm' - функция, тренирующая сеть (используется по умолчанию, поскольку она обеспечивает наиболее быстрое обучение, но требует много памяти).

Код программы:

P = zeros (1, 20);

for i = 1: 20%создание массива P (i) = i*0.1; %входные данные (аргумент) end T= [2.09 2.05 2.19 2.18 2.17 2.27 2.58 2.73 2.82 3.04 3.03 3.45 3.62 3.85 4.19 4.45 4.89 5.06 5.63 5.91]; %входные данные (значение функции) net = newff ([-1 2.09], [5 1],{'tansig' 'purelin'}); %создание нейронной сети net. trainParam. epochs = 100; %задание числа эпох обучения net=train (net, P, T); %обучение сети y = sim (net, P); %опрос обученной сети figure (1);

hold on;

xlabel ('P');

ylabel ('T');

plot (P, T, P, y,'o'), grid; %прорисовка графика исходных данных и функции, сформированной нейронной сетью.

Результат работы нейронной сети.

Результат обучения (см. рис.2): график показывает время обучения нейронной сети и ошибку обучения. В этом примере нейронная сеть прошла все 100 эпох постепенно обучаясь и уменьшая ошибки, дошла до 10^-2,35 (0,455 531).

Рисунок 2. Результат обучения нейронной сети График исходных данных и функции, сформированной нейронной сетью (см. рис.3): кружками обозначены исходные данные, а линия — функция, сформированная нейронной сетью. Далее по полученным точкам можно построить регрессию и получить уравнение аппроксимации (см. рисунок 8). Мы использовали кубическую регрессию, так как ее график наиболее точно проходит через полученные точки. Полученное уравнение имеет вид:

y=0.049x³+0.88x²-0.006x+2.1.

Таким образом, видим, что используя нейронную сеть, можно довольно быстро найти функцию, зная лишь координаты точек, через которые она проходит.

Рисунок 3. График исходных данных и функции, сформированной нейронной сетью

Рисунок 4. График функции аппроксимации

2.3 Анализ алгоритма обратного распространения ошибки

Алгоритм обратного распространения ошибки осуществляет так называемый градиентный спуск по поверхности ошибок. Не углубляясь, это означает следующее: в данной точке поверхности находится направление скорейшего спуска, затем делается прыжок вниз на расстояние, пропорциональное коэффициенту скорости обучения и крутизне склона, при этом учитывается инерция, то есть стремление сохранить прежнее направление движения. Можно сказать, что метод ведет себя как слепой кенгуру — каждый раз прыгает в направлении, которое кажется ему наилучшим. На самом деле шаг спуска вычисляется отдельно для всех обучающих наблюдений, взятых в случайном порядке, но в результате получается достаточно хорошая аппроксимация спуска по совокупной поверхности ошибок.

Несмотря на достаточную простоту и применимость в решении большого круга задач, алгоритм обратного распространения ошибки имеет ряд серьезных недостатков. Отдельно стоит отметить неопределенно долгий процесс обучения. В сложных задачах для обучения сети могут потребоваться дни или даже недели, а иногда она может и вообще не обучиться. Это может произойти из-за следующих нижеописанных факторов.

1. Паралич сети

В процессе обучения сети, значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут выдавать на выходе сети большие значения, где производная функции активации от них будет очень мала. Так как посылаемая обратно в процессе обучения ошибка пропорциональна этой производной, то процесс обучения может практически замереть. В теоретическом отношении эта проблема плохо изучена. Обычно этого избегают уменьшением размера шага (скорости обучения), но это увеличивает время обучения. Различные эвристики использовались для предохранения от паралича или для восстановления после него, но пока что они могут рассматриваться лишь как экспериментальные.

2. Локальные минимумы

Как говорилось вначале, алгоритм обратного распространения ошибки использует разновидность градиентного спуска, т. е. осуществляет спуск вниз по поверхности ошибки, непрерывно подстраивая веса в направлении к минимуму. Поверхность ошибки сложной сети сильно изрезана и состоит из холмов, долин, складок и оврагов в пространстве высокой размерности. Сеть может попасть в локальный минимум (неглубокую долину), когда рядом имеется более глубокий минимум. В точке локального минимума все направления ведут вверх, и сеть неспособна из него выбраться. Статистические методы обучения могут помочь избежать этой ловушки, но они медленны.

3. Размер шага

Алгоритм обратного распространения ошибки имеет доказательство своей сходимости. Это доказательство основывается на том, что коррекция весов предполагается бесконечно малой. Ясно, что это неосуществимо на практике, так как ведет к бесконечному времени обучения. Размер шага должен браться конечным, и в этом вопросе приходится опираться только на опыт. Если размер шага очень мал, то сходимость слишком медленная, если же очень велик, то может возникнуть паралич или постоянная неустойчивость.

4. Временная неустойчивость

Если сеть учится распознавать буквы, то нет смысла учить «Б», если при этом забывается «А». Процесс обучения должен быть таким, чтобы сеть обучалась на всем обучающем множестве без пропусков того, что уже выучено. В доказательстве сходимости это условие выполнено, но требуется также, чтобы сети предъявлялись все векторы обучающего множества прежде, чем выполняется коррекция весов. Необходимые изменения весов должны вычисляться на всем множестве, а это требует дополнительной памяти; после ряда таких обучающих циклов веса сойдутся к минимальной ошибке. Этот метод может оказаться бесполезным, если сеть находится в постоянно меняющейся внешней среде, так что второй раз один и тот же вектор может уже не повториться. В этом случае процесс обучения может никогда не сойтись, бесцельно блуждая или сильно осциллируя. В этом смысле алгоритм обратного распространения ошибки не похож на биологические системы.

Заключение

Нейронные сети хорошо осуществляют сглаживание или подбор значений функций по точкам. Нейронные сети могут подобрать большинство функций. Причем, это могут быт как функции одной переменной, так и нескольких.

В данной курсовой работе было представлено, каким образом нейронные сети способны помочь людям в генерации знаний, которые основывались бы на всех первоначальных данных. Исследования в области нейронных сетей в основном достаточно наглядны. По сравнению с другими вычислительными методами в статистике и науке они имеют значительные преимущества. Так, у моделей на основе нейронных сетей очень гибкие теоретические требования; кроме того, им необходимы совсем небольшие объемы предварительных знаний относительно формирования задачи.

В соответствии с задачами в курсовой работе было выполнено следующее.

1. Проведен обзор алгоритмов обучения нейронных сетей.

2. Рассмотрены методы ускорения обучения нейронной сети.

3. Изучены области применения нейронных сетей.

4. Рассмотрен алгоритм обратного распространения ошибки.

5. Реализован алгоритм обратного распространения ошибки на примере аппроксимации функции.

В ходе выполнения данной курсовой работы была построена и обучена нейронная сеть для аппроксимации таблично заданной функции, i=1,20 в среде Matlab. Разработана программа, которая реализует нейросетевой алгоритм аппроксимации и выводит результаты аппроксимации в виде графиков.

Для решения использована функция newff (.) — создание «классической» многослойной НС с обучением по методу обратного распространения ошибки.

Как мощный механизм обучения нейронные сети могут широко применяться в различных областях. Существует, однако, возможность недоразумений в оценке методик машинного обучения. Они никогда не смогут полностью заменить людей в процессе решения задачи. Нейронные сети должны использоваться для обобщения данных, а не для определения, атрибуты и критерии которого весьма важны при сборе данных. Нейронные сети адаптивны по своей природе, они могут подражать решению проблемы человеком, но они не сообщат нам, какой из критериев решения задачи должен быть принят во внимание перед сбором данных. Кроме того, обучающиеся машины часто используются при формализации знаний из данных реального мира, но сами обучающиеся машины не могут генерировать принципы формализации.

1. Бестенс Д., Ван ден Берг, Вуд Д. Нейронные сети и финансовые рынки. — М.: Диалектика, 2009. — 224 с.

2. Вороновский Г. К. Махотило К.В. Петрашев С. Н. Сергеев С.А. — Генетические алгоритмы, искусственные нейронные сети и проблемы виртуальной реальности — СПб.: БХВ-Петербург, 2007. — 544 с.

3. Горбань А. Н, Хлебопрос Р. Г. Демон Дарвина. Идея оптимальности и естественный отбор — Вильямс, 2011. — 83 с.

4. Горбань А. Н, Дунин-Барковский, Кирдин А. Н. Нейроинформатика. МЦНМО, 2010. — 143 с.

5. Заенцев И. В Нейронные сети. Основные модели. — ВГУ. 2011. — 321c.

6. Федотов В. Х. Нейронные сети в экономике Чебоксары, 2006. — 171с.

7. http://ru. wikipedia.org/wiki/Нейронная_сеть

8. http://www.statsoft.ru/HOME/TEXTBOOK/modules/stneunet.html

9. http://mechanoid. narod.ru/nns/base/index.html#golovko

10. http://www.scorcher.ru/neuro/science/neurocomp/mem52. htm

11. http://www.neuroproject.ru/neuro. php