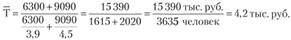Средняя арифметическая величина и ее свойства

Средняя, являясь характеристикой всей совокупности, должна ориентироваться на итоговый, так называемый определяющий, показатель, связанный со всеми единицами этой совокупности. Например, при расчете средних затрат на единицу продукции таким показателем является объем затрат на всю продукцию; при вычислении средней заработной платы определяющий показатель — это фонд заработной платы; при определении средней выработки одного рабочего таким показателем является объем продукции, произведенной всеми рабочими.

При замене индивидуальных значений признака их средней величиной определяющий показатель должен сохранять свое значение. Если при замене индивидуальных значений признака необходимо сохранить без изменения его общий объем, то применяют среднюю арифметическую; чтобы неизменной оставалась итоговая величина, обратная индивидуальным значениям признака, используют гармоническую среднюю. Если нужно, чтобы без изменений оставалась сумма квадратов исходных величин, то применяют среднюю квадратическую величину. Для сохранения неизменным произведения исходных значений признака рассчитывают среднюю геометрическую.

При расчете средней арифметической определяющий показатель можно представить алгебраически в виде суммы слагаемых: 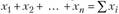. Учитывая, что определяющий показатель должен оставаться без изменения при замене всех его исходных значений их средней величиной, запишем следующее равенство:

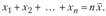
Средняя величина определяется по формуле.

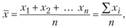
где х — индивидуальные значения признака; п — число единиц совокупности.

Приведенная формула есть формула средней арифметической простой (невзвешенной). Для расчета ее применяют в том случае, если индивидуальные значения признака не повторяются или встречаются одинаковое число раз, т. е. имеют одинаковый вес. Например, для определения среднего объема товарооборота в расчете на одну торговую организацию региона необходимо общий объем товарооборота торговых организаций региона разделить на число этих организаций.

Однако в исходных данных, особенно при использовании совокупностей большого объема, одни и те же значения признака повторяются. В этом случае данные представляются в сгруппированном виде: для каждого значения усредняемого признака сообщается частота tuо повторения, т. е. предварительно составляется ряд распределения. Допустим, варьирующим признаком является срок функционирования банка, который соответствует периоду времени, прошедшему с момента регистрации в центральном банке. Условные данные приведены в табл. 3.1.

Таблица 3.1

Продолжительность функционирования коммерческих банков

Для вычисления средней продолжительности функционирования банка по данным, приведенным в табл. 3.1, можно использовать простую среднюю арифметическую. Следовательно, средняя величина составит 10 лет (70: 7).

По этим же данным предварительно можно составить ряд, показывающий распределение банков по продолжительности периода деятельности, а затем определить величину средней (табл. 3.2). В совокупностях, в которых одни и те же значения признака многократно повторяются, проводят группировку данных, объем совокупности определяют не путем суммирования отдельных значений признака, а путем перемножения (взвешивания) его вариантов на число единиц, соответствующих каждому варианту, т. е. на их частоты: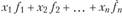

Поскольку должно выполняться равенство.

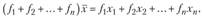
средняя определяется по формуле средней взвешенной.

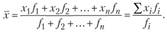
Таблица 3.2

Группировка коммерческих банков по продолжительности периода деятельности

Согласно этой формуле в нашем примере (см. табл. 3.2) средний срок деятельности банков составит.

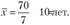
В отдельных случаях веса могут быть представлены в виде относительных величин структуры (в процентах или долях единицы). Тогда формула средней арифметической взвешенной будет иметь вид.

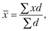
где 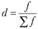- доля каждой группы в общем числе единиц совокупности (частость).

Если частоты выражены в долях (коэффициентах), то 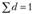и формула средней арифметической упрощается: /.

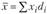Так, в приведенном выше примере количество банков с разным сроком службы соответственно составляет 14,3% (0,143); 57,1% (0,571); 28,6% (0,286) их общего числа. Средний срок деятельности банка составит.

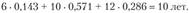
В тех случаях когда исходная информация представлена в виде интервального ряда распределения, в качестве вариантов усредняемого признака (х) принимают середины интервалов, вычисляемые по каждой группе, как полусуммы нижних и верхних границ интервалов. Рассмотрим условный пример (табл. 3.3).

Вычислим значение среднего объема активов:

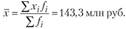
Средняя арифметическая обладает рядом свойств, которые могут быть использованы для упрощения ее вычисления и других целей.

Таблица 3.3

Распределение кредитных организаций по объему активов

В статистическом анализе применяют следующие основные свойства средней арифметической.

1. Сумма отклонений отдельных значений признака от средней арифметической равна нулю:

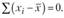
2. Сумма квадратов отклонений значений признака от средней меньше суммы квадратов отклонений от любой произвольной величины А:

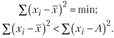
3. Если от каждого значения признака отнять или к каждому его значению прибавить одно какое-либо число А, то новая средняя соответственно уменьшится или увеличится на то же самое число:

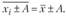
4. Произведение средней на сумму частот всегда равно сумме произведений вариантов на частоты:

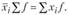
5. Если каждое значение признака разделить или умножить на одно какое-либо число А, то новая средняя соответственно уменьшится или увеличится во столько же раз:

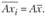
6. Если значения признака веса разделить или умножить на одно и то же число, то величина средней не изменится:

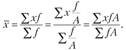
С помощью средних обобщают не только абсолютные, но и относительные величины. Отличия в расчетах в этом случае отражают особенности построения средних, которое может быть выполнено на основе значений как первичных, так и вторичных признаков.

Порядок расчета и форма средней зависят от взаимосвязи изучаемых признаков и от того, какими данными мы располагаем.

Средние первичных признаков определяются по формуле простой средней путем деления итогового подсчета по характеризуемому признаку на перечневый подсчет, т. е. числитель такого отношения представляет собой общую сумму значений усредняемого признака у всех единиц совокупности, а знаменатель — общее число единиц изучаемой совокупности.

Базой для расчета средних значений вторичного признака является исходное соотношение первичных признаков, определяющих логическую формулу усредняемого вторичного признака. Далее вычисляется частное от деления итоговых подсчетов по этим первичным признакам. В случае когда один из итоговых показателей неизвестен, расчет средней производят на основе исходных данных о значении усредняемого вторичного признака каждой отдельной единицы совокупности и связанного с ним признака — веса. Таким образом, средняя вторичного признака имеет вид средней взвешенной.

Если известны значения знаменателя исходного соотношения, но не известны значения числителя, то среднюю вычисляют по формуле средней арифметической. В противном случае среднюю рассчитывают по формуле средней гармонической. Для каждого показателя, используемого в экономическом анализе, можно составить только одно исходное соотношение для расчета средней (ИСС).

Если, например, требуется рассчитать средний размер вклада в банке, то исходное соотношение будет следующим:

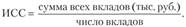
Если же необходимо определить среднюю ставку процента по кредитам, выданным на один и тот же срок, то потребуется следующее исходное соотношение:

Для расчета средней заработной платы работников предприятия необходимо общий фонд заработной платы разделить на число работников:

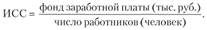
Числитель исходного соотношения средней отражает ее определяющий показатель. Рассмотрим пример на основе данных о работе двух организаций (табл. 3.4).

Таблица 3.4

Данные о работе организаций

Требуется определить средние значения всех представленных в таблице признаков.

В этом примере единица совокупности — одно предприятие, поэтому среди представленных в таблице признаков первичными являются плановый и фактический объемы выпускаемой продукции. Следовательно, для расчета средней величины каждого из этих признаков нужно применить формулу простой средней: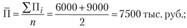

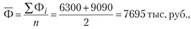
где - число предприятий.

Следующий признак в таблице — процент выполнения плана, который представляет собой относительную величину, рассчитанную по формуле.

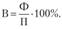
Среднее значение процента выполнения плана по совокупности предприятий можно представить в виде отношения обобщенных значений тех же признаков, каждое из которых охватывает всю изучаемую совокупность единиц:

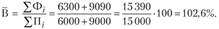
Поскольку единицей совокупности, как уже отмечалось, в нашем примере является одно предприятие, выработка одного рабочего — это вторичный признак. Отсюда для расчета ее среднего значения нужно применить формулу взвешенной средней. Исходными для такого расчета будет следующее соотношение:

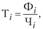
где 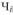- численность рабочих предприятия.

В соответствии с рассмотренной выше методикой определения средней величины вторичного признака можно записать:

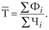
Для определения средней выработки одного рабочего необходимо предварительно вычислить численность рабочих, занятых на каждом предприятии. В соответствии с исходными данными это можно сделать по формуле.

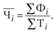
Проведя необходимую подстановку, получаем следующее выражение искомой средней, которое соответствует формуле средней гармонической взвешенной:

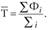
Подставив в формулу числовые значения, находим.