Метод цепной лестницы

Идея метода цепной лестницы (Chain Ladder Method) (метода пошагового восхождения) заключается в том, чтобы выяснить, как увеличивалась сумма оплаченных убытков в прошлом от одного отчетного периода к другому и принять, что зга же схема сохранится и в будущем^[1]. Этот метод предполагает, что при отсутствии экстремальных факторов (инфляции, изменений в составе портфеля, изменений законодательства и др.) распределение интервалов между моментами наступления страхового случая и его урегулирования относительно устойчиво во времени. Поэтому, за исключением случайных колебаний, столбцы в треугольнике убытков оказываются пропорциональными:

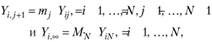(4.7).

где 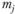- случайная величина, отражающая изменение (инфляцию) платежей в промежутке между периодами оплаты с номерам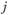и и 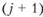; 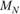- случайная величина, отражающая изменение платежей в промежутке между периодами с номерами N до окончательного урегулирования убытков, т. е. обозначает инфляцию стоимости страховых случаев, произошедших в данный финансовый период, по прошествии N финансовых периодов.

Величины 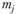и 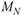называют коэффициентами развития. Предполагается, что их значения не зависят от периода i.

Метод цепной лестницы реализуется по следующему алгоритму.

Этап 1. Оценка коэффициентов развития.

Коэффициент развития показывает, во сколько раз в среднем совокупная сумма убытков, оплаченных в последующем периоде развития, больше соответствующего значения в предыдущем периоде:

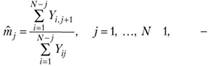(4.8).

где 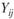- совокупный (накопленный) размер платежей в финансовом периоде с номером j (квартале, году) по страховым случаям, происшедшим в период с номером i (4.5); N — число периодов, представленных в треугольнике развития.

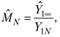(4.9).

где 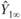- окончательный совокупный (накопленный) размер платежей (или его оценка) по всем страховым случаям, наступившим в первом периоде (предполагается известным); 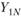- совокупный (накопленный) размер платежей в N-м (последнем треугольника развития) финансовом периоде по страховым случаям, произошедшим в первом периоде.

Для оценки резервов 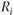необходимо подсчитать шаг за шагом оценки коэффициентов 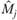, которые отражают изменение выплат после периода с номером j.

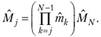(4.10).

Этап 2. Расчет значений будущих выплат по формуле.

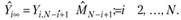(4.11).

Этап 3. Оценка резерва убытков к концу каждого i-го периода по формуле.

(4.12).

Этап 4. Находим оценку общего РПНУ по формуле (4.6).

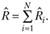
Кроме явных достоинств метода цепной лестницы, таких как простота, доступность и очевидность, у него имеются некоторые недостатки, а именно:

• • оценка треугольника развития может быть затруднена, когда для различных периодов развития используются разные наборы данных;
• • метод очень чувствителен к изменениям даже одного числа, т. е. он неустойчив;
• • метод является статистически неубедительным, поскольку при расчете берут произведение математических ожиданий не являющихся независимыми случайных величин;
• • метод не учитывает искажение треугольника развития под воздействием внешних факторов;
• • в методе не учитывается информация о заработанной страховой премии.

И все же метод используется большинством страховых компаний и включен во все основные актуарные учебники. Для устранения указанных недостатков в настоящее время актуариями разработано множество различных модификаций метода цепной лестницы.

ПРИМЕР 4.4^[2]

Имеются данные о выплатах страховой компании — треугольник развития совокупных (накопленных, кумулятивных) платежей за четыре года (табл. 4.11). Согласно оценке, общая стоимость страховых случаев, наступивших в первом году, достигнет 178 у.е. Требуется рассчитать страховые резервы произошедших, но нс заявленных убытков методом цепной лестницы (пошагового восхождения).

Таблица 4.11

Треугольник выбывания (развития) совокупных платежей Y_ij в у.е. к концу финансового года с номером j по страховым случаям, произошедшим в году с номером i.

Решение

Этап 1. Используя алгоритм метода цепной лестницы (пошагового восхождения), найдем значения коэффициентов развития по формуле (4.8):

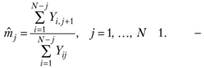
У нас

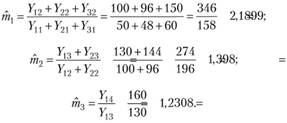
По условию задачи 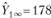у.е., поэтому по формуле (4.9) получаем следующую оценку размера инфляции последнего 4-го года:

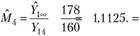
Далее необходимо подсчитать шаг за шагом (в обратном порядке, от предпоследнего года к первому) оценки коэффициентов которые отражают изменение выплат после года с номером j по формуле (4.10):

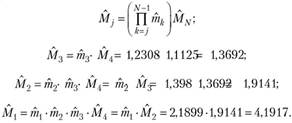
Этап 2. Рассчитаем оценки совокупной стоимости всех платежей по страховым случаям (будущие выплаты) по формуле (4.11):

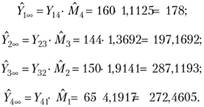
Для наглядности сведем наши расчеты в матрицу, представляющую совокупные убытки нарастающим итогом.

Оценки будущих выплат рассчитаем по формуле (4.7):

Например,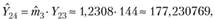

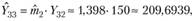
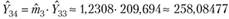и т. д.

Выделенный в таблице серым цветом нижний треугольник матрицы представляет собой оценку развития выплат методом цепной лестницы:

ъ
				177,231.	197,169.
			209,694.	258,085.	287,119.
		142,3417.	198,988.	244,908.	272,46.

Этап 3. Теперь можем вычислить размер резерва по каждому году по формуле (4.12):

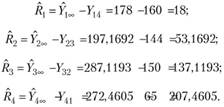
Этап 4. Оценка общего РИНУ составит по (4.6):

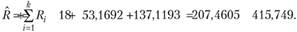
Ответ: общий размер РПНУ равен 415,749 у.е.

• [1] Мак Т. Указ, соч.; Лемер Ж. Указ. соч.
• [2] Прообраз задачи см.: Лемер Ж. Указ. соч.