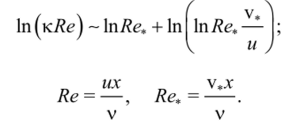Турбулентный пограничный слой
Характерная скорость v. турбулентных пульсаций, вообще говоря, меняется с расстоянием х. Поэтому толщина h пограничного слоя также должна зависеть от х. Для того чтобы определить эту зависимость, оценим производную dh/dx. Для этого учтем, что при у = h скорость турбулентного течения направлена примерно вдоль поверхности пограничного слоя — это и определяет положение граничной поверхности… Читать ещё >
Турбулентный пограничный слой (реферат, курсовая, диплом, контрольная)
При выводе формулы (108) мы рассматривали течение вдоль бесконечной пластины. При обтекании же реальных тел с конечными размерами логарифмический профиль скорости реализуется лишь на относительно небольшом расстоянии от тела, называемом турбулентным пограничным слоем. Вне этого слоя течение ламинарно и, как и в случае вязкого пограничного слоя, может рассматриваться как идеальное.
Пусть вдоль полубссконсчной пластины течет поток со скоростью и (рис. 18). Оценим закон изменения толщины турбулентного пограничного слоя вблизи этой пластины.
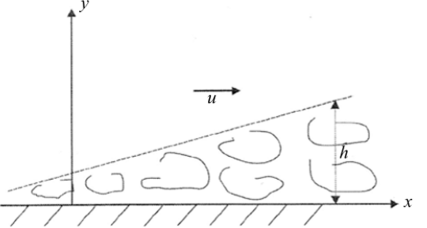
Рис. 18.
На границе турбулентного пограничного слоя средняя скорость турбулентного потока непрерывно переходит в скорость и. Обозначив h толщину пограничного слоя и учитывая уравнение (108), имеем.
Характерная скорость v. турбулентных пульсаций, вообще говоря, меняется с расстоянием х. Поэтому толщина h пограничного слоя также должна зависеть от х. Для того чтобы определить эту зависимость, оценим производную dh/dx. Для этого учтем, что при у = h скорость турбулентного течения направлена примерно вдоль поверхности пограничного слоя — это и определяет положение граничной поверхности. Следовательно, на этой границе производная dhldx должна быть равна тангенсу наклона скорости турбулентного течения. На поверхности пограничного слоя горизонтальная составляющая скорости турбулентного потока по порядку величины должна быть равна скорости и основного потока. Вертикальная же компонента должна быть равна скорости V, пульсаций. Действительно, другой величины, имеющей размерность скорости, для определения вертикальной компоненты скорости в нашем распоряжении сейчас нет. Поэтому по порядку величины dh / dx ~ v. / и, следовательно, h ~ v"x / и. Используя это соотношение в уравнении (108), получаем.
Уравнение (ПО) неявно определяет зависимость v, отх и, следовательно, функцию /?(х). Получим теперь явную приближенную оценку этой зависимости. Для этого перепишем (ПО) в следующем виде:
При турбулентных течениях Re, Re, «1, значит, логарифмы от этих чисел Рейнольдса также велики. Поскольку большое число намного больше своего логарифма, вторым членом в правой части последнего соотношения можно пренебречь. Следовательно, в первом приближении 1п/?е, ~ 1п (к, Кс?). Используя это приближение для оценки логарифма в правой части (110), получаем.
Отсюда.
Поскольку логарифм — медленно меняющаяся функция, v, слабо зависит от х. Возвращаясь к соотношению h ~ v, x / и, приходим к выводу, что толщина турбулентного пограничного слоя почти линейно (чуть медленнее) возрастает с х. Интересно напомнить, что толщина пограничного слоя при ламинарном течении изменяется по закону h ~ х½.