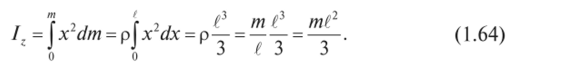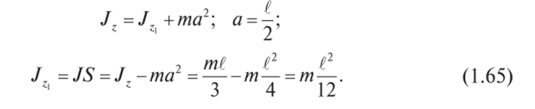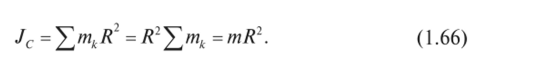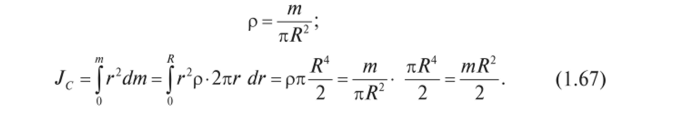Момент инерции тела относительно оси

Моментом инерции тела (системы) относительно данной оси O_z (или осевым моментом инерции) называется скалярная величина, равная сумме произведений масс всех точек тела (системы) на квадрат расстояния до этой оси.

Момент инерции тела относительно любой оси является величиной положительной и не равной нулю.

Осевой момент инерции играет при вращательном движении тела такую же роль, какую масса при поступательном движении, т. е. осевой момент инерции является мерой инертности тела при вращательном движении.

Для одной материальной точки, находящейся на расстоянии И от оси, J. =mh².

Единицы измерения J. в системе СИ 11 кг • м²]. Определим моменты инерции некоторых однородных тел, форму которых имеют большинство звеньев механизмов:

1. Тонкий однородный стержень длиной / и массой т.

Вычислим момент инерции относительно оси О., перпендикулярной оси стержня и проходящей через его конец (см. рис. 1.77). Для любого элементарного отрезка длиной dx h = x, а масса dm = pdx, где р = у — масса единицы длины стержня. Переходя от суммы к интегралу, получим:

Для определения момента инерции относительно центральной оси, т. е. оси, проходящей через центр тяжести S (см. рис. 1.78), воспользуемся теоремой Гюйгенса.

Рис. 1.78.

Момент инерции тела относительно любой оси равен моменту инерции относительно оси, ей параллельной и проходящей через центр тяжести тела, плюс произведение массы всего тела на квадрат расстояния между осями.

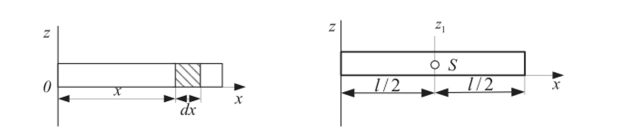
Рис. 1.77.

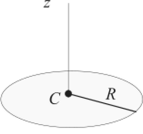
2. Тонкое круглое кольцо радиусом R и массой т (рис. 1.79). Поскольку все частицы кольца находятся на расстоянии R от оси Cz, то.

3. Круглый диск или цилиндр радиусом R и массой т (рис. 1.80).

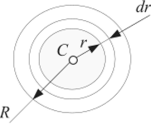
Рис. 1.79 Рис. 1.80.

Выделим элементарное кольцо радиусом г и шириной dr. Площадь кольца 2лrdr.

Масса единицы площади диска: