Математическая модель теплообмена в ленточно-поточном канале

В настоящее время в практике мирового производства пластинчатых теплообменников применяются пластины с горизонтальными и наклонными гофрами. Пластины первого типа образуют ленточно-поточные каналы с двухмерным движением теплоно;

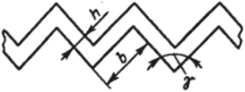
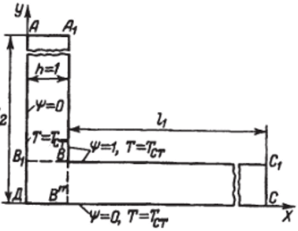
Рис. 7.4. Геометрические характеристики канала ленточно-поточного типа сителей, а пластины второго типа — щелевидные каналы сетчато-поточного типа с ярко выраженным трехмерным движением теплоносителей. Основной особенностью течения теплоносителей в каналах обоих типов является многократное периодически повторяющееся изменение направления движения потока, которое может иметь как ламинарный, так и турбулентный характер.

Рассмотрим канал ленточно-поточного типа, образованный пластинами с горизонтальными гофрами с углом при их вершине у = 90°; продольное сечение канала представлено на рис. 7.4. Процесс стационарного конвективного теплообмена при ламинарном течении жидкости в таком канале описывается системой дифференциальных уравнений в частных производных, включающих уравнения Навье — Стокса, неразрывности и энергии. Допустим, что физические свойства жидкости не зависят от температуры (о = const, а = const, р = const). Тогда для вынужденного двухмерного движения потока несжимаемой жидкости эта система уравнений имеет вид:

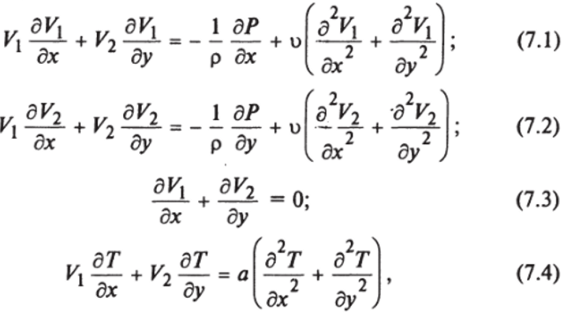
где а — коэффициент температуропроводности (а = Х/ср); х, у — координаты; V, Vi — скорости жидкости по координатам х и у, м/с; и — коэффициент кинематической вязкости (о = ц/р), м/с.

Чтобы исключить параметр давления (Р), выполним операцию дифференцирования уравнения (7.1) по у, а уравнения (7.2) — по х и, вычтя из первого второе, а также введя понятие завихренности о.

получим.

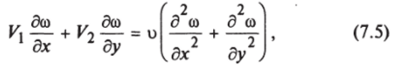
или в векторной форме.

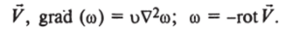
Теперь, введя функцию тока (у) и.

и подставив (7.7) и (7.8) в уравнения (7.4), (7.5) и (7.6), получим.

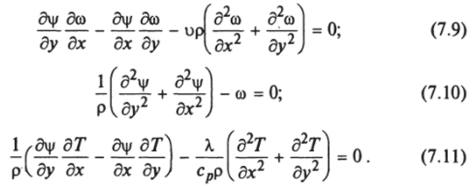
Для первых двух слагаемых уравнений (7.9) и (7.11) справедливы соотношения:

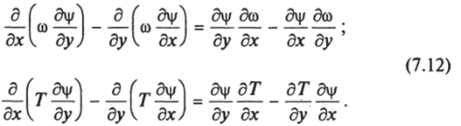
Используя (7.12), приведем уравнения систем (7.9), (7.10) и (7.11) к единому каноническому виду.

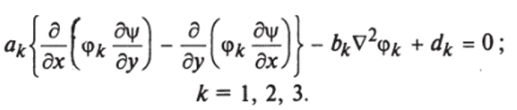
Здесь <�р* соответствует конкретным неизвестным системы — а), ф, Г, а коэффициенты д*, ?*, с/* выбираются из приведенных ниже данных:

Система уравнений (7.9) и (7.11) решалась для одного поворота щелевидного канала (см. рис. 7.4) со следующими граничными условиями:

1) на стенке приняты условия «прилипания», т. е. У = V₂ = = 0, и, соответственно, функция тока имеет вид:

Ф_с = const.

Для завихренности со на стенке использовалось приближенное конечно-разностное граничное условие Вудса.

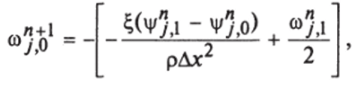
где j = 0 соответствует линия сетки, совпадающая со стенкой;

2) температура стенки канала принималась постоянной.

что примерно соответствует случаю нагрева теплоносителя конденсирующимся паром;

3) прямолинейные участки каналов АВ и ВС (см. рис. 7.4) выбирались достаточно длинными, чтобы можно было считать течение в сечениях АА и СС установившимся. В расчетах 1 и 1₂ принимались соответственно равными (3−5)А и (5−9)h в зависимости от числа Re. Это позволило принять в сечениях АА и CCj параболический профиль скорости и граничное условие для ф и со:

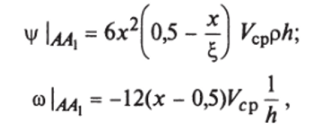
где? — коэффициент гидравлического сопротивления канала; Кр — средняя скорость жидкости в канале; х = ijh — относительное расстояние от стенки канала.

Аналогично записываются граничные условия для сечения СС,;

• 4) профиль температуры во входном сечении принят согласно решению Л. Эрнста и Х. Ханемана для установившегося течения в плоском канале с постоянной температурой стенки;
• 5) в выходном сечении использовались два вида граничных условий для температуры:
  • а) регулярный тепловой режим

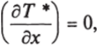
ТТ

где 7* = - - -; Гс, Гц — температура стенки, жидкости в центральной части ^/с" ^/ц канала соответственно;

б) полный прогрев жидкости.

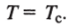
Вычисления показали, что решение незначительно зависит от вида граничных условий для Т на выходе.

В результате расчетов на ЭВМ было получено распределение в ленточном канале функции тока у, завихренности о, скоростей К[ и Кг, температуры Т при числах Рейнольдса от 60 до 800. Для больших Re вычисления не производились в связи с возрастанием времени счета, а также с некорректностью допущения установившегося течения на выходе из канала в этом случае. Число Прандтля принималось равным 1, т. е. о = а.

Картина течения жидкости в изогнутом канале на основе распределения линий тока показана на рис. 7.5 и 7.6. Из рисунков видно существенное различие в характере движения жидкости, к основным особенностям которого следует отнести наличие отрыва потока, зон возвратных течений, зон оттеснения потока (на участке А’В перед углом Л и на участке В «С напротив угла В) и зон присоединения потока после зон возвратных течений (на участках ВС' и ДВ'). Такой характер определяет наличие составляющей скорости потока, перпендикулярной стенке канала и, соответственно, возникновение конвективной составляющей переноса тепла в поперечном направлении при теплообмене в ламинарном потоке.

Картину течения жидкости в канале с изгибом дополняет анализ распределения скоростей потока, определяемых по формулам (7.7) и (7.8). Типичные эпюры скоростей в различных сечениях каналов для Re = 300 представлены на рис. 7.7.

Их анализ показывает существенное перераспределение профиля скорости в канале в районе поворота потока. На различ;

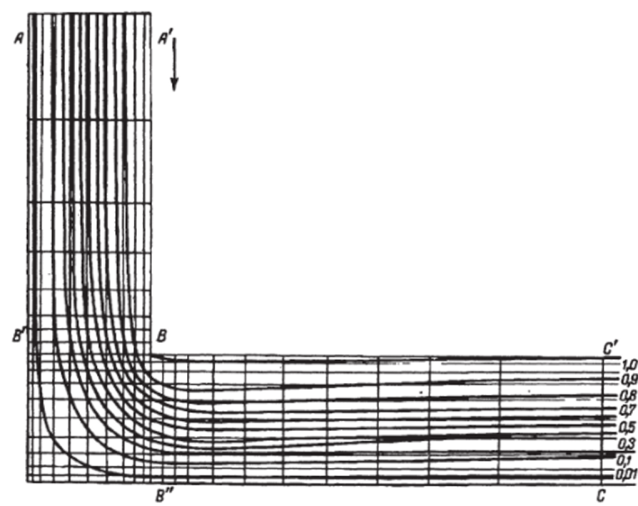
Рис. 7.5. Распределение линий тока в канале при Re = 100.

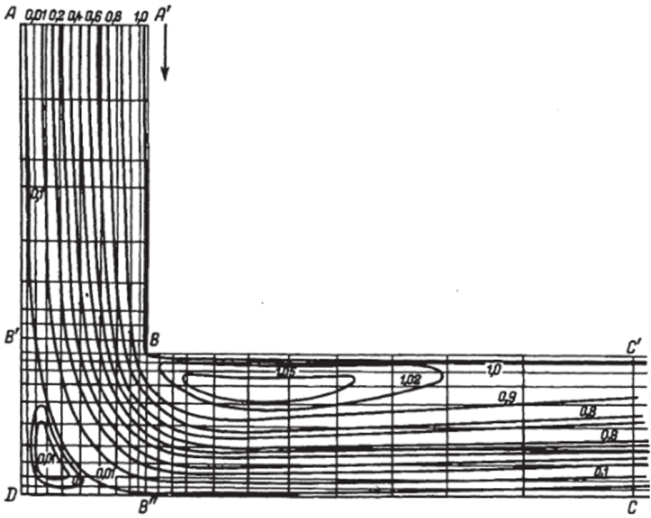
Puc. 7.6. Распределение линий тока в канале при Re = 800.

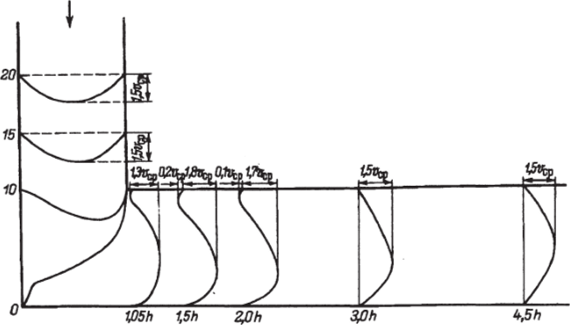
Рис. 7.7. Эпюры скоростей в различных сечениях канала (Re = 300).

ных участках канала наблюдаются следующие зоны: ускорения потока в областях оттеснения и удара (по стенкам А’В и ДС, рис. 7.6), замедления скорости потока в районе рециркуляции и изменения знака скоростей, зоны выравнивания профиля скоростей и приближения его к профилю течения Пуазейля в плоском канале с прямолинейными стенками вдали от поворота.