Вихревые движения идеальной баротропной жидкости. 
Теорема томсона и ее следствия

Рассмотрим совокупность материальных точек (элементарную частицу), занимающих в момент времени t шар малого радиуса с центром в точке, радиус-вектор которой равен г. Если через dr обозначить вектор из центра шара к какой-либо его точке, то поле скоростей в элементарной частице равно.

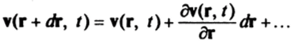
Членами второго порядка малости относительно dr пренебрежем, а оператор dv/dr представим в виде.

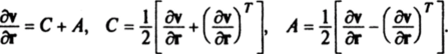
Оператор С симметричен, а оператор А кососимметричен и соответствует операции векторного умножения: Adr э со х dr, со = = ½ rot v. Симметрический оператор С определяет поле скоростей деформаций элементарной частицы, а оператор А — ее вращение как твердого тела. Поле скоростей точек элементарной частицы представляется суммой переносной скорости центра элементарной частицы, поля скоростей деформаций и поля скоростей вращения элементарной частицы как твердого тела, т. е. v (r + dr, t) a v (r, /) + + Cdr + to x dr.

0.4.1. Вектор О = rot v называется вихрем скорости.

Рассмотрим «жидкую» материальную линию L, состоящую из одних и тех же материальных точек. Для материальной линии справедлива параметризация (рис. 65).

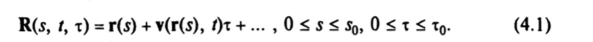
Вычислим интеррал.

где a (i, t) — единичный вектор, касательный к линии L, a s — натуральный параметр.

0.4.2. Интеграл (4.2) называется циркуляцией скорости вдоль кривой L.

Если L — замкнутый контур, то Г[Д) — циркуляция вдоль контура L.

Л. (Томсон). Производная по времени циркуляции скорости вдоль материальной жидкой линии вычисляется по формуле

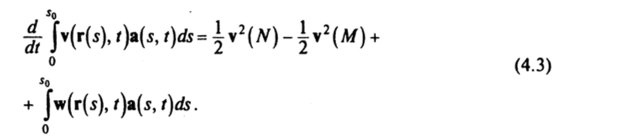
? Производная по времени в (4.3) равна.

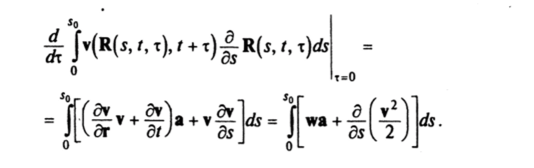
Отсюда и следует равенство (4.3), если учесть выражение для ускорения (1.2). ?

С. 1. Если жидкий материальный контур L замкнут, то точка М совпадает с точкой N и

С. 2. Если на замкнутый контур L натянуть гладкую поверхность Е, то по формуле Стокса

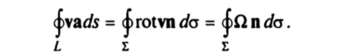
Здесь п — нормаль к поверхности I, из конца которой обход контура L происходит против часовой стрелки. Согласно равенству (4.4).

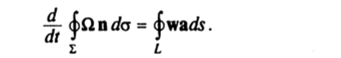
Т (Томсон). Если массовые силы потенциальны, а идеальная жидкость баротропна, то циркуляция по любому жидкому материальному контуру остается постоянной во все время движения.

А Уравнение Эйлера (2.3), описывающее движение жидкости в этом случае, имеет вид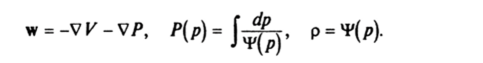

Далее.

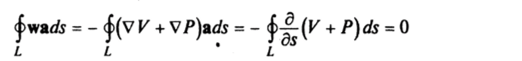
и согласно формуле (4.4) циркуляция скорости по замкнутому контуру L постоянна. ?

С. (Лагранж). Если в начальный момент времени поле скоростей идеальной баротропной жидкости, движущейся в потенциальном поле, было безвихревым (rot v = 0), то вихрь скорости будет равен нулю во все время движения.

А По теореме Томсона и следствию 2.

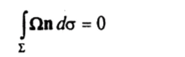
во все время движения для любой гладкой поверхности Е, поскольку вихрь скорости П = 0 в начальный момент времени. Учитывая произвольность поверхности I, приходим к выводу, что О = 0 в рассматриваемой области движения во все моменты времени. ?

Теорема Томсона и ее следствие позволяют выделить важный класс потенциальных течений идеальной баротропной жидкости, когда поле скоростей v (r, /) ищется в виде Vtp (r, t), где <�р (г, /) — скалярное поле — потенциал скоростей. Особенно эффективным оказывается этот подход при исследовании плоских движений идеальной несжимаемой жидкости, так как в этом случае применим аппарат теории функций комплексного переменного и конформных отображений.