Эксергия теплоты. 
Техническая термодинамика и теплопередача

При термодинамическом анализе теплоэнергетических установок во многих случаях приходится оценивать работоспособность той теплоты, которая преобразуется в работу в циклах. Максимальное количество полезной работы, которое можно получить в цикле при заданных температурах источников теплоты, называется работоспособностью (эксергией) теплоты.

Максимальную работу, как известно, можно получить в тепловом двигателе, работающем по циклу Карно. Термический КПД такого цикла записывается в виде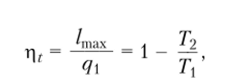

где q — количество теплоты, подведенной к рабочему телу; 1 и Т₂ — температуры высшего и низшего источников теплоты; /_шах = q_{ — q₂ — максимальное количество работы, которое можно получить в обратимом цикле.

Выражая /_тах из последней формулы, получаем.

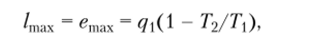
где (1 — Т₂/Т) — коэффициент качества теплоты (эксергетической ценности теплоты). Последнюю формулу можно записать в виде.

Величина e_max представляет собой максимальную работу, которую можно получить в некотором идеальном обратимом цикле. Из формулы (2.15) следует, что для получения полезной работы используется лишь часть некоторого количества теплоты q. Другая ее часть, равная величине q = r₂(<7i/ri), отдается НИТ (рассеивается в окружающей среде).

Таким образом, работа, получаемая при использовании теплоты q> не может превысить величину e_max даже в идеальном обратимом цикле. В реальном же процессе добавляются еще потери, возникающие вследствие его необратимости, равные T₂As_Heo^_p. В результате действительная работа в реальном процессе всегда меньше e_max, т. е.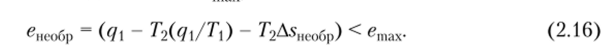

Часть теплоты q_{, не превращающаяся в работу, равная ~T₂(qJT) — — Г₂А5_необр, была названа анергией. Анергия — это потеря эксергии, равная произведению температуры НИТ на сумму приращений энтропии всех тел, участвующих в процессе.

Из первого закона термодинамики следует, что сумма эксергии и анергии в любом процессе остается постоянной. Согласно второму закону термодинамики, эксергия остается постоянной лишь в обратимых процессах. В необратимых процессах она уменьшается, превращаясь в анергию. Если энергия бесполезно рассеивается в окружающей среде, то вся эксергия превращается в анергию.

Как следует и, а формул (2.15) и (2.16), эксергия зависит от температур ВИТ (энергоносителя) и НИТ (окружающей среды).

Например, 1 Дж теплоты, отдаваемой горячим воздухом с температурой 473 К при температуре окружающей среды 293 К, будет более работоспособен, чем 1 Дж теплоты, отдаваемой этим же воздухом при температуре, допустим, 373 К при той же температуре среды. Таким образом, чем больше отличаются параметры НИТ и ВИТ, тем выше работоспособность. В случае если температуры энергоносителя и среды одинаковы, то эксергия равна нулю.

Чтобы подсчитать эксергию единицы теплоты, следует в формулах (2.15) и (2.16) взять <7, = 1 Дж. Тогда эксергия 1 Дж, например, при Т = АТд К и Т₂ = 293 К будет.

Как и следовало ожидать, во втором случае эксергия оказалась меньше.

Эксергия будет тем больше, чем менее необратим процесс. Тем больше в этом случае будет получено полезной работы. Все это позволяет ввести понятие так называемой эксергетической эффективности процесса, или эксергетического КПД. Оп определяется отношением использованной эксергии к подведенной. Например, для теплообменников это будет отношение эксергии теплоносителя на выходе е" 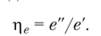к его эксергии на входе е'

Эксергетический КПД позволяет учесть потери только из-за необратимости процессов, так как лишь в необратимых процессах происходит потеря эксергии. Поэтому для анализа всех обратимых циклов (теоретически обратимые циклы, цикл Карно) он неприменим — во всех этих случаях ц_е = 1. Тем не менее, эксергетический метод анализа необратимых тепловых процессов получил в последнее время широкое распространение. Особое значение он приобрел при оценке эффективности технологических процессов.

Обычно тепловые потери выявляют путем составления теплового баланса установок, т. е. исследуют статьи расхода теплоты. Однако такой баланс дает лишь количественную картину распределения потерь. Более того, он искажает действительную картину потерь теплоты и особенно в тех случаях, когда, например, пар поступает не на технологические нужды, а для совершения работы. В таких случаях наиболее целесообразно составлять эксергетический баланс.

11а основе эксергетического метода анализа, например, подсчитано [3], что из 64,5% потерь работоспособности теплоты (эксергии) в паротурбинной установке 53,6% приходится на долю котла, а на долю конденсатора — всего 2,2%. Отсюда ясно, что низкотемпературная теплота дает ничтожную часть потери работоспособности. Тогда как энергетический баланс «отдает» на потери в конденсаторе почти половину теплоты, получаемой от сжигания топлива. На потери в котле он дает лишь 16% теплоты, однако именно здесь, где температура энергоносителя максимально отличается от температуры окружающей среды, происходит наибольшая (53,6%) потеря работоспособности. Кроме того, баланс на основе составления расходов эксергии дает возможность учесть аэродинамические потери в турбине, вообще не учитываемые в тепловом балансе, но имеющие значительную величину (7%).

Таким образом, эксергетический баланс, дополняя тепловой, позволяет понять качественную картину распределения потерь теплоты и наметить пути их устранения.

Расчеты на основе эксергетического метода анализа позволяют избежать ошибок принципиального характера. Так, при подсчете энергетического КПД некоторых тепловых установок получают величины, превышающие 100%. Такой КПД получается, например, для кондиционеров, работающих с использованием эффекта Пельтье (если пропускать электрический ток через два спаянных полупроводника, то в месте спая тепло будет выделяться, а на свободных концах поглощаться или, наоборот, в зависимости от направления тока).

Проведем анализ энергетических превращений, наблюдающихся в этом случае, с учетом эксергии |7|. Допустим, чтобы поддерживать в помещении температуру 20 °C (293 К), при наружной температуре 5 °C (278 К), температура теплых спаев кондиционера должна быть около 40 °C (313 К). В этом случае кондиционер отдает на обогрев помещения 360 Вт, а затрачивает электроэнергии только 200 Вт, т. е. 160 Вт теплоты отбирается из окружающей среды. Если подсчитать энергетический КПД, то он оказывается равным 180% - (360: 200) • 100% = 180%. Такой результат может привести к ошибочному мнению, что энергию, находящуюся в окружающей среде, можно концентрировать без каких-либо затрат и тем самым получить неисчерпаемый ее источник. Однако это противоречит второму закону термодинамики. Тогда какова же причина столь высокого энергетического КПД?

Чтобы ответить на этот вопрос, применим эксергетический метод анализа. Найдем эксергию 360 Вт теплоты, отдаваемой в помещении,.

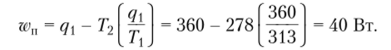
Таким образом, работоспособность теплоты здесь всего 40 Вт. Эксергетический КПД в данном случае будет равен.

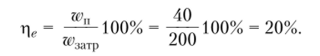
Так как электроэнергия работоспособна на 100% (стопроцентная эксергия), то затраченная эксергия взята равной подведенному количеству электроэнергии (а'здтр = 200 Вт).

40 Вт — это то количество электроэнергии, которое нужно было бы затратить на обогрев помещения, если бы КПД кондиционера был равен 100%. Из 360 Вт тепла, затраченных на обогрев, 320 Вт обесценились в самой установке. Из них 160 Вт подведенной электроэнергии, а еще 160 Вт было взято холодными спаями кондиционера из окружающей среды.

Если бы эксергетический КПД кондиционера мог быть равным 100%, то электроэнергии на обогрев затрачивалось бы 40 Вт, а 320 Вт можно было бы взять из окружающей среды. Однако эти 320 Вт неработоспособны, с их помощью нельзя произвести никакой работы и, таким образом, о концентрировании энергии нс может быть и речи. 11роето энергия, затраченная на обогрев (200 Вт), была «разбавлена» в кондиционере 160 Вт энергии, взятой из окружающей среды, которая неработоспособна.

В этом примере энергия как бы появлялась без каких-либо затрат. Можно привести обратный пример [7], когда она как бы исчезает, если опять-таки не учитывать, что работает не энергия вообще, а лишь эксергия.

Допустим, для нагрева 100 л воды с 25 °C (293 К) до 30 °C (303 К) требуется 12 561 кДж теплоты. 11одечитаем, на какую высоту можно поднять 75 кг груза, используя эту теплоту. Килоджоули переведем в килограммометры:

12 561 • 101,98= 1 281 000.

Разделив полученный результат на 75, получим высоту поднятия груза. Она будет равна 17 км.

Однако подсчитаем работоспособность 12 561 кДж теплоты.

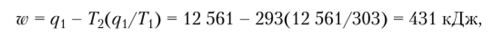
т.е. из 12 561 кДж при такой небольшой разнице температур работоспособны лишь 431 кДж. Высота поднятия груза в этом случае составит только 0,5 км.

Эти два примера показывают, к каким неверным оценкам может привести неучет качества энергии. Только определив эксергию, можно правильно оценивать полезность энергоресурсов и принять верное решение об их рациональном использовании.

Таким образом, эксергетический метод анализа позволяет исключить многие неверные оценки и связанный с ними ущерб для экономики.