Анализ точности однофакторного уравнения регрессии

При анализе точности однофакторной регрессионной модели решаются задачи, связанные с построением доверительных интервалов для коэффициентов регрессии ?>, доверительной области линии истинной регрессии и доверительной области прогнозов наблюдений отклика У (х) при заданных значениях факторов X = х.

Рассмотрим оценку точности линейной модели регрессии.

Доверительные интервалы для коэффициентов регрессии.

Доверительные интервалы для параметров b_Q и Ь{ при надежности оценки 1 — а равны:

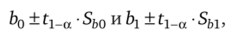
где П__а — квантиль t-распределения (Стьюдента) с числом степеней свободы п — 2; Ь₀, Ь_г — оценки коэффициентов регрессии, полученные при решении нормальных уравнений (10.2); S_b0, S_bl — оценки стандартных отклонений коэффициентов регрессии.

Для S_b0, S_bl выполняются следующие свойства:

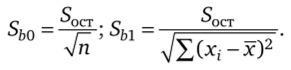
Число связей (коэффициентов) для линейной модели I = 2, поэтому остаточная дисперсия.

При вычислении Sm удобно пользоваться результатом, полученным Бартлетом: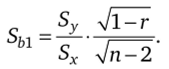

Пример 10.1.

Результаты однофакторного регрессионного анализа для линейной модели зависимости поверхностной плотности трикотажа от суммарной длины нити в петлях (в сквозной задаче) показаны в табл. 10.1.

Для свободного члена b₀ (Intercept) и коэффициента наклона Ь_г (Slope) приведены их оценки, стандартные ошибки S_b0 и S_M, отношения Стьюдента 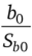и 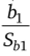для проверки гипотезы Н₀: Ь'_ь = Ъ? = 0 и их вычисленные уровни значимости.

Таблица 10.1

Таблица однофакторного регрессионного анализа.

Малые уровни значимости говорят о том, что коэффициенты линейной регрессии ДхД = 672,34 — 39,75xj являются значимыми (значимо отличаются от нуля).

Доверительные области линии истинной регрессии и прогнозов наблюдений отклика. Построим область, ограниченную доверительными границами для средних значений отклика у (х). Доверительные пределы отклика для средней точки С (х, у) равны границам параметра Ь₀, обозначим их через y_min и у_тах (рис. 10.2). Граничные значения коэффициента наклона обозначим через bimin и hmaxЧерез каждую из точек (x;y_min) и (х; у_тах) проводятся две прямые с коэффициентами наклона b_lmin и b_lmax. Искомая область представляет собой максимальную область, охватываемую этими прямыми, она называется также доверительной трубкой. В этой области линия регрессии лежит с вероятностью (1 — а)², равной произведению надежности оценки (1 — а) для каждого параметра Ъ₀ и Ь_х. В точке х = х границы доверительной области наиболее близки друг другу. Расположение границ показывает, что прогнозы по уравнению регрессии будут справедливыми только в случае, если значения х, не выходят за пределы выборки, по которой вычисляется уравнение регрессии. Отсюда следует, что экстраполяция по уравнению регрессии может привести к значительным погрешностям.

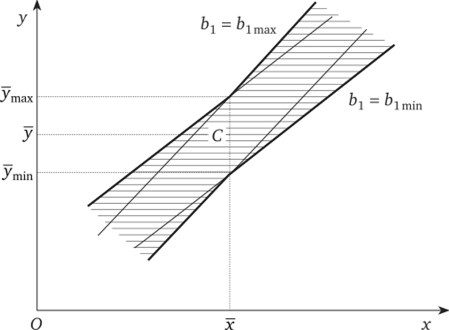
Рис. 10.2. Доверительная область линии истинной регрессии.

Доверительная область линии истинной регрессии для поверхностной плотности трикотажа показана на рис. 10.3.

На графике также показаны доверительные границы для прогноза значений наблюдений у — пунктирными линиями, более удаленными от линии регрессии.

В некоторых случаях выборка, состоящая из точек (х" у,), содержит грубые ошибки, выбросы. Происхождение их может быть самым различным: сбой в работе измерительной аппаратуры, ошибка при переписывании выборочных значений, попадание в данные наблюдений из другого опыта и т. п.

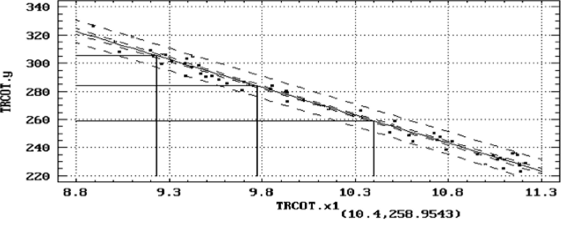
Рис. 10.3. Доверительные области для линейной регрессии поверхностной плотности трикотажа у по фактору х, (скриншот Statgraphics).

Присутствие ошибочных наблюдений в исходных данных нарушает предпосылки нормальной регрессионной модели и сказывается на результатах расчетов по методу наименьших квадратов. Для исследования влияния выбросов на статистические выводы их надо исключить из обработки, т. е. осуществить цензурирование исходных данных.

Если при исключении грубого наблюдения возрастает величина коэффициента корреляции и снижается значение остаточной дисперсии, то скорректированная линейная модель более полно представляет исходные данные.

При анализе однофакторной нелинейной регрессии у —Дх), где Дх) — параболическая или какая-либо другая нелинейная функция, содержащая два члена или более, коэффициенты регрессии вычисляются по методу наименьших квадратов (см. подпараграф 10.2.1). Доверительные интервалы для коэффициентов регрессии, доверительная область линии истинной регрессии и доверительная область линии прогноза значений у (х) оцениваются по аналогии с линейной однофакторной моделью регрессии.