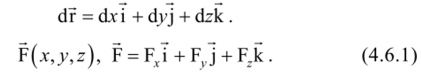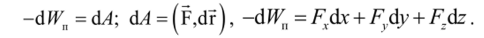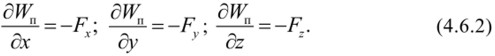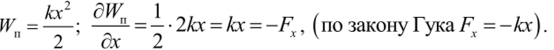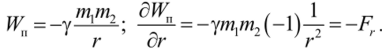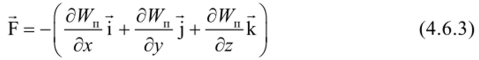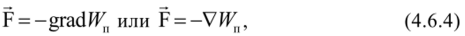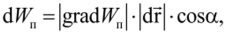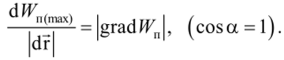Связь между потенциальной энергией и силой

Градиент потенциальной энергии

В общем случае потенциальная энергия является функцией многих координат системы материальных точек (частиц), взаимодействующих между собой. Но мы представим (получая гот же вывод), что все частицы, кроме одной, не изменяют своего положения и действие всех мы заменяем их силовым полем. Тогда потенциальная энергия частицы, движущейся среди других, lV_n(x, y, Z).

Пусть положение частицы задается радиусом-вектором в системе координат x, y, z. Введем обозначения и запишем выражения для перемещения частицы и силы, которая на нес действует:

• • перемещение
• • консервативная сила

Согласно (4.4.2) и (4.3.4), получим: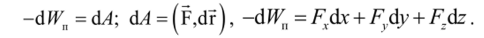

Используя полученное, последовательно определяем производную от W_a по одной из координат, считая две других постоянными (то есть выражаем частную производную).

Эти равенства согласуются с примерами, которые мы рассматривали в разделе 4.5.

Согласно 4.5.1, можно получить для взаимодействия в поле упругих сил:

Используя 4.5.3, запишем для гравитационного взаимодействия.

Подставив (4.6.2) в выражение для силы (4.6.1), получим.

Написанное в правой части последнего равенства выражение соответствует применению операции grad к потенциальной энергии Ж_п. Значит.

где V — оператор набла.

Согласно (4.6.2) направление силы F указывает направление убывания потенциальной энергии. Из равенства (4.6.4) следует что вектор — градиент направлен против силы поля, т. с. в направлении максимального возрастания потенциальной энергии.

Выясним физический смысл grad любой функции. Используя.

(4.6.4), запишем -dfV_n =(F, drj = ([-gradH^/_I1], dr), или dЖ_п =(grad (F_n, dr).

Преобразуя скалярное произведение векторов, получим.

где a — угол между вектором grad Ж и вектором dr .

Отсюда dlV_n-dJV_n{nm), при, а = grad Ж ^л dr = 0, т. е. когда drT’lF.

Предполагая, что перемещение происходит в направлении максимального возрастания потенциальной энергии, получим:

(Замечание: производная от скаляра по вектору есть вектор).

Полученное позволяет определить физический смысл введенной характеристики gradPF.

gradfF — вектор, равный пространственной скорости возрастания потенциальной энергии в направлении ее максимального возрастания.

Данная формулировка справедлива для любой величины, когда эта величина пространственно изменяется от точки к точке.

Сравнив (4.6.3) и (4.6.4), запишем, например, что.

То сеть проекции вектора gradfT на координатные оси равны производным от Ж_п по соответствующим координатам.