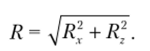Давление жидкости на криволинейные поверхности

Рассмотрим некоторую криволинейную твердую бесконечно тонкую поверхность со, находящуюся на некоторой глубине покоящейся жидкости (рис. 2.16). Координатные плоскости расположены, как показано на рисунке. Плоскость ХОУ лежит в пределах свободной поверхности жидкости. Ось 02 направлена вниз. На поверхности со действуют две силы К и /?' равные между собой и направленные навстречу друг другу.

Рис. 2.16. К определению результирующей силы давления на криволинейную поверхность.

Любую из этих сил можно разложить на три составляющие. Например, для силы К' это Я'_х, Щ_г Я'_г (см. рис. 2.16, а). Тогда искомая сила.

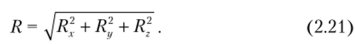
Определим сначала силу Я₂. Для этого через контур поверхности со вертикально вверх проведем цилиндрическую поверхность до пересечения со свободной поверхность жидкости (рис. 2.17).

Для того чтобы выделенный жидкий цилиндр находился в равновесии, должны выполняться следующие условия:

Е^, = 0; ЕД, = 0; Е^ = 0.

Но так как сила Я₂ входит только в третье уравнение, рассмотрим это уравнение: ЕТ_г = 0.

Из поверхностных сил будем рассматривать силы избыточного давления, т. е. исключим из рассмотрения р_л. Получаем.

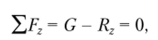
где С — вес жидкости в объеме цилиндра, ограниченного свободной поверхностью жидкости и криволинейной поверхностью со.

42_Глава 2. Гидростатика_.

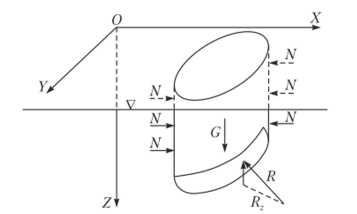
Рис. 2.17. К определению вертикальной составляющей силы давления Отсюда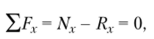

где 1К — объем цилиндра.

В результате получим, что вертикальная составляющая давления жидкости на криволинейную поверхность равн весу жидкости в объеме вертикального цилиндра, нижни основанием которого является сама криволинейная поверхность, а верхним основанием — свободная поверхност жидкости. Выделенный объем жидкого цилиндра называю телом давления (VI' =В _д).

Определим горизонтальные составляющие силы И, т. е. Я_л и /?_(/. Для определения Я_х выполним построение горизонтального цилиндра, ограниченного с одной стороны поверхностью со, а с другой стороны — координатной плоскость Юг (рис. 2.18).

Аналогично предыдущим рассуждениям силы ?), С в проекции на ось ОХ обращаются в ноль. В рассмотрени остается уравнение Х/' ⁼ 0:

где М_х — сила давления на поверхность, образованную пересечением координатной плоскости УОХ и цилиндрической поверхности.

Обозначим площадь этой плоской поверхности со' и обратим внимание на то, что со' является проекцией криволинейной поверхности на вертикальную плоскость, параллельную плоскости УОХ. Тогда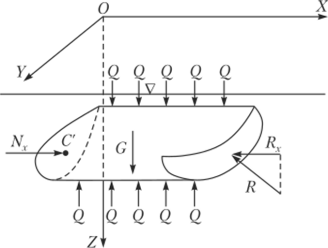

Рис. 2.18. К определению горизонтальной составляющей силы давления.

где И'_с — глубина погружения центра тяжести площади со' под уровень свободной поверхности жидкости.

В результате, так как Я_х = Ы_х, получим.

Так как составляющая Я_у горизонтальна, аналогичные рассуждения приводят к равенству.

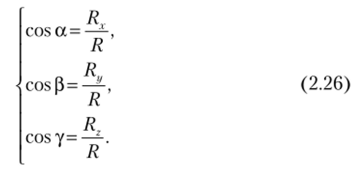I.

где со" — площадь проекции криволинейной поверхности на вертикальную плоскость, параллельную координатной плоскости ХОХ И с — глубина погружения центра тяжести со" В под уровень свободной поверхности жидкости.

Таким образом, три составляющие для определения результирующей силы давления жидкости на криволинейную поверхность будут Я_х = рф'_сьу, Я_у = рфс": Я₂ = р?1Т_|Д.

Сила Я находится по формуле (2.21), а направление силы определяется по углам а, р, у между силой и соответствующей проекцией силы (см. рис. 2.16, а):

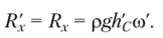
Рассмотрим два примера определения силы давления жидкости на цилиндрические поверхности.

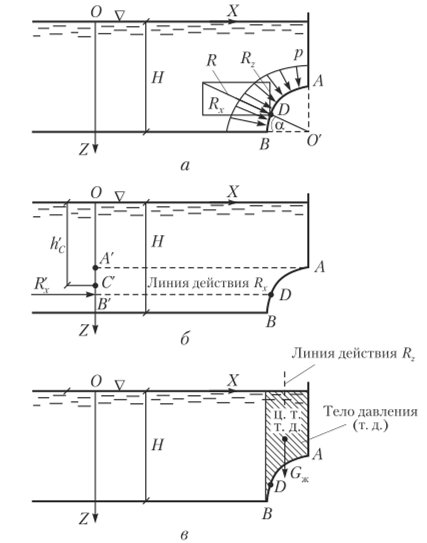
1. Жидкость действует на выпуклую цилиндрическу стенку АВ кругового очертания (рис. 2.19). Эпюра давления, результирующая сила давления Я и ее составляющи Я_х и Я₂ показаны на рис. 2.19, а. Третья составляющая отсутствует, так как поверхность АВ перпендикулярна координатной плоскости ХОУ, ее длина в этом направлении равна /.

Горизонтальная составляющая силы давления на поверхность ЛВ определяется как сила давления Я'_х на плоскую проекцию А’В' поверхности АВ на вертикальную плоскость (рис. 2.19, б)

Вертикальная составляющая Я₂ равна весу жидкости в объеме тела давления 1Т_{Г Д} (С_ж) и показана на рис. 2.19, в:

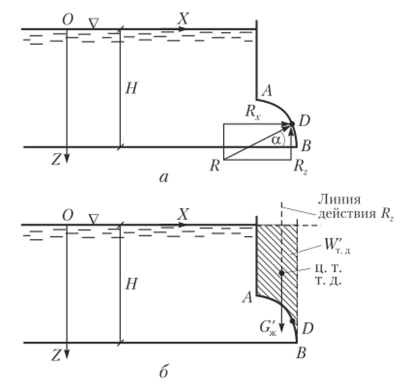
где У._ГД = со, _д/.

Рис. 2.19. Схемы действия результирующей силы (а) и ее горизонтальной (б) и вертикальной (в) проекци на цилиндрическую поверхность В рассматриваемом случае телом давления является жидкое тело, ограниченное вертикальной призмой, восстановленной по контуру цилиндрической поверхности.

Сила Л, проходит по линии действия силы тяжести (веса).

Тогда

а угол наклона силы Л определится из соотношения для угла а:

2. Жидкость действует на вогнутую цилиндрическую поверхность АВ кругового очертания (рис. 2.20).

Результирующая сила давления Л на поверхности АВ и ее составляющие Л_х и Л₂ показаны на рис. 2.20, а. Значение Л_х определяется аналогично предыдущему случа и равно Л_с = рф'₍<�о.

Вертикальная составляющая определяется как вес жидкости в объеме тела давления. Но в данном случае, если восстановить вертикальную призму через контур цилиндрической поверхности до пересечения с продолжением свободной поверхности жидкости (рис. 2.19, б), в теле призмы жидкост нет. Для того чтобы определить Л_г, мы как бы (фиктивно).

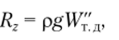
Рис. 2.20. Схема действия результирующей силы на вогнутую со стороны жидкости поверхность помещаем в тело давления жидкость. Сила И₂ будет направлена в сторону, противоположную направлению оси ОZ. Такой прием используется каждый раз, когда определяется вертикальная составляющая давления жидкости, находящейся снизу от криволинейной поверхности:

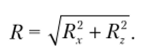
где — объем фиктивного тела давления.

Результирующая сила давления Я определится по формуле (2.28):