Оптимизация периодичности контроля в системах предоставления информационных услуг

Эффективность предоставления информационных услуг во многом определяется надежностью, информационной и функциональной безопасностью компьютерных систем и сетей, достигаемых при реализации комплекса программно-аппаратных средств оперативного и тестового контроля, которые направлены на обнаружение п минимизацию последствий деструктивных воздействий как злонамеренного, так н случайного характера.

Для компьютерных систем с целью повышения готовности к безопасному выполнению запросов и минимизации опасных состояний нарушения защищенности, существенно снижающих рентабельность предоставления информационных услуг, возникает потребность оптимизации интервалов тестирования для обнаружения нарушений защищенности в результате дестру к г и в и ы х воздейств и й.

Для систем предоставления информационных услуг, подверженных деструктивным воздействиям, оптимизация контроля, на основе известных условий функционирования защищенных информационных систем, в связи с тем, что интенсивность злонамеренных воздействий (в отличие от отказов), как правило, характеризуется неопределенностью и изменяемостью во времени. Эта особенность обусловливает потребность модификации марковской модели контроля и постановки задачи оптимизации интервалов тестирования, с целью учета неопределенности и изменяемости интенсивностей деструктивных воздействий. При решении поставленной задачи предлагается свести векторную задачу максимизации готовности системы и минимизации вероятностей ее простоев и опасных состояний к скалярной задаче оптимизации на основе критерия максимизации прибыли от информационных услуг (обслуживания запросов), позволяющего интегрировать указанные частные критерии. Разрабатываемая модель должна позволить оценить эффективность контроля с адаптацией периодичности тестирования к изменениям интенсивности вредоносных воздействий с учетом разрешения технического противоречия, связанного с достижением максимума готовности системы к безопасному предоставлению информационных услуг, минимума ее простоев, связанных с тестированием и восстановлением защищенности, а также минимума вероятности опасных состояний, необнаруженных нарушений защищенности.

Модель контроля защищенности. При построении марковской модели исследуемой системы выделим состояния: готовности системы к безопасному выполнению запросов (0); тестирования в отсутствии нарушений защищенности (1); восстановления безопасности (2); необнаруженных нарушений защищенности (3); тестирования при наличии нарушений (4) [6|. Состояние необнаруженных нарушений защищенности является опасным. В предположении идеальности тестового контроля по обнаружению всех нарушений защиты граф состояний и переходов системы приведен на рис. 11.13, по которому составляется система уравнений Колмогорова — Чепмена с использованием средств системы компьютерной математики находим вероятности всех состояний:

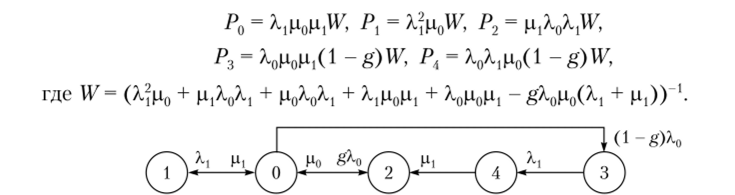
Рис. 11.13. Граф состояний и переходов системы с тестовым контролем:

л" — интенсивность деструктивных воздействий; л, — интенсивность инициализации тестового контроля; g — доля обнаруживаемых оперативным контролем нарушений защищенности; р, — интенсивность тестирования (величина, обратная среднему времени тестирования), р₀ — интенсивность восстановления безопасного состояния (величина, обратная среднему времени восстановления защиты) Оптимизация интервалов контроля защищенности. Модели контроля защищенности систем от злонамеренных деструктивных воздействий должны учитывать неопределенность интенсивностей злонамеренных воздействий и их изменений во времени. При оптимизации интервалов тестирования будем предполагать заданными векторы вариантов возможных интенсивностей деструктивных воздействий (q_t) и вероятностей этих вариантов (г_;).

Оптимизация интервалов тестирования связана с техническим противоречием достижения максимума готовности системы и минимума вероятности ее опасных состояний. Формально решение этой задачи векторной оптимизации возможно по аддитивному или мультипликативному скалярному критерию, однако такое решение сопряжено с субъективизмом назначения весов приоритета частных критериев.

Избежать субъективности векторной оптимизации позволяет формирование объективного критерия, имеющего некоторый физический смысл и интегрирующего частные критерии. В качестве такого критерия предлагается критерий «прибыль от обслуживания запросов». Будем считать, что каждый запрос, поступающий в состоянии готовности системы к его безопасному выполнению, обеспечивает прибыль s₀. Запрос, поступающий в состоянии простоя, дает меньшую прибыль s, (s, < л₀), что обусловлено дополнительными задержками по завершению тестирования и (или) восстановления системы после обнаружения ее нарушений. Запрос, поступающий в опасном состоянии необнаруженных нарушений защищенности, приводит к убыткам (штрафу) — s₃.

Таким образом, математическое ожидание прибыли от обслуживания запроса вычисляется как.

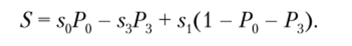
При неопределенности потока деструктивных воздействий рассмотрим варианты В1—ВЗ оптимизации интервалов тестирования, обеспечивающих максимум прибыли при обслуживании запросов.

При варианте В1 определяется значение интервала тестирования 1/Л., обеспечивающее максимум прибыли при обслуживании запросов, по критерию.

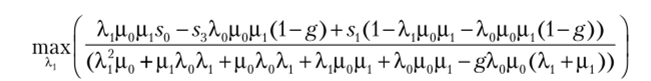
и- 1.

при средней интенсивности воздействий Х₀ =? q, r,.

i=0.

При варианте В2 с учетом всех возможных интенсивностей воздействий q_t (i = 0, 1,…, п — 1) определяется оптимальный, усредненный по всем интенсивностям воздействий, интервал тестирования 1Д₍, обеспечивающий максимум прибыли обслуживания запросов, по критерию.

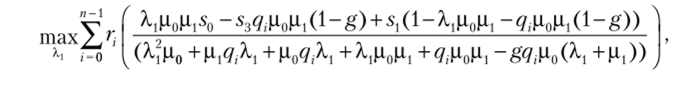
где q_t — i-й вариант возможной интенсивности деструктивных воздействий, вероятность которого г_г

При варианте ВЗ для возможных интенсивностей деструктивных воздействий, задаваемых вектором (г/,), определяется вектор оптимальных интенсивностей инициализации тестирования (я,), обеспечивающих максимум прибыли обслуживания запросов, по критерию.

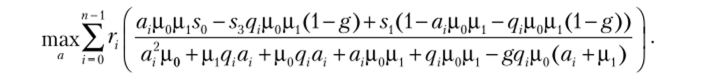
Адаптация интервалов тестирования в процессе функционирования требует периодических измерений (мониторинга) интенсивностей деструктивных воздействий с определением градаций интенсивности q_t и соответствующих интервалов тестированием (предварительно установленных при оптимизации или рассчитываемых в реальном времени). Следует заметить, что адаптация интервалов тестирования может вызвать замедление вычислительного процесса, а поэтому требует сравнения выигрыша и затрат на ее реализацию.

Пример оптимизации. Приведем пример оптимизации интервалов тестирования системы по критерию максимизации прибыли. Будем считать, что заданы ц, = 1 1/ч, р₀ = 0,1 1 /ч, g = 0,6, s₀= 1 у.е., 5,= 0,1 у.е., s₂= 100 у.е., варианты интенсивностей деструктивных воздействий и их вероятности, представленные векторами: q = (0,001; 0,002; 0,003; 0,004; 0,005; 0,006) и г = = (0,1; 0,15; 0,3; 0,2; 0,15; 0,1). Для вариантов В1 и В2 оптимальным интервалам тестирования, обеспечивающим максимум прибыли S при обслуживании каждого запроса, соответствуют = 0,5824 1/ч и А., = 0,5802 1/ч. Для варианта ВЗ вектор оптимальных интенсивностей инициализации тестирования (я,), обеспечивающий максимум прибыли 5 при обслуживании каждого запроса, равен а = (0,020; 0,028; 6,035; 0,040; 0,045; 0,049).

Результаты расчета математического ожидания максимально возможной прибыли от выполнения запроса с адаптацией периодичности контроля к изменениям интенсивности деструктивных воздействий и без нее представлены на рис 11.14. Кривая 1 соответствует варианту ВЗ адаптивного изменения периодов контроля в зависимости от наблюдаемой интенсивности деструктивных воздействий. Кривая 2 соответствует вариантам Bl, В2,.

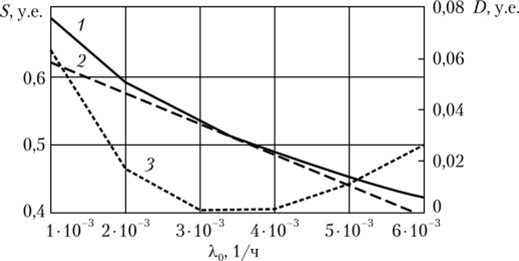
Рис. 11.14. Зависимость максимальной прибыли обслуживания запросов от интенсивности деструктивных воздействий при которых задается постоянный период тестирования, вне зависимости от реальной интенсивности деструктивных воздействий. Кривая 3 отражает разницу прибыли от обслуживания запросов с адаптацией периода контроля к изменениям интенсивности деструктивных воздействий и без нее. Представленные графики показывают эффективность адаптации периодов тестирования защищенности к изменениям интенсивности деструктивных воздействий.

Таким образом, мы показали эффективность адаптивного задания периодов тестирования с целью максимизации прибыли при предоставлении информационных услуг в зависимости от измеряемой интенсивности деструктивных воздействий.