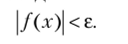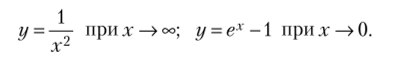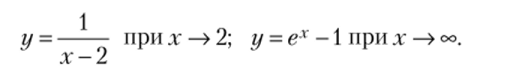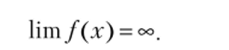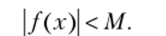Величины бесконечно малые, бесконечно большие и ограниченные

Начнем с того, что выделим несколько важных классов переменных величин.

Определение 6.3. Функция y = f (x) называется бесконечно малой в данном процессе, если она имеет предел равный нулю: lim/(х) = 0. (Если не указано, как изменяется х, принципиально возможен процесс любого типа.).

Поскольку в этом случае b равно нулю, то неравенство f (х)-Ь определяющее предел, для бесконечно малой приобретает следующий вид:

Разумеется, в конкретных 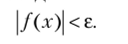задачах необходимо указывать процесс изменения аргумента, например функция у = (х-1)²— бесконечно малая при х, стремящимся к единице; в других случаях она таковой не является.

Следует иметь в виду, что наименование бесконечно малая не выражает размера величины (это не одна тысячная и даже не одна миллионная), а отражает лишь характер ее изменения как переменной в данном процессе.

Пример 6.1.

Определение 6.4. Переменная величина называется бесконечно большойу если в процессе изменения ее модуль становится (и остается таковым) больше любого сколь угодно большого положительного числа М: |/(лг)|>М.

Пример 6.2.

Переменная величина, обратная бесконечно малой, является бесконечно большой, а переменная величина, обратная бесконечно большой, является бесконечно малой. Бесконечно большие величины не имеют предела. Это выражают записью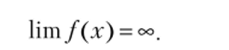

Определение 6.5. Функция называется ограниченной в данном процессе, если начиная с некоторого момента ее значения (по модулю) остаются меньше некоторого положительного числа М («момент» характеризуется числами N и 8 соответственно в процессах 1-го и 2-го типов):

Все функции, имеющие предел, и в частности бесконечно малые, являются ограниченными, между тем как бесконечно большие — неограниченные.

Пример 6.3.

Функция y = sinx — ограничена в любом процессе; напротив, например, z/ = xsinx при ж—— неограниченная величина, но не бесконечно большая.