Пространственные особенности городских систем

Городские системы выполняют экономические и неэкономические функции.

Экономическими являются промышленные, транспортные, торгово-распределительные и снабженческие функции. К неэкономическим относятся административно-политические, культурные, научные, организационные функции. С точки зрения функциональной нагрузки городских поселений, выделяют градообразующие и градообслуживающие функции, каждая из которых может включать как экономические, так и неэкономические функции.

Градообразующей называют деятельность по обслуживанию экономических, культурных, административных, научных и других связей.

Деятельность по удовлетворению потребностей самого города (в том числе промышленных и транспортных) называют градообслуживающей.

В зависимости от объема и характера выполняемых функций, городские системы делятся на монои полифункциональные. Монофункциональные городские системы — преимущественно небольшие поселения курортного, научного, промышленного профиля, а также районные центры. В отдельных случаях понятие монофункциональной городской системы может рассматриваться как аналог моногорода. Однако стоит отметить, что, по сравнению с отдельным моногородом, монофункциональная городская система характеризуется большей экономической и социальной устойчивостью, благодаря наличию сложных многоуровневых системных связей с функциональными элементами окружающей территории.

Примерами полифункциональных городских систем являются, кроме Москвы и Санкт-Петербурга, межрегиональные (Самара, Екатеринбург, Новосибирск), республиканские и областные центры, а также центры федеральных округов. Существует прямая зависимость между количеством и масштабами функций города и численностью его населения. Как правило, нолифункциональные города отличаются большей людностью и более быстрым ростом населения. Функциональная структура города влияет на половозрастной и профессиональный состав населения, образовательный уровень и образ жизни. В городах с преобладанием металлургической, химической, горнодобывающей промышленности среди населения высока доля мужчин; в текстильных центрах, наоборот, преобладают женщины.

Кроме функциональной дифференциации, города, как саморазвивающиеся системы, различаются еще по типу и структуре. В них постоянно меняется динамика структурно-территориальных зон: изменяются территориальные пропорции в направлении центр — периферия, а также функциональная нагрузка на отдельные здания или районы. Иными словами происходит перенос на новые территории социопространственных континуумов (например, промышленных, управленческих и административно-хозяйственных объектов, зон рекреации). Поэтому городским системам свойственна определенная иерархическая организация, пространственная неравномерность, взаимодействие и динамичность [2,3].

Стремление выявить и описать иерархию населенных мест строгими логическими или математическими моделями возникло в XIX веке. На материалах изучения расселения и сетей обслуживания Южной Германии, немецкий ученый Вальтер Кристаллер в 1933 году разработал теорию центральных мест. Исходя из идеализированного допущения об односторонности территории, равномерности размещения на ней ресурсов, одинаковой плотности и покупательной способности населения, а также равномерности транспортной инфраструктуры, Кристаллер предположил, что территориальное расположение населенных пунктов имеет определенные закономерности. Пример системы расселения Кристаллера приведен на рисунке 6. Приведенная на рисунке система охватывает территорию трёх сопредельных государств: Германии, Австрии и Швейцарии [33−35].

В системе Кристаллера главный город размещается в центре и окружён соподчиненными ему населёнными пунктами, располагающимися в углах шестиугольной решетки. Каждый такой шестигранник с семью населенными пунктами входит в более обширную зону, насчитывающую до 49 пунктов (7×7), притом главный город центрального шестигранника является центральным для всей зоны [33−35]. Все города — элементы системы Кристаллера, имеют чётко выраженную иерархическую структуру, взаимосвязаны между собой многообразными хозяйственно-экономическими отношениями и имеют чётко разграничивающиеся зоны влияния (рис. 6). Модель Кристаллера относится к идеальным моделям размещения городов, то есть моделям, нацеленным на поиск оптимального размещения географических объектов в однородном пространстве: на равнине с одинаковой плотностью и покупательной способностью населения, одинаковыми транспортным сообщением и другими параметрами.

В теории Кристаллера — город — центр для всех других населенных пунктов данного района, обеспечивающий их товарами и услугами. Центральное место обслужива;

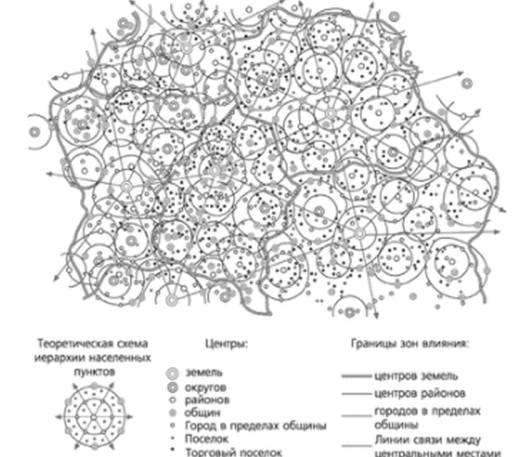
Рис. 6. Модель системы расселения Кристаллера.

ет дополняющие районы. Эта теория нашла широкое применение в географии и других областях знаний с 50-х гг. XX в. Последующие попытки создать теоретические модели, адекватно описывающие реальное распределение населенных мест и центров обслуживания в регионах и городах, в основном исходили из идеи Кристаллера. Например, американский географ Уолтер Изард, один из основателей региональной науки, модифицировал и усложнил эту схему, исходя из влияния городских агломераций. Схематическое представление модели систем расселения по Изарду приведено на рисунке 7 [4].

Сравнивая схемы Кристаллера и Изарда (рис. 6, 7), на первый взгляд может казаться, что модель Изарда похожа на модель Кристаллера. Однако в схеме Изарда нашла отражение структурно-функциональная организация городской агломерации. Её принципиальными отличиями являются более упорядоченные связи между центрами городских агломераций и соподчиненными им территориями. Добавим, что в модели Изарда более развиты периферийные связи в пределах крупных агломераций. Наличие этих связей снижает функциональную значимость центров агломераций, повышая автономность отдельных их элементов.

Одним из способов изучения иерархии населенных мест является анализ соотношений между рангом и размером городов. Подобная закономерность была найдена социологом Джоржем Зипфом (в русской транскрипции — Ципфом), по имени которого она называется правилом Ципфа «ранг-размер». Согласно правилу Ципфа в простейшем случае население любого города стремится быть равным числу жителей самого крупного города, деленного на его порядковый номер (ранг) в системе городов страны:

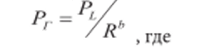
P_f — население рассматриваемого города;

P_L — население самого крупного города;

№ — ранг данного города; b — коэффициент, зависящий от условий рассматриваемого города.

Правило Ципфа выведено эмпирически и часто отвечает не совокупности всех городов страны, а лишь ее части. Позднее высказывались предположения, что закон Ципфа описывает распределение систем расселения. Правило Ципфа и его модификации анализировались многими исследователями применительно к разным территориям и историческим периодам [4J.

Важной особенностью современных городских систем является их пространственная неравномерность. Она обусловлена неоднородностью городских систем, испытывающих воздействие центростремительных процессов на сосредоточение различных видов хозяйственной деятельности. Другими факторами, обусловливающими пространственную неравномерность городов, являются географические особенности территории, цены на землю, взаимное расположение зон промышленности и жилой застройки, транспортная инфраструктура.

Математическое моделирование широко используется для изучения особенностей городских систем и основной целью имеет выявление количественных показателей расселения. Наиболее известна модель американского исследователя Колина Кларка, описывающая пространственную неравномерность распределения плотности населения в городе. Она является выражением эмпирически установленной зависимости внутригородского расселения от удаленности района по отношению к центру. Приняв в качестве основной, наиболее универсальной характеристики внутригородского расселения, плотность населения, Кларк показал, что эта величина уменьшается экспоненциально с увеличением расстояния от центра города:

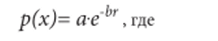
р (х) — средняя плотность населения в городе;

Рис. 7. Схема модели расселения по Иларду [4].

а — плотность населения в центральных кварталах города;

г — расстояние до центра города; b — коэффициент пропорциональности, свойственный каждому городу.

В литературе оценке этой модели уделено большое внимание. Отмечено, однако, что неоднородность условий в городе, особенно транспортных, приводит к отклонениям от модели Кларка, особенно в части распределения плотности населения. Если же в качестве меры расстояния использовать не геометрическое расстояние до центра, а время его достижения, то модель будет лучше соответствовать начальному распределению плотности населения с учетом сосредоточенности расселения вдоль радиальных магистралей.

На основе анализа территориально-пространственной структуры городов и ее сопоставления с ценами на земельные участки в городах США были разработаны дифференцированные графические модели структуры города: концентрическая (Е. Барджес), секторная (X. Хойт), многоядерная Ч. Гарриса и Е. Ульмана, показанные на рисунке 8 [2, 4, 36].

Модели интерпретируют территориальную структуру города и выделяют городские районы разного уровня: деловые, жилые, промышленные. Пространственно-территориальное размещение отдельных районов в городах является результатом взаимодействия комплекса социально-экономических, природно-географических, историко-архитектурных и других факторов. Их расположение определяется функциональной нагрузкой, значимостью для городской среды, связью с другими районами и транспортной доступностью. Например, жилые районы должны располагаться с учётом удобного доступа к местам трудовой деятельности. В свою очередь, на качество жилых районов (и стоимость жилого фонда в них) будут влиять близость к зонам промышленного производства, к центру города и к предприятиям торговли и культурно-бытового назначения. По-видимому, наиболее универсальный характер имеет концентрическая модель Барджеса. Остальные же модели можно рассматривать как её частные случаи (рис. 8).

Задачи выявления закономерности пространственных взаимодействий между системами городских поселений (перемещение людей, грузов, информации) привели исследователей к идее создания так называемых гравитационных моделей.

Гравитационными эта группа моделей называется потому, что они созданы по принципу закона всемирного тяготения, согласно которому два тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними. В гравитационных моделях в качестве массы обычно принимается численность населения.

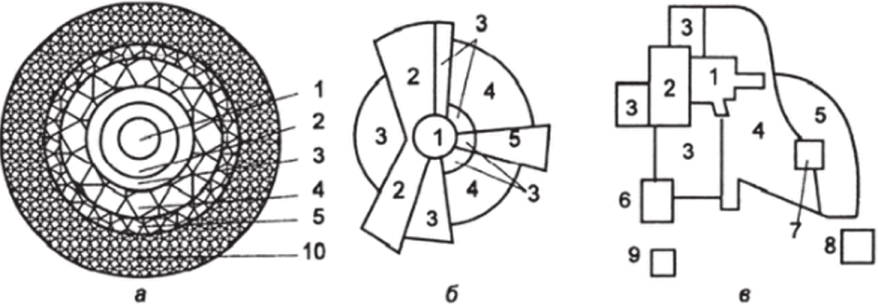
Рис. 8. Теоретические модели структуры юрода: концентрическая (а); секторная (6) н мноюндерная (в). Цифрами обозначены: 1 — центральный деловой район; 2- район оптовой горювлн и мелкие промышленные предприятия; 3 — район неблагоустроенных жилищ; ‘I — район жилищ среднею качества; 3 — район благоустроенных жилищ; 6 — район тяжелой промышленности; 7 — периферийный деловой район; 8 — жилые предместья; 9- промышленные предместья; 10- зона маят никовых миграций [2. -1,36].

Предложены способы дифференцированного учета исходных величии и параметров, вводимых в модели (взвешенные величины численности жителей в зависимости от размера дохода на душу населения в разных регионах, исчисление расстояния в стоимости затрат на переезд или перевозку грузов и т. д.). Исследование реальных условий взаимодействий между городами позволило выявить важное свойств!) относительного сжатия пространства между крупными городами, благодаря применению в сообщении скоростных транспортных средств (автомагистралей, самолетов, поездов, средств коммуникации и электронной связи). Крупные города как бы сближаются между собой, тогда как расположенные, казалось бы, ближе к ним малые города отдаляются.

Свойство динамичности также получило отражение в моделировании. Воздействие некоторых процессов, лежащих в основе развития города (например, диверсификации экономической деятельности), на взаимосвязанные с ним процессы (в частности, на сопутствующий рост населения и сферы обслуживания), можно количественно измерить, сделав определенные допущения и ограничения. Примером таких оценок является потенциал поля расселения городских поселений Московского региона [2,4, 28 и др.].

Наиболее интенсивно расселение в Московском регионе проходило в северо-восточном, северо-западном и южном направлениях. Эти же направления являются и зонами наиболее интенсивной маятниковой миграции [28].

Аналогичные подходы применены в ряде имитационных моделей, в частности, в динамической модели Дж. Форрестера [37]. Рассматривая город как сложную, во многом резистентную и относительно устойчивую систему, способную сопротивляться административным воздействиям и имеющую прямые и обратные связи, Форрестер пытается моделировать формирование и развитие города на протяжении длительного времени. Основные уровни модели Форрестера представлены на рис. 9. Подсистемы, выделенные в динамической модели Форрестера, включают население, жилой фонд и предприятия. Каждая подсистема рассматривается с точки зрения пространственно-временной эволюции. Население поделено на три класса: «Не полностью занятые», «Занятые» и «Менеджеры-профессионалы». В жилом фонде выделен «Дешевый жилой фонд», «Доходный жилой фонд» и «Сверхдоходный жилой фонд». Предприятия поделены на «Новые предприятия», «Зрелые предприятия» и «Предприятия, пришедшие в упадок» [37]. Функциональные связи между классами отражают тенденции развития основных градообразующих компонентов (рис. 9).

Согласно Форрестеру, развитие городской среды связано с развитием предприятий и при этом сопровождается изменением доходности жилого фонда и спросом на квалифицированные кадры. Когда новые предприятия только создавались, потребность в квалифицированных специалистахуправленцах была высока. Аналогично и стоимость жилого фонда возрастала, так как обладавшие высоким уровнем дохода топменеджеры были в состоянии её оплачивать.

Рис. 9. OciioniiMtf уровни и од см и Форрестера [37].

Но в случае, если через какое-то время предприятия оказывались в упадке, экономические трудности неизбежно сказывались и на трудовой занятости горожан, и на стоимости жилого фонда, которая, естественно, падала (рис. 9).

Следует отметить, что модель Форрестера представляет достаточно упрощённую картину городской системы, более свойственную моногородам. В модели, в частности, не учитываются финансовые отношения между органами власти и объектами управления. А ведь финансирование является основой проведения любых городских программ. Как правило, денежные средства поступают от других уровней власти в виде субсидий и дотаций, а также от населения, предприятий через налоги. Другим недостатком модели является ее сложность, многочисленность связей между переменными и множество допущений. В таких случаях результаты расчетов и адекватность самой модели реальным процессам вызывают большие сомнения. Кроме того, подобные имитационные модели основываются на исследовании ранее сложившихся тенденций и не учитывают возможных новых изменений. Такая условность ограничивает возможность их применения для анализа городских систем. Но, несмотря на подобные ограничения, модель Форрестера привлекла большое внимание искусством формализации многих процессов и параметров на основе системного анализа и программирования.

Контрольные вопросы:

• 1. Что такое городская система, каковы ее основные свойства?
• 2. Какие основные функции выполняют городские системы?
• 3. Можно ли рассматривать отдельный город как систему в большой системе городов?
• 4. Как использовать системный подход в анализе городских систем?
• 5. Как используется моделирование при изучении городских систем?
• 6. В чем основные различия моделей городских систем Кристаллера, Изарда и Форрестера?
• 7. Как изучается пространственная неравномерность городских систем?