Игры двух участников с противоположными интересами. 
Осторожные (минимаксные и максиминные) стратегии. 
Нижняя и верхняя цена игры. 
Седловая точка

Игру двух игроков с нулевой суммой назовем игрой с противоположными интересами или антагонистической игрой. Она имеет следующий вид: (5₁, 5₂;m₁,-m₁). Игроки являются чистыми антагонистами. В случае конечной игры с нулевой суммой достаточно знать одну из матриц — вторая матрица равна платежной матрице первого игрока, умноженной на -1: Ujj = ujj = —ufj. Поэтому такую игру можно описать одной матрицей:

Это матрица выигрышей первого игрока. Она же является матрицей проигрышей второго игрока.

Очевидно, антагонистические игры относятся к играм с полной информацией. Игра статическая, игроки одновременно выбирают свои стратегии. Первый выбирает строку, второй — столбец.

Пример 2.4. Рассмотрим антагонистическую игру двух игроков. Пусть матрица игры (выигрышей первого игрока) имеет вид.

Очевидно, какой бы столбец ни выбрал второй игрок, первому игроку стратегия а более выгодна, чем стратегия с. Поэтому достаточно рассмотреть только первые две строки матрицы:

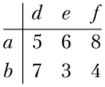
Заметим, что не только первый игрок вычеркивает третью строку, но и второй игрок сделает то же самое. Он может поставить себя на место первого игрока и увидеть, что а >- с.

Теперь же видно, что второму игроку, который минимизирует выигрыш первого, никогда не выгодно выбирать третью стратегию, поскольку его вторая стратегия в последней (усеченной) матрице игры при всех вариантах выбора первого игрока лучше третьей (е>- /). Следовательно, достаточно рассмотреть матрицу игры размерностью 2×2:

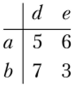
Заметим, что исключение вторым игроком стратегии /стало возможным только после исключения первым игроком стратегии с. В первоначальной матрице игры стратегия с была недоминируема.

В рассмотренном примере нам удалось уменьшить размерность игры до 2×2 за счет последовательного исключения заведомо невыгодных для игроков (строго доминируемых) стратегий. В дальнейшем мы научимся решать такие игры, т. е. находить равновесные стратегии игроков.

Будем полагать, что каждый игрок стремится обеспечить себе максимально возможный выигрыш при любых действиях противника — максимальный гарантированный выигрыш. Оптимальная стратегия первого игрока — это такая стратегия, которая обеспечивает ему максимальный гарантированный выигрыш при наихудших для него действиях противника:

При этом первый игрок рассуждает примерно так:

«Если я выберу г-ю стратегию s}, что соответствует г-й строке платежной матрицы, то мой противник, если бы он знал мой выбор (а он его не знает), выбрал бы такую стратегию (столбец), которая максимизировала его выигрыш, т. е. минимизировала мой выигрыш. Правда, он не знает, каков мой выбор, но может его угадать. Поэтому, будучи осторожным игроком, я буду считать, что он угадал и выбрал такую стратегию j» которая минимизирует мой выигрыш: иц. - min и_у. Таким образом, мой гарантированный.

^h i ¹

выигрыш при выборе мной г-й стратегии будет равен и_у = min и,. Понятно,.

' }

что я выберу такую стратегию (строку), при которой этот гарантированный выигрыш будет максимален, т. е. max min.

i j

Определение 2.6. Величина, а = max min называется нижней ценой игры. ' ^]

Аналогичные рассуждения в поведении второго игрока приводят к его оптимальной стратегии, определяемой из условия.

Определение 2.7. Величина Р = min max % называется верхней ценой.

/ i ^

игры. ^J

Минимаксная стратегия второго игрока гарантирует, что его проигрыш в игре не превысит верхнюю цену игры р.

Докажем, что нижняя цена игры в общем случае не превышает верхнюю (а < Р), т. е.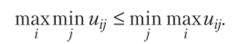

Имеем систем)' очевидных неравенств.

Поскольку в одном из этих неравенств в левой части достигается.

max min и_ц, то отсюда следует неравенство max min щ < min max u,_r

ij ijji

Максиминная стратегия первого игрока и минимаксная стратегия второго игрока называются осторожными стратегиями.

Если верхняя и нижняя цены равны (тахпнпм, =minmaxw, =м,),.

i j j i

то игроки получат свои гарантированные платежи. Платежная матрица в этом случае имеет седловую точку — профиль стратегий, в котором получен элемент щ, минимальный в строке и максимальный в столбце, м_у называют ценой игры.

Пример 2.5. Рассмотрим матричную игру.

Справа в каждой строке запишем min u_ir а снизу в каждом столбце запишем max И;.-:

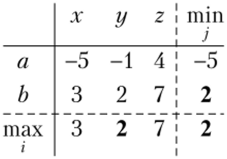
i ^J

Очевидно, элемент второй строки, второго столбца является седловой точкой.

Здесь, а = Р = 2 — цена игры. Оптимальными стратегиями игроков являются: стратегия Ъ первого игрока и стратегия у второго игрока. Профиль стратегий (Ь;у) — седловая точка.

Удобно отмечать подчеркиванием максимальные элементы в каждом столбце и надчеркиванием минимальные элементы в каждой строке:

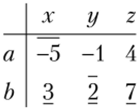
Тогда, если существует элемент, одновременно и подчеркнутый, и надчеркнутый, то соответствующие ему стратегии являются седловой точкой. Решить игру — значит найти седловую точку.

Игра двух участников с нулевой суммой, имеющая седловую точку, называется вполне определенной. Для вполне определенных игр имеем.

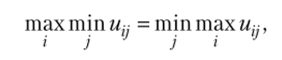
т.е. нижняя цена игры равна верхней.

Однако не любая матричная игра имеет седловую точку.

Пример 2.6. Пусть имеется антагонистическая игра двух игроков А и В. Игрок А выбирает строки, игрок В — столбцы. Матрица выигрышей первого игрока имеет вид.

Справа в каждой строке запишем min u_jjy а снизу в каждом столбце запишем max Ujj:

Максиминная стратегия первого игрока (А) даст элемент max min и, =.

' j

= U2= 1, в то время как минимаксная стратегия второго игрока (В) даст.

min max w₇ = и_2?1 =5. В этом случае имеем строгое неравенство: j i ^J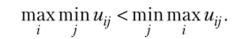

Такая игра относится к классу неполностью определенных игр. Пусть для определенности платежная матрица задана в рублях. Придерживаясь стратегии а, игрок А ожидает, что игрок В выберет стратегию у, т. е. игрок А получит 1 руб. Придерживаясь стратегии z, игрок В ожидает, что игрок А выберет стратегию Ь, т. е. игрок В проиграет 5 руб. В результате же при выборе игроком А стратегии а и игроком В стратегии z результат платежа равен 4, чего не ждал ни один из них.

Минимаксная и максиминная стратегии в неполностью определенных играх неустойчивы. Пусть игра повторяется многократно. Если игрок А выбирает ход я, то игрок В, «привыкнув» к этому выбору игрока А, скоро откажется от хода z и выберет ход у. Игрок А, «привыкнув» к этому выбору игрока В, откажется от хода я и выберет ход b и т. д. Положение, в котором игроки используют минимаксные (максиминные) стратегии, оказывается в таких играх неустойчивым и может быть нарушено, как только одному из игроков становится известна стратегия соперника. Данный подход (выбор осторожных стратегий) неприемлем в неполностью определенных играх.

Напротив, вполне определенные игры устойчивы: если один из игроков придерживается своей минимаксной (максиминной) стратегии, то другому не удастся увеличить свой выигрыш, отступая от своей максиминной (минимаксной) стратегии.

На следующем примере покажем, как можно использовать условие, при котором некоторые из стратегий оказываются доминируемыми.

Пример 2.7. Рассмотрим игру двух игроков с нулевой суммой и следующей платежной матрицей:

Пусть а, Ь, с — стратегии первого игрока, а х, у, z, t— стратегии второго игрока. Очевидно, что для второго игрока (для него это матрица проигрышей!) стратегия t строго доминирует стратегию у, а стратегия z строго доминирует стратегию х. Поэтому стратегии у их можно не рассматривать — они играться не будут. Причем к этому выводу приходят оба игрока (первому игроку достаточно поставить себя на место второго). Платежная матрица примет вид.

Теперь видно, что для первого игрока стратегия а строго доминирует с. Платежная матрица поэтому примет вид.

В полученной игре нижняя цена игры равна 1, а верхняя цена равна 2. Поскольку 2 > 1, данную игру следует отнести к классу неполностью определенных игр.

Описанная в предыдущем примере процедура исключения строго доминируемых стратегий не может привести к исключению из рассмотрения седловых точек. Если же ее заменить процедурой исключения доминируемых стратегий, то это может привести к исключению седловых точек. Например, в матричной игре.

четыре седловые точки: (а> х); (а, 2); (b, х) (b, г). Однако процедура исключения доминируемых стратегий может привести к исключению двух из них. Действительно, стратегии второго игрока г/, 2 и t доминируемы стратегией х. Исключая их, получим матрицу.

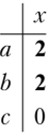
Далее, исключая доминируемую третью стратегию первого игрока, получим.

Две из четырех седловых точек оказались исключенными методом итерационного исключения доминируемых стратегий. Если ставить задачу отыскания какой-нибудь седловой точки, то этот метод приемлем. Если же требуется отыскать все седловые точки, то следует исключать только строго доминируемые стратегии.

Пример 2.8 («Игра полковника Блотто»). Две воюющие армии ведут борьбу за два пункта. Первая армия под командованием полковника Блотто состоит из четырех полков; вторая иод командованием капитана Киже состоит из трех полков. Армия, которая посылает больше полков на тот или иной пункт, занимает его и уничтожает все направленные на этот пункт силы противоположной стороны, получая единицу как за занятый пункт, так и за каждый уничтоженный полк противника. Полковник Блотто должен решить, как распределить силы, для того чтобы выиграть как можно больше очков. Требуется построить матрицу игры и выяснить, какова верхняя и нижняя цена игры.

Решение

Полковник Блотто может распределить свои полки пятью способами. Соответственно, у него имеется пять чистых стратегий. Стратегии могут быть представлены как пары чисел (х 4 — х), где х е {0; 1; 2; 3; 4} — число полков, посылаемых на пункт 1, а 4 — х — число полков, посылаемых на пункт 2. Аналогично можно представить стратегии капитана Киже: (г/; 3 — г/), где у е {0; 1; 2; 3}. Далее строим матрицу выигрышей. Пусть, например, игроки выбирают стратегии (3; 1) и (2; 1). Тогда пункт 1 будет захвачен полковником Блотто, и он получает 1 за захваченный пункт и 2 за уничтожение двух полков противника. Итого результат равен 3. В пункте 2 равновесие войск и никто ничего не получает.

Приведем матрицу выигрышей:

Для нахождения верхней и нижней цены подчеркнем максимальные элементы в каждом столбце матрицы и надчеркнем минимальные элементы в каждой строке:

Верхняя цена игры равна 3, а нижняя цена игры равна 0. Как видим, седловой точки нет, и игра относится к классу неполностью определенных игр. В следующем параграфе рассматривается, как решаются такие игры.