Кривые роста и их свойства

Кривые роста, описывающие закономерности развития явлений во времени, получают путем аналитического выравнивания временных рядов. Они представляют однофакторные модели прогнозирования; фактором выступаст время. Выравнивание ряда с помощью тех или иных функций в большинстве случаев оказывается удобным средством описания эмпирических данных, характеризующих развитие во времени исследуемого явления. Использованию кривых роста должен предшествовать содержательный анализ явления с целью выяснения возможности экстраполирования тенденций.

Кривые роста часто используются в исследовании динамики реальных процессов различной природы. Они применяются при анализе миграционных процессов в человеческом и биологических сообществах Аналитическое выравнивание состоит из следующих этапов:

• 1) выбор типа кривой, форма которой соответствует характеру изменения временного ряда;
• 2) определение численных значений (оценивание) параметров кривой.

Найденная функция позволяет получить выравненные уровни ряда. Выбор типа кривой предполагает знакомство с основными видами кривых и изучение их основных свойств. Основной интерес представляют преобразования приростов, которые можно представить в виде линейной функции. Эти характеристики используются при выборе вида кривой роста.

Основные типы кривых роста подробно описаны и иллюстрированы графически в монографии Е. М. Четыркина (9):

• 1. Полиномы (многочлены).
• 2. Экспоненты.
• 3. Логистические кривые.

Общий вид многочлена :

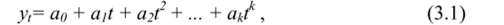
где а_п, Ц/, «2, … — параметры многочленов, t — независимая переменная, к — показатель степени многочлена. Параметры полиномов невысоких степеней могут быть интерпретированы в зависимости от содержания ряда динамики. Их можно характеризовать как: параметр ао — уровень ряда при t= 0, параметр а/ - скорость роста, параметр а2 — ускорение роста, параметр а? — изменение ускорения.

Действительно, полином первой степени на графике представляет прямую, т.с. предполагается постоянство приростов ординат.

Линейная зависимость может иметь место в процессах экстенсивного развития, однако это нс может происходить в течение длительного периода. Со временем скорость изменяется и либо происходит ускорение, либо спад.

Полином второй степени характеризует динамику с равномерными приростами, положительными для одной ветви параболы и отрицательными для другой. Легко показать, что приросты (первые конечные разности ординат параболы) могут быть охарактеризованы уравнением прямой:

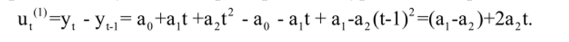
Соответственно приросты второго порядка (вторые разности) постоянны:

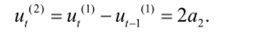
Парабола второй степени применима для описания процессов, характеризующихся равноускоренным ростом или равноускоренным снижением. Если параметр а:>0, то ветви направлены вверх, функция имеет минимум. Если ci2< 0, то ветви направлены вниз и парабола имеет максимум. Параметры ао и а/ нс влияют на форму кривой, а только определяют ее положение в пространстве.

У параболы третьей степени знак прироста ординат может меняться один или два раза. Первые разности ординат при нанесении на график представляют собой ординаты параболы второго порядка, т. е.

Ятппкте пячнпгти ичмрнякугся ЛИНеЙНО!

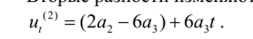
Разности третьего порядка являются постоянными:

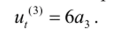
Простая экспоненциальная кривая является показательной функцией и имеет следующий вид:

Кривая характеризуется постоянными темпами роста и прироста. Темп роста будет равен.

темп прироста равен.

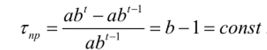. Если b> 1, то функция является возрастающей с ростом t и убывающей при 6<1. Логарифмирование обеих частей функции (3.2) приводит к линейной зависимости от (:

После обозначения or = loga и /3 = logb получаем:

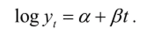
Экспоненциальный характер наблюдается после достижения определенного уровня присуще многим процессам при достижении определенного уровня Более сложной является зависимость, называемая логарифмической параболой:

Логарифмирование обеих частей выражения приводит к виду: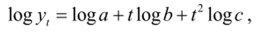

называемому логарифмической параболой. Темп прироста этой кривой равен отношению первой производной к ординате (7, с.24). Поэтому темп прироста примет вид:

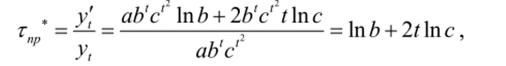
т.е. темп линейно зависит от времени.

Многочлены не имеют асимптот, а экспоненциальная и логарифмическая параболы имеют асимптоты. У экспоненциальной кривой y_t-> 0 при t->-оо, если b> 1, и y_t —" 0 при / —> оо, если b< 1.

Достаточно часто динамика социальноэкономических процессов такова, что наблюдается тенденция замедления темпов роста и имеет место насыщение. Например, расходы домохозяйств на продукты питания по мере роста доходов характеризуются насыщением. В таких случаях кривая должна иметь асимптоту, отличную от нуля. Такому условию удовлетворяет модифицированная экспонента. имеющая вид:

Кривая отличается от обычной экспоненты сдвигом по оси ординат на величину к, поэтому имеет горизонтальную асимптоту у = к, ее линия стремится к асимптоте либо при t —" со, либо при t —> -со. Параметр а равен разности между ординатой кривой (при t — 0) и асимптотой. Если параметр а отрицателен, то асимптота находится выше кривой, если а положителен, то асимптота проходит ниже ее. Параметр b равен отношению последовательных приростов. Чаще всего встречается кривая с параметрами а <0 и Ь<1.

Особенность модифицированной экспоненты заключается в том, что отношения последовательных приростов при равномерном распределении ординат по оси времени постоянны:

А логарифмы приростов ординат кривой линейно зависят от переменной t. Действительно,.

Откуда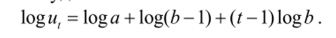

В демографических расчетах и некоторых расчетах в области страхового бизнеса используется S — образная кривая, или кривая Гомперца:

11аиболынсс применение находит кривая, у которой log, а < 0 и b < 1. Траектория кривой имеет четыре различных этапа. На первом этапе прирост медленно увеличивается с ростом t , затем скорость возрастает, затем после прохождения точки перегиба приросты начинают уменьшаться и, наконец, вблизи от асимптоты приросты снова замедляются.

Кривая Гомперца имеет особенность: отношение последовательных приростов ординат в логарифмах постоянно.

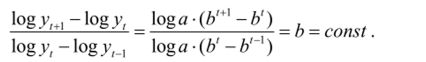
Логарифмирование выражения (3.5) приводит к известной модифицированной экспоненте:

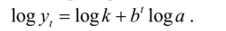
Для нахождения линейного преобразования характеристик приростов и уровней относительно t можно определить темп прироста с помощью производной:

Логарифмирование полученного результата дает линейное выражение: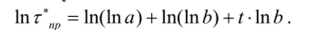

Если в модифицированной экспоненте (3.4) y_t заменить обратной величиной —, то преобразованное выра;

У, жение дает логистическую кривую:

Логистическая кривая, или кривая Перла-Рида записывается в виде:

где е- основание натуральных логарифмов, /(/) — функция от /, например, /(/) = -at. Тогда.

Если Ь=1, а вместо основания натуральных логарифмов взять основание десятичных логарифмов и положить f (t)-a + bt, то получится логистическая кривая, центрально симметричная относительно точки перегиба:

При t —> -со ордината стремится к нулю, а при t —> +оо ордината стремится к асимптоте. Если взять вторую производную от у, по времени для функции (3.8) и приравнять се нулю, то местоположение точки перегиба кривой t = In b: а, в этой точке у, = к 2

Преобразование приростов и ординат кривой, линейное относительно /, находится вычислением производной функции (3.8):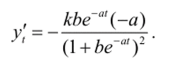

Полученное выражение легко приводится к линейному относительно / делением на у,² и логарифмированием полученного результата: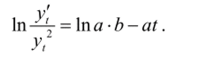

Рассмотренные кривые могут описывать процессы технологического развития, расширения товарных рынков, реализации инвестиционных проектов.