Понятие простого и сложного процента

Различие простых и сложных процентных ставок связано с выбором исходной базы для начисления процентов. Если ставка процентов применяется к одной и той же начальной сумме на протяжении всего срока ссуды, то используемая ставка называется простой.

Пусть Р — первоначальная сумма, i — ставка процентов в виде десятичной дроби, 5 — наращенная сумма, /- проценты за весь срок. Изменение суммы долга с начисленными простыми процентами на одну и ту же исходную сумму Р описывается арифметической прогрессией:

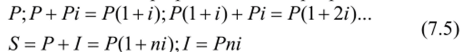
(1 + ш) — множитель наращения при начислении простых процентов.

Таким образом, сумма долга при простом проценте линейно зависит от процентной ставки. Графически это будет иметь вид (ряд 3):

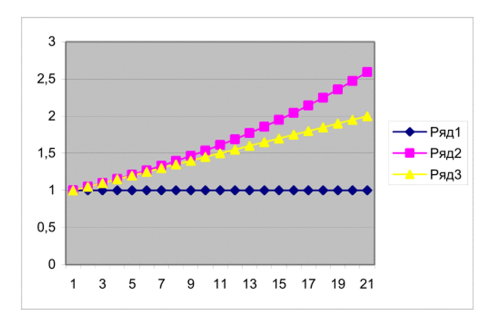
Рис. 7.1 Множители наращения по равным сложной и простой ставке.

При начислениях по сложной процентной ставке база увеличивается с каждым шагом во времени. Наращение по сложным процентам можно представить как последовательное реинвестирование средств, вложенных под простые проценты, на один период начисления. Присоединение начисленных процентов к сумме, которая служила базой для их определения, называется капитализацией процентов.

Изменение суммы долга в данном случае представляет геометрическую прогрессию:

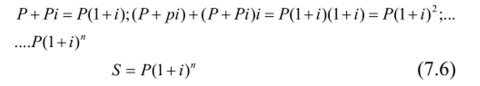
(1 + /)" - множитель наращения при начислении сложных процентов.

Соотношение значений множителей наращения по равным простой и сложной процентным ставкам и одинаковой абсолютной величине зависит от срока ссуды. Для срока менее Нода 1 + л/ > (1+с,)", а для срока более 1 года ¹+ 0+U*;

Исходя из вида процентной ставки, различают математическое дисконтирование и банковский коммерческий учет. Математическое дисконтирование представляет решение задачи, обратной наращению первоначальной суммы ссуды, депозита и т. д.: какую первоначальную сумму надо выдать в долг, чтобы при начислении на нес процентов по ставке г к концу срока получить наращенную сумму, равную 5. Решив уравнение (7.5) относительно Р, получим:

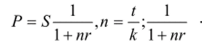 — дисконтный множитель, показывающий какую долю составляет Р в величине S. Разность S-D можно рассматривать нс только как проценты, начисленные на Р, но и как дисконт суммы S.

При банковском учете банк или другое финансовое учреждение до наступления срока платежа по векселю или другому платежному обязательству, покупает его у владельца по цене, меньшей той суммы, которая должна быть выплачена по нему в конце срока, т. е. приобретает или учитывает его с дисконтом.

Владелец векселя с помощью его учета имеет возможность получить деньги ранее указанного на нем срока. При учете векселей применяется банковский или коммерческий учет. Согласно этому методу проценты за пользование ссудой начисляются на сумму, подлежащую уплате в конце срока ссуды. При этом применяется учетная ставка cl. Простая годовая учетная ставка находится как d = (S- P)/S, в то время как простая ставка процентов г = (S-Р)/Р. Отсюда Р = S (l-nd), где (1 -nd) — дисконтный множитель, и — продолжительность срока в годах от момента учета до даты уплаты по векселю.

Учетная ставка отражает фактор времени более жестко. При n>l/d величина Р станет отрицательной, чего нс может случиться при математическом дисконтировании; при любом сроке современная стоимость >0.