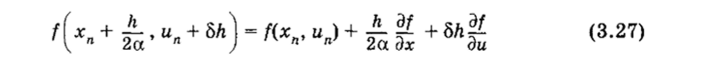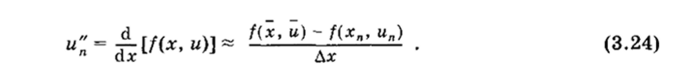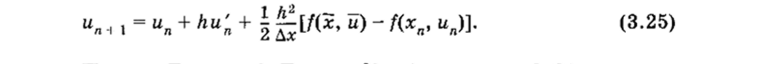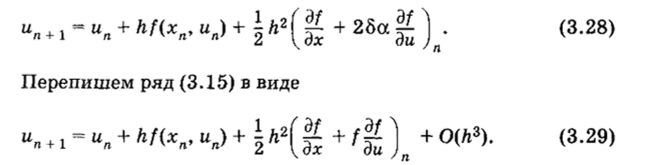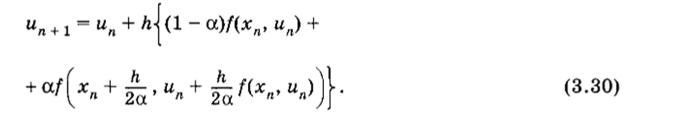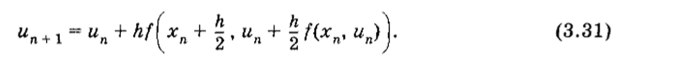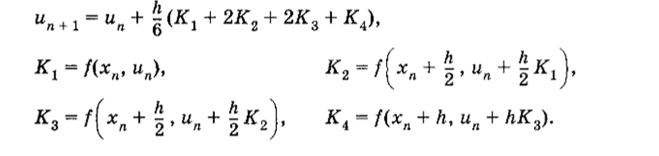Метод Рунге — Кутты

Метод Рунге — Кутты позволяет строить схемы различного порядка точности. Основная идея метода состоит в построении специального алгоритма — такого, чтобы приращение функции на шаге Дц = и_{п +} j — и_п совпадало с приращением Ди, которое определяется из ряда Тейлора (3.15) с учетом возможно большего числа членов. При этом вторые и следующие производные определяются не дифференцированием, а путем многократного вычисления функции f (x, и) в некоторых промежуточных точках между x_nn х_{п + г}

Проиллюстрируем основные идеи метода на примере получения схем второго порядка точности.

Оставим в разложении (3.15) члены вплоть до 0(Л²), имея в виду, что последний член разложения соответствует предполагаемому порядку точности схемы. Имеем.

Чтобы избежать явного дифференцирования, заменим вторую производную и" в соотношении (3.23) разностью.

Величины х, й и Ах подбираются так, чтобы обеспечить нужный порядок точности. Подставляя выражение (3.24) в (3.23), получаем.

Полагая х = х_п + yh, и = и_п + Oh, обозначая, а = Л/2Ах и имея в виду, что Ах = х — х_п, и, следовательно, у = ½а, а также учитывая, что и'_п = f (x_n, и_п), переписываем выражение (3.25) в виде.

Параметры, а и 5 определяются из условия наилучшего соответствия выражения (3.26) ряду (3.15). Принимая и подставляя соотношение (3.27) в (3.26), имеем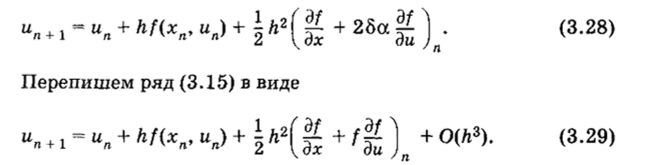

Из сравнения формул (3.27) и (3.29) видно, что первые три члена в этих формулах совпадают, если а5 = f{x_n, и_п)/2. Выражая 6 через а и подставляя в (3.26), получаем однопараметрическое семейство разностных схем Рунге — Кутты второго порядка точности. В результате.

Схема (3.30) при, а * 0 имеет третий порядок точности на шаге и второй на интервале. Из (3.30) можно получить все рассмотренные разностные схемы. Так, при, а = 0 имеем метод Эйлера, выражаемый формулой (3.16а), при а = ½ — первую итерацию метода Эйлера с пересчетом, которому соответствует формула (3.19), а при, а = 1 — так называемый метод хорд, которому соответствует соотношение.

Аналогичным образом могут быть получены и схемы Рунге —Кутты более высокого порядка точности. В настоящее время наиболее распространены схемы четвертого порядка точности. Например, схема Рунге — Кутты четвертого порядка точности, которая используется в большинстве стандартных программ на компьютерах, имеет вид.