Формулы численного интегрирования

Заменим подынтегральную функцию, входящую в (2.50), интерполяционным многочленом Лагранжа нулевой степени, проходящим через середину отрезка — точку х = (а + Ь)/2 (рис. 2.5). Площадь криволинейной трапеции можно заменить площадью прямоугольника, т. е.

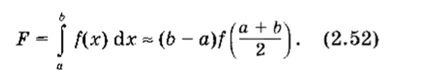
Формула (2.52) носит название ФОРМУЛЫ ПРЯМОУГОЛЬНИКОВ или ФОРМУЛЫ СРЕДНИХ. Ее погрешность составляет.

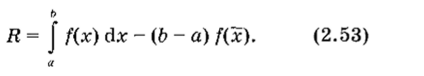
Разложение функции f (x) в ряд относительно середины отрезка имеет вид.

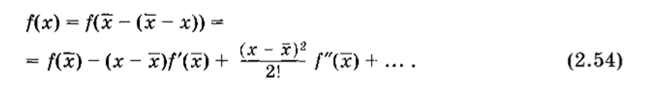
Подставив выражение (2.54) в (2.53), получим.

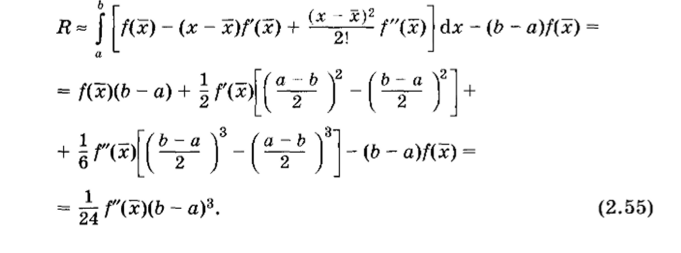
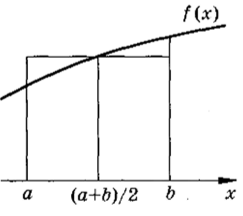
Рис. 2.5.

При вычислении ошибки интегрирования уничтожился не только первый, но и второй член разложения, что связано с симметричным выбором узла интегрирования. И хотя по построению формула точна для многочленов нулевого порядка, выбор симметричного узла интерполяции привел к тому, что формула точна для любой линейной функции.

Значение остаточного члена в формуле прямоугольников (2.53) может быть велико, так как разность (6 — а) может быть достаточно большой. Для повышения точности введем сетку.

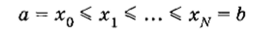
с достаточно мелким шагом h_t = jc₍ — x_t _ j и применим формулу прямоугольников на каждом шаге сетки. Тогда получим обобщенную формулу прямоугольников.

с величиной остаточного члена.

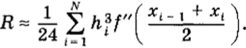
На равномерной сетке с шагом h_t «= х₍ — x_t _ j = const формула (2.56) упрощается и имеет вид.

величина остаточного члена составляет Заменяя в (2.58) сумму интегралом, получаем.

Для справедливости оценки остаточного члена (2.58) необходимо существование непрерывной второй производной; если вторая производная f’x) — кусочно-непрерывная, то удается сделать лишь мажорантную оценку, заменяя f" (x) ее максимальной величиной на [а, 6]. Тогда, если обозначить М₂ = max | f" (x) |_[а остаточный член.

В том случае, когда функция f (x) задана в виде таблицы, ее значение в середине интервала неизвестно. Это значение находится, как правило, интерполированием, что приводит к ухудшению точности формулы.

В случае таблично заданных функций удобно в качестве узлов интерполяции выбрать начало и конец отрезка интегрирования, т. е. заменить функцию f (x) многочленом Лагранжа первой степени. Имеем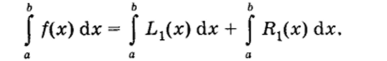

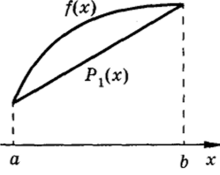
Рис. 2.6.

В этом случае величина интеграла, равная площади криволинейной трапеции, приближенно заменяется величиной площади трапеции (рис. 2.6). Поэтому получаем.

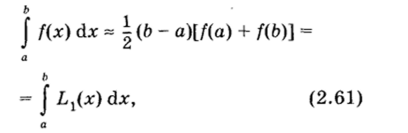
имея в виду, что х₀ = а, х_г = Ь. Эта формула носит название ФОРМУЛЫ ТРАПЕЦИЙ. При использовании формулы трапеций для.

ь

оценки погрешности интегрирования вычислим J dx по.

а

формулам (2.18). Имеем.

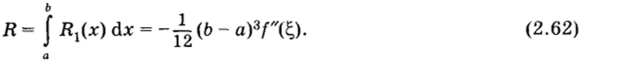
Погрешность формулы трапеций вдвое больше погрешности формулы прямоугольников. Это объясняется тем, что выбор в формуле прямоугольников в качестве узла интерполяции симметричного узла приводит к повышению ее точности.

Для повышения точности формулы (2.61) введем на отрезке [а, Ь] сетку.

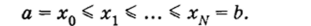
Подсчитывая значение интеграла для каждого интервала и суммируя эти значения, получаем обобщенную формулу трапеций.

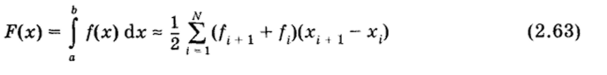
со значением остаточного члена.

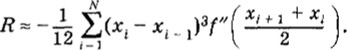
Эти формулы упрощаются на сетке с постоянным шагом Л = Л₍ = Xj — д, _t = const (i — 0, 1, - 1):

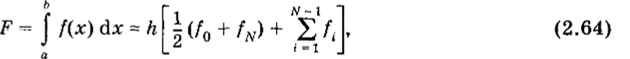
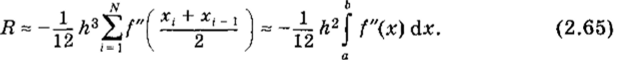
Введем обозначение М₂ ~ max |ГХ^)1(а &]• На практике пользуются мажорантной оценкой величины остаточного члена.

Таким образом, формула трапеций (как и формула прямоугольников) имеет второй порядок точности относительно шага сетки, и погрешность асимптотически стремится к нулю при h —" 0 с точностью до членов более высокого порядка малости.

Для повышения порядка точности формулы численного интегрирования заменим подынтегральную кривую параболой — интерполяционным многочленом Лагранжа второй степени, выбрав в качестве узлов интерполяции концы и середину отрезка интегрирования: х₀ = а, х_х ~ (а + Ь)/2, х_г = Ъ (рис. 2.7).

В этом случае, проинтегрировав интерполяционный многочлен для равноотстоящих узлов, получим.

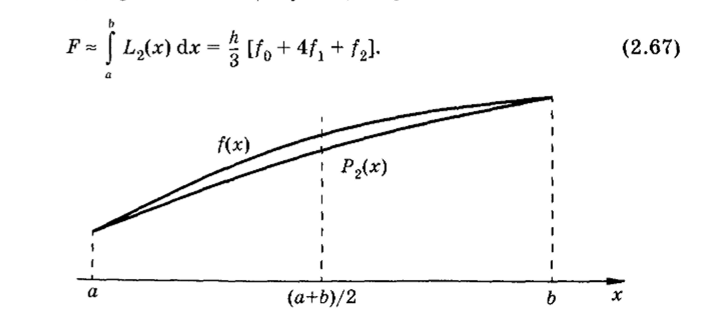
Рис. 2.7.

ь

При этом значение остаточного члена R ~ J Д₂(х) dx оценивается приближенным соотношением °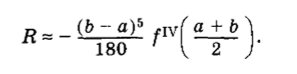

Формулу (2.67) называют ФОРМУЛОЙ СИМПСОНА. Для неравноотстоящих узлов х₀, Xj, х₂ величина F составляет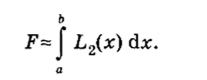

Как и в предыдущих двух случаях, для повышения точности формулы (2.67) введем сетку с достаточно малым шагом. Суммируя значения нтегралов, полученных по (2.67) для каждого интервала, получаем обобщенную формулу Симпсона (парабол), которая на равномерной сетке имеет вид.

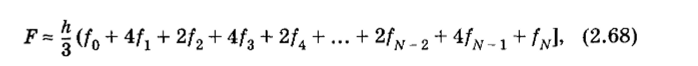
а величина остаточного члена —.

Таким образом, формула парабол имеет четвертый порядок точности относительно шага сетки. Введем обозначение М₄ = = max |/^IV(x)|_{[o 6}j. Как правило, для оценки величины погрешности применяют мажорантную оценку.

Количество интервалов N, на которое делится отрезок интегрирования, должно быть всегда четным, так как интерполяционный многочлен второй степени проводится через три точки.

СИМПСОН ТОМАС (Simpson Thomas; 1710—1761) — английский математик, ряд работ которого посвящен элементарной геометрии, тригонометрическому анализу и математическому анализу. В 1743 г. С. вывел формулу приближенного интегрирования (формулу Симпсона).