Анализ процессов в простейшей статической САР в динамическом режиме

Рассмотрим, каким образом можно математически описать анализируемую статическую систему регулирования (см. рис. 1.3) в динамическом режиме. Для упрощения аналитического описания в качестве регулирующего параметра будем пользоваться значением статической ошибки /г, имея в виду, что понятие «ошибка» можно отнести только к уровню жидкости, но не к значению Q", которое система отрабатывает без ошибки, и в отработке этого значения и состоит назначение рассматриваемой системы. В связи с этим заменим термин «статическая ошибка» термином «статическое отклонение».

Изменение (уменьшение) объема AV жидкости за время At при разных значениях Q_p и Q_n выражается формулой.

При этом уровень жидкости II уменьшается, а отклонение h увеличивается на величину %/

где S — площадь резервуара.

Из формулы (1.8) выразим отношение приращения отклонения Ah уровня жидкости к отрезку времени At, за который происходит это отклонение:

или, переходя к пределу при Af —>0, получим производную отклонения h по времени:

Подача Q_n жидкости, осуществляемая задвижкой, прямо пропорциональна отклонению h:

где k — коэффициент пропорциональности или передаточный коэффициент задвижки. Такая прямая пропорциональность (1.11) называется законам регулирования по отклонению и является простейшим видом закона регулирования.

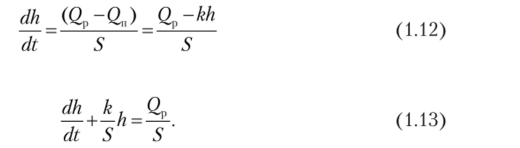
Подставив значение Q, из формулы (1.11) в формулу (1.10), получим или Запишем уравнение (1.13) в виде Обозначим

и назовем эту величину, имеющую размерность времени, постоянной времени САР. Тогда дифференциальное уравнение (1.14) будет иметь вид.

В стационарном режиме, когда dh/dt = 0, отклонение h выражается уравнением прямой линии (рис. 1.5, 6):

Дифференциальному уравнению (1.16), как известно из курса «Теория линейных электрических цепей», соответствует характеристическое уравнение Тр + 1=0, корень которого р = -1 /Т. В нестационарном (переходном) режиме аналитическое решение дифференциального уравнения (1.16) будет иметь вид Здесь А — постоянная интегрирования, определяемая из начальных условий (НУ). Например, если в начальный момент времени при t — 0 отклонение h также было равно нулю, то.

и уравнение (1.18) примет вид.

Здесь е = 2,718 — основание натурального логарифма.

Как следует из уравнения (1.20), в случае переходного процесса от значения, когда расход жидкости Q_p = 0 и отклонение h — 0, к значению Q_p * 0 увеличение, А произойдет нс мгновенно, а по прошествии некоторого времени, в течение которого будет происходить переходный процесс. При этом отклонение h будет меняться по экспоненциальному закону и через время, равное Т, достигнет значения, равного 1 — е^-1 = 0,632 от значения Qp/k (рис. 1.7). Чем больше постоянная времени Т, тем более полого пойдет кривая и тем длительнее будет переходный процесс установления выходной величины. Это значит, что постоянная времени Т характеризует инерционность системы. Считают, что переходный процесс заканчивается через время, равное 3Т.

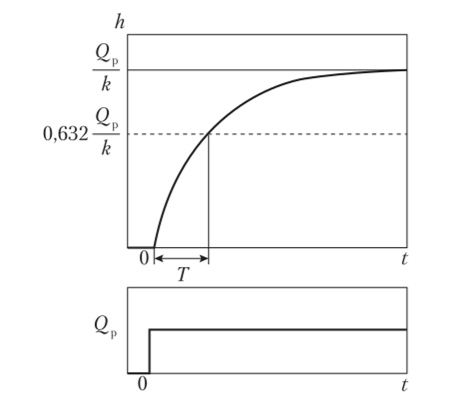
Рис. 1.7. Переходный процесс при скачкообразном изменении расхода жидкости.

Характеристику, изображенную на рис. 1.7, при воздействии скачкообразного напряжения, называют переходной характеристикой. Чем больше время переходного процесса при скачке входной величины, тем более инерционной считается САР или ее отдельное звено. Инерцию системы при отработке возмущения характеризует постоянная времени Т. Как следует из выражения (1.15), инерция системы прямо пропорциональна площади резервуара и обратно пропорциональна коэффициенту пропорциональности k.

Заметим, что вместо дифференциального уравнения динамики САР (или в нашем случае одного звена) пишут так называемую передаточную функцию звена. Ее получают следующим образом. В уравнении (1.16) заменяют переменную h ее изображением по Лапласу h (p), а дифференцирование изображения заменяют умножением изображения h (j>) на оператор р.

Замечание 1.3.

Изображения по Лапласу как функции оператора р записываются прописными буквами. Поскольку прописная буква Н используется для обозначения уровня жидкости, изображение переменной h записывается строчной буквой.

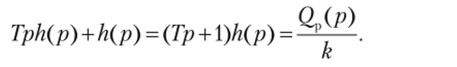
Тогда передаточная функция W (p) САР, равная отношению изображения выходной величины к изображению входной величины, будет иметь вид.

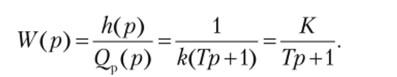
Здесь К = 1/ k — передаточный коэффициент системы автоматического регулирования по отклонению уровня жидкости в резервуаре. Действительно, поскольку выходной величиной САР является отклонение /г, то согласно формуле (1.17) отношение h/Q_p = /k = К.

Полученная передаточная функция характеризует инерционное звено первого порядка. Целесообразность введения такой функции будет показана ниже.

Анализ переходных процессов с помощью решения дифференциальных уравнений удобно проводить в интегрированном пакете MathCad 1231. Дифференциальное уравнение в этом случае записывается в форме Коши:

На рис. 1.8 показано решение дифференциального уравнения (1.21) в интегрированном пакете MathCad численным методом Рунге — Кутта с помощью функции rkfixed (решение методом Рунге — Кутта четвертого порядка с фиксированным шагом). В скобках функции rkfixed через запятые перечисляются: начальные условия А, начальная (0) и конечная (100) точки интервала интегрирования, выраженные в минутах, число точек п (1000), не считая нулевой точки, и первая производная искомой функции (D). В функции первой производной D (t, h) в скобках указывается сначала переменная, по которой берется производная (в нашем случае это t), и через запятую указывается функция, от которой берется производная (в нашем случае это h).

Решение получается в виде матрицы Z из двух столбцов, содержащих п строк. Первый столбец матрицы (Z_n0) содержит точки t_n, в которых ищется решение дифференциального уравнения, второй столбец (Z_n,) содержит результаты решения — значения найденного отклонения h_n в заданных точках.

На рис. 1.8 выражение (10 — h_n) на оси ординат графика соответствует уровню Я жидкости в резервуаре, а выражение Q_p(h_n)/10 — уменьшенному в 10 раз расходу жидкости. Под каждым выражением для изображаемой величины показан стиль линии, которой будет изображаться данная величина. Это необходимо для того, чтобы знать, какой линией изображается каждая кривая, когда на графике изображается несколько кривых.

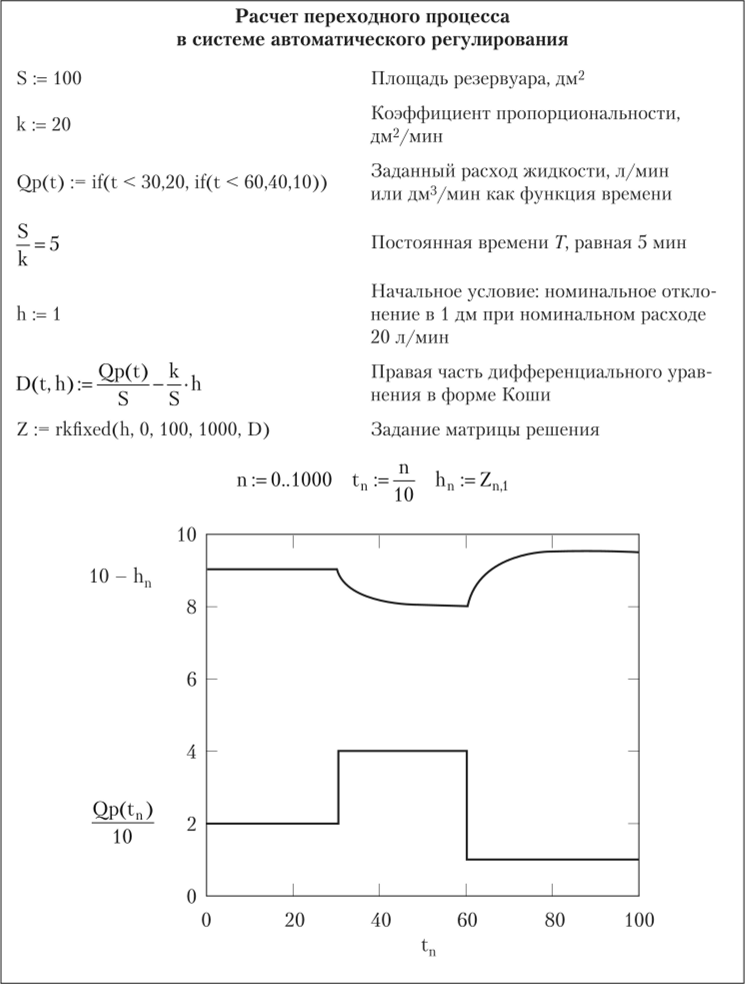
Рис. 1.8. Пример решения уравнения (1.21) в интегрированном пакете MathCad:

верхняя кривая — уровень Н жидкости в резервуаре (10 — h") нижняя кривая — уменьшенный в 10 раз расход жидкости (<2_p(f")/10).

На рис. 1.9 график приведен с указанием масштабных линеек для каждой величины. Решение уравнения (1.21) было выполнено для следующих данных: площадь резервуара 5 = 100 дм²; коэффициент пропорциональности k = 20 дм²/мин; номинальный расход жидкости Q_p = 20 дм³/мин.

(л/мин); уровень жидкости при ее нулевом расходе Н₀ = 10 дм; отклонение при номинальном расходе h — 1 дм. При этих данных постоянная времени Г = 5/? = 100/20 = 5 мин.

На рис. 1.10 показан переходный процесс, когда площадь резервуара уменьшена и составляет 20 дм². В этом случае постоянная времени Т = 1 мин, объект регулирования становится менее инерционным, и процесс регулирования идет значительно быстрее.

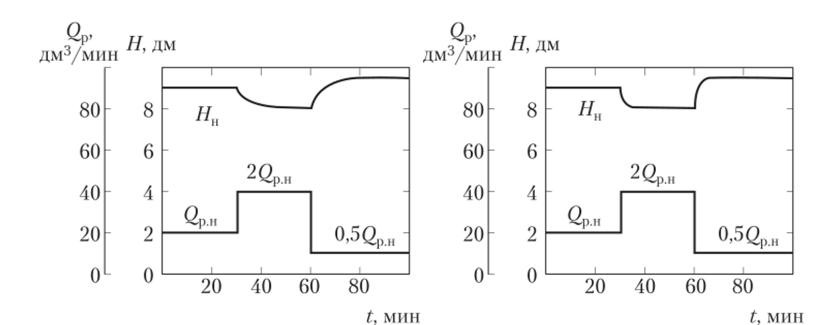
Рис. 1.9. График переходного процесса с указанием масштабных линеек при Т = 5.

Рис. 1.10. График переходного процесса с указанием масштабных линеек при Т = 1.

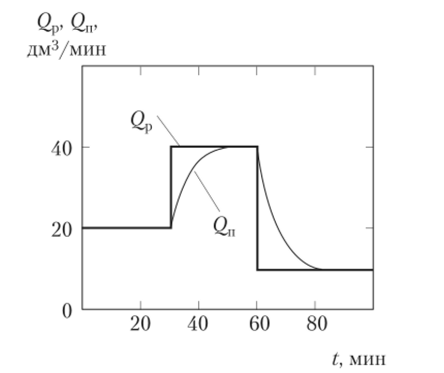
Рис. 1.11. Изменение подачи жидкости при изменении ее расхода.

На рис. 1.11 показано изменение подачи жидкости при изменении ее расхода. Как следует из рис. 1.11, при автоматическом регулировании подача жидкости в переходном режиме изменяется, но экспоненциальному закону, т. е. она повторяет расход с некоторой инерционностью. Процесс, представленный в виде графика на рис. 1.11, называют кривой процесса регулирования. Кривые процесса регулирования показывают, насколько хорошо данная система автоматического регулирования справляется со своей задачей.