Методы решения задач упорядочения альтернатив-решений на основе нечетких отношений предпочтения

Многие задачи упорядочения (задачи класса А) математически могут быть описаны множеством допустимых выборов (альтернатив) и заданным на этом множестве отношением предпочтения, которое отражает интересы ЛПР. Как правило, это отношение бинарное, т. е. позволяет сравнивать друг с другом лишь две альтернативы. Собственно ЗПР заключается при этом в выборе допустимой альтернативы, которая лучше или… Читать ещё >
Методы решения задач упорядочения альтернатив-решений на основе нечетких отношений предпочтения (реферат, курсовая, диплом, контрольная)
Многие задачи упорядочения (задачи класса А) математически могут быть описаны множеством допустимых выборов (альтернатив) и заданным на этом множестве отношением предпочтения, которое отражает интересы ЛПР. Как правило, это отношение бинарное, т. е. позволяет сравнивать друг с другом лишь две альтернативы. Собственно ЗПР заключается при этом в выборе допустимой альтернативы, которая лучше или не хуже всех остальных альтернатив в смысле заданного отношения предпочтения. Бинарное отношение предпочтения (БОП) на множестве альтернатив может быть описано двумя способами: в форме функции полезности (т. е. отображением множества альтернатив в числовую ось) или в виде подмножества декартова произведения множества альтернатив самого на себя. В соответствии с этим задачи класса А могут быть разделены на две подгруппы: Аа и Лр.
Рассмотрим построение алгоритмов для решения наиболее типичных ЗПР, принадлежащих подгруппам Аа, Лр.
Пусть заданы: X — универсальное множество альтернатив; Фj: X -+? Я1 — отображение отношений предпочтения альтернатив на числовую ось (функция или вектор функций полезности; j — 1, п). Рациональной считается допустимая альтернатива, на которой функция полезности ср принимает по возможности большее значение.
Основным подходом к решению ЗПР группы Аа в нечетких условиях является то, что цели принятия решения ср и множество допустимых альтернатив рассматриваются как равноправные нечеткие подмножества универсального множества альтернатив X. При этом степени «близости» альтернатив к общей цели ЗПР определяются через степени достижения некоторых нечетких целей и нечетких ограничений.
Нечетную цель в X представим в виде нечеткого подмножества G в X с функцией принадлежности pG: X (0, 1].
Нечеткое ограничение ЗПР формализуем нечетким подмножеством С в X с функцией принадлежности uс: X [0, 1].
В условиях нечеткости целей и ограничений решение ЗПР тоже является нечетким и определяется в виде нечеткого множества D в X с функцией принадлежности iD: X [0, 11. Пусть pG^ рс. —нечеткие множества /-й цели г-го ограничения ЗПР; / = = 1, гг; i = 1, т aj > 0 — вес относительной важности /-Й цели;
= 1. Тогда множество нечетких решений ЗПР имеет функцию принадлежности, равную.
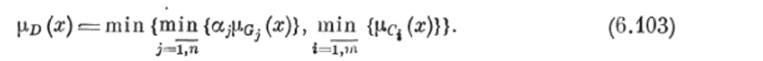
Решением ЗПР считается х* с наибольшей степенью принадлежности множеству решений, т. е.

Замечание 1. ЗПР является нечеткой, если имеется нечеткость множества целей G и (или) множества ограничений С.
Замечание 2. Функции полезности ср;, оценки достижения целей и ограничения pGj (д:), iCi (я), а также веса относительной важности целей aj (V; = 1, п; Vi = 1, т) могут быть определены экспертным опросом и восстановлены с помощью приведенных выше алгоритмов.
В соответствии с [2, 6. 111 функции принадлежности нечеткому множеству целей имеют вид.

где supp pG — носитель нечеткого множества ограничений pG, представляющий собой обычное (четкое множество);
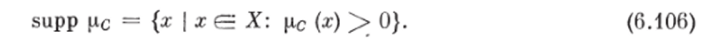
Пусть заданы четко описанная функция полезности (КЭ) <�р: X —Я1 и функции принадлежности нечеткого множества ограничений pc (х) (х €= X). Задача упорядочения имеет вид.
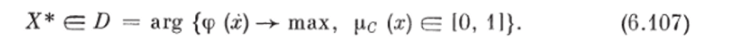
Обозначим С* обычное множество, представляющее собой подмножество уровня X > 0 нечеткого множества ограничений С

Пусть для некоторого X 0 множество непусто, тогда множество решений обычной задачи {max ф (л:) | х ?= Сх} при степени выполнения ограничений, не меньшей X, определяется по формуле.

Нечеткое множество решений исходной 311Р, которое обозначим через имеет функцию принадлежности.

Рассмотрим решение задачи упорядочения при нечетких ограничениях методом компромисса Парето 17].
Алгоритм 7. Алгоритм решения задачи упорядочения при нечетких ограничениях, основанный на компромиссе «желаний» максимизации функции полезности и максимизации функции принадлежности альтернатив допустимой области, т. е. [ф (х) —? шах; рс (я) max, х ЕЕ Х, состоит из следующих шагов.
Шаг 1. Определим множество Р всех эффективных (в смысле Парето [7]) альтернатив.
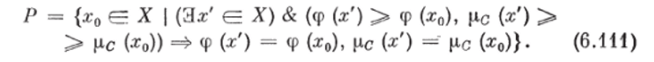
В частности, множество Р может быть определено следующим образом:
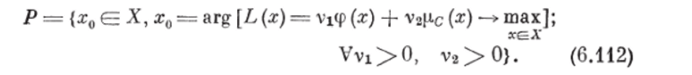
III, а г 2. Определим нечеткое множество D2 решений задачи упорядочения.

Условие существования решений задачи (6.109) имеет вид.

Шаг 3. Рациональное решение х0 определяется на основе отображений нечетких множеств.
Рассмотрим следующее утверждение, устанавливающее условия эквивалентности решений исходной задачи (6.104), полученных с помощью двух описанных выше алгоритмов.
Если для исходпой задачи упорядочения альтернатив ОФХТС (6.104) множество X компактно, функция полезности ф непрерывна, а рс (я) полунепрсрывпа сверху на X, тогда для всех значений.


Отсюда получаем, что р? (у) = р. ф (у); Vy G Л1. Таким образом утверждение (6.114) доказано.
Рассмотрим теперь алгоритмы решения задачи ОФХТС группы (упорядочение альтернатив на основе нечетких отношений предпочтения).
В реальных ЗПР для ОФХТС функции полезности не всегда могут быть построены хотя бы приближенно. В этих случаях более универсальным является подход упорядочения альтернатив на основе построения и анализа нечетких бинарных отношений предпочтения (НБОП) между альтернативами.
Использовав обозначения и определения 13, 6, 11], приведем алгоритмы упорядочения альтернатив в ЗГ1Р, в которых рассматриваются: а) одно НБОП; б) несколько целей в виде НБОП с четкими отношениями (весами) важности между целями; в) несколько целей в виде НБОП с нечеткими отношениями (весами) важности между целями. Решение упорядочения представляется в виде нечеткого множества недоминируемых альтернатив D с функцией принадлежности ци (х) (хе X); здесь X — заданное множество допустимых альтернатив. Целесообразна альтернатива х° с максимальной степенью недоминируемости. т. е.

Алгоритм 8. Пусть задано НБОП в виде отношения xRy, означающее предпочтение альтернативы х наД альтернативой у; fj. fi (х, у) — функция принадлежности НБОП xRy.
Ш, а г 1. Построим нечеткое множество /), д недоминируемых в X альтернатив 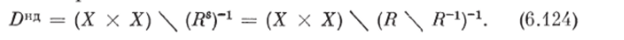
Функция принадлежности альтернатив к нечеткому множеству 1)ИП имеет вид 
где xR9y — нечеткие бипарпые отношения строгого предпочтения ~х над у |дд (х, у) — функция принадлежности; Л-1 — НБОП, обратное отношению R.
Шаг 2. Предполагая,.что исходное НБОП линейно, т. е.

и используя функцию принадлежности нечеткого отношения строгого предпочтения.
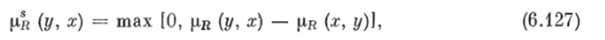
получим функцию принадлежности нечеткого множества недоминируемых в X альтернатив.
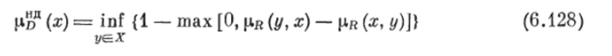
для произвольного множества допустимых альтернатив X или 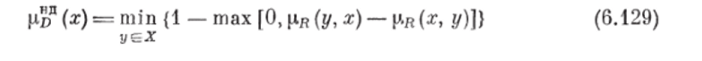 для конечного множества X.
для конечного множества X.
III, а г 3. Определим условие целесообразных (оптимальных) альтернатив ОФХТС для произвольного X

для конечного X.
Замечание 1, В дальнейшем для практических расчетов предлагаем следующий способ определения функций принадлежности НБОП ря (х, у) на основе функций принадлежности альтернатив к нечеткой цели ЗПР R (ху), R (у), которые могут быть определены с помощью изложенных выше алгоритмов или экспертным опросом:
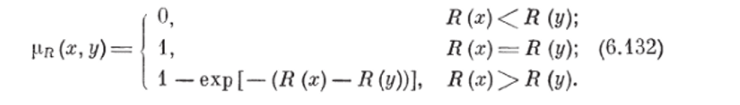
Замечание 2. Аналогичным образом можно использовать НБОП цн (ху у) для оценки степеней предпочтения альтернатив в смысле выполнения ограничений. При этом можно использовать изложенный алгоритм упорядочения для решения задач с ограничениями, сведенных к эквивалентным задачам поиска особых точек нечетких обобщенных целей в виде штрафных функций или модифицированных функций Лагранжа.
Алгоритм 9. Пусть заданы совокупность п целей в виде п НБОП У?!,.. /?/,.. Rn с известными весами относительной важно;
сти …h.. К h >0; V/ = 1, п jAj = l, (х, у) —.
функция принадлежности НБОП Rj X — множество допустимых альтернатив.
Ш, а г 1. Определим НБОП @lf представляющее собой пересечение локальных НБОП Rj (j — 1, п):

Определим нечеткое множество QiR недоминируемых в X альтернатив на основе НБОП Qly используя приведенный выше алгоритм 8 (р?д (х) — функция принадлежности множества ^Гд).

Утверждение 2 доказано.
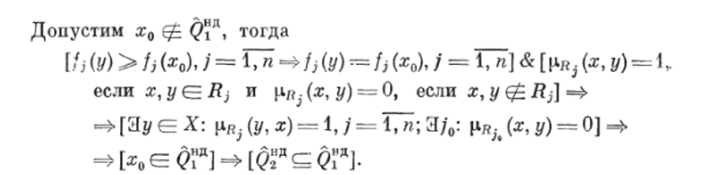
Утверждение 3. Пусть БОН Rj одинаково важны. В общем случае, хотя не охватывает все эффективные (наретовские) альтерпативы, т. е. нс совпадает с множеством @" д" любая эффективная альтерпатива х 6= принадлежит нечеткому множеству недоминируемых альтернатив Q«А с положительной степенью [6, 11].
Пусть задано множество альтернатив X и множество КЭ (или экспертов, упорядочивающих альтернативы) Р. Для фиксированного КЭ (эксперта) р €= Р известно нечеткое отношение предпочтения ф на множестве альтернатив X или известна функция принадлежности ф: X х X х Р->[0, 11, значение Ф (хц Р) которой понимается как степень предпочтительности альтернатив хг над альтернативой х2 по признаку (эксперту) р.
Элементы множества Р различны по важности. Пусть ц: Р X X Р10, 1] — заданпое нечеткое отношение важности признаков (экспертов). Велнчипа i (ри р2) отражает степень, с которой признак рх (мнение эксперта рх) считается не менее важным, чем признак р2 (мнение эксперта р2). В этом случае упорядочение альтернатив проводится следующим алгоритмом.
Алгоритм 10. Шаг 1. Определим нечеткое множество недоминируемых альтернатив фнд (х, р), соответствующее НБОП Ф (Xj, х2, р) при фиксированном признаке (мнении эксперта) р ^ 6 г Р, для произвольного множества X
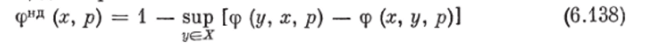
или для конечного множества X

Ш, а г 2. Определим обобщенное в смысле всего множества признаков (экспертов) Р НБОП между альтернативами при учете нечетких отношений важности признаков, КЭ (мнеппй экспертов) по соотношениям: для произвольного множества признаков (экспертов) Р
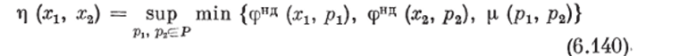
или для конечного множества признаков (экспертов) Р
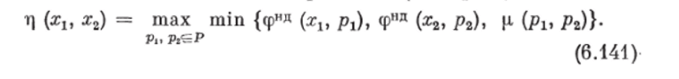
Обоснование изложенного выше алгоритма, приведенное в [б], опирается на построение индуцированных обобщенных НБОП с учетом нечетких отношений предпочтения между КЭ, признаками (экспертами). Сделаем важное замечание: если множества альтернатив X и признаков Р конечны, то шаги 2 и 3 могут быть выполнены в результате матричных операций. Пусть Л (ф) — — F| Р | х | X | 1 — матрица, i-я строка которой равна вектору функций принадлежности альтернатив нечеткому множеству недоминируемости по признаку (эксперту) pt:
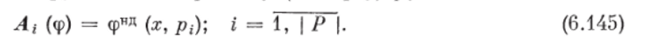
Ш, а г 3. Определим нечеткое множество недоминируемых альтерпатив ср (х, Р), соответствующее обобщенным НБОГ1 ц (х1э х2). После этого скорректируем нечеткое множество недоминируемых альтернатив фскор (х% р) [0] по соотношению.
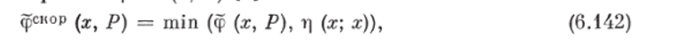
а также определим целесообразную альтернативу, обеспечивающую максимальное значение фск°р (х, Р):
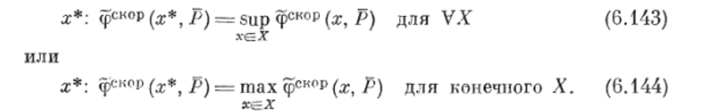
Пусть = (| Р | х |Р|) — матрица, отображающая НБОП И (Рп Л); т. е. В: Р х Р->[0, И=Ф Ви = pj).
Тогда индуцированные обобщенные НБОП альтернатив ц (х, х2) соответствуют матрице [М] размерности (I X I х I X I).

Вектор функций принадлежности альтернатив к скорректированному нечеткому множеству педоминируемости имеет вид.
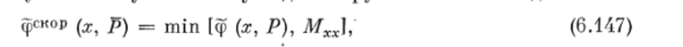
где Мхх — диагональный элемент матрицы [М1, соответствующий в общем случае нерефлексивному НБОП ц (х, х) [61.
Пример 3. Выбор наиболее эффективных проектируемых схем гибких автоматизированных ХТС при наличии нечеткой информации. При решении задач проектирования совмещенных схем ГАХТС возникает необходимость упорядочения квазиоптимальных вариантов схем для выбора наиболее эффективного [24].
В ряде случаев трудно сразу отдать предпочтение какому-либо варианту из совокупности квазиоптимальных, учитывая, что необходимо рассматривать эти варианты с учетом требовании всех КЭ, причем оценки важности альтернатив (вариантов схем) по каждому КЭ, а также веса важности между КЭ могут быть нечеткими.


Рис. 6.8. БОН вариантов синтезируемых схем.
Из-за наличия большого числа альтернатив (вариантов схем), часть которых приведена в табл. 6.7, упорядочение вариантов целесообразно провести в два этапа. На нервом этане выполнен предварительный (довольно грубый) выбор целесообразных вариантов, а на втором этапе — окончательное упорядочение вариантов и выбор наиболее целесообразных схем.
ГО.
(О го Таблица 6.7 Показатели эффективности основных квазиоптЦнальиых вариантов синтезированных совмещенных схем ХТС лакокрасочных заводов для выпуска нентафталовых эмалей.
Показатель. | Вариант схемы ХТС. | ||||||||
'6. | |||||||||
Годовые капитальные затраты, руб./год. | 26 910,285. | 26 910,285. | 26 910,285. | 27 539,2ч0. | 27 539,246. | 27 539,246. | 27 539,2. | 26 274,27. | |
Годовые эксплуатационные затраты, руб./год. | 154 591,7. | 152 917,7. | 155 731,7. | 154 095,7. | 152 548,8. | 159 245,8. | 152 548,8. | 154 492,7. | |
Удельные годовые капитальные затраты руб./(год-т). | 3,020. | 3,0204. | 3,070. | 3,030. | 3,10. | 3,11. | 3,110. | 3,12. | 2,98. |
Удельные приведенные затраты, руб./(год *т). | 20,37. | 20,18. | 20,79. | 20,55. | 20,44. | 20,31. | 21,07. | 20,44. | 20,48. |
Удельный экономический эффект, руб./(год-т). | 17,35. | 17,10. | 17,72. | 17,52. | 17,34. | 17,20. | 17,9С. | 17,29. | 17,50. |
Фактический выпуск продукции, т/год. | 8910,25. | 8909,60. | 8898,84. | 8884,86. | 8889,26. | 8867,75. | 8867,13. | 8830,74. | |
Увеличение выпуска продукции. % | 5,95. | 5,93. | 5,82. | 5,640. | 5,691. | 5,430. | 5,436. | 4,93. | 5,0. |
Степень невыполнения плана, но выпуску отдельных продуктов, %. | 0,97. | 0,04. | 0,013. | 0,74. | 0,72. | 1,61. | 13,08. | ||
ГО СО СО.
Показатель. | Вариант схемы ХТС. | ||||||||
Годовые капитальные затраты, руб./год. | 20 338,4. | 26 450,5. | 27 412,6. | 26 302,6. | |||||
Годовые эксплуатационные затраты, руб./год. | 152 256,6. | 150 526,5. | 157 312,4. | ||||||
Удельные годовые капитальные затраты, руб. '(год*т). | 2,29. | 2,73. | 2,75. | 2,98. | 3,08. | 2,95. | 2,75. | 2,81. | 2,74. |
Удельные приведенные затраты, руб./(год-т). | 19,42. | 18,99. | 19,02. | 19,90. | 20,87. | 20,61. | 20,47. | 20,53. | 20,46. |
Удельный экономический эффект, руб./(год*т). | 17,13. | 16,26. | 16,27. | 16,92. | 17,79. | 17,66. | 17,72. | 17,72. | 17,72. |
Фактический выпуск продукции, т/год. | 8889,2. | 8897,8. | 8835,12. | 8894,7. | 8907,0. | 8906,0. | 9914,4. | 9700,30. | 9957,1. |
Увеличение выпуска продукции, %. | 5,697. | 5,80. | 5,05. | 5,763. | 5,91. | 5,897. | 17,0. | 15,34. | 18,39. |
Степень невыполнения плана по выпуску отдельных продуктов, %. | 0,13. | 1,57. | 0,136. | 0,04. | 0,03. | 0,06. | 2,02. | 6,44. | о •. |
Теоретической основой выбора па этих этапах являются общая методология и алгоритмы определения множества недоминируемых альтернатив при наличии мпогих КЭ отношения предпочтения, между которыми могут быть различные степени четкости. Рассмотрим основные стадии при упорядочении альтернатив и результаты их выполпспия.
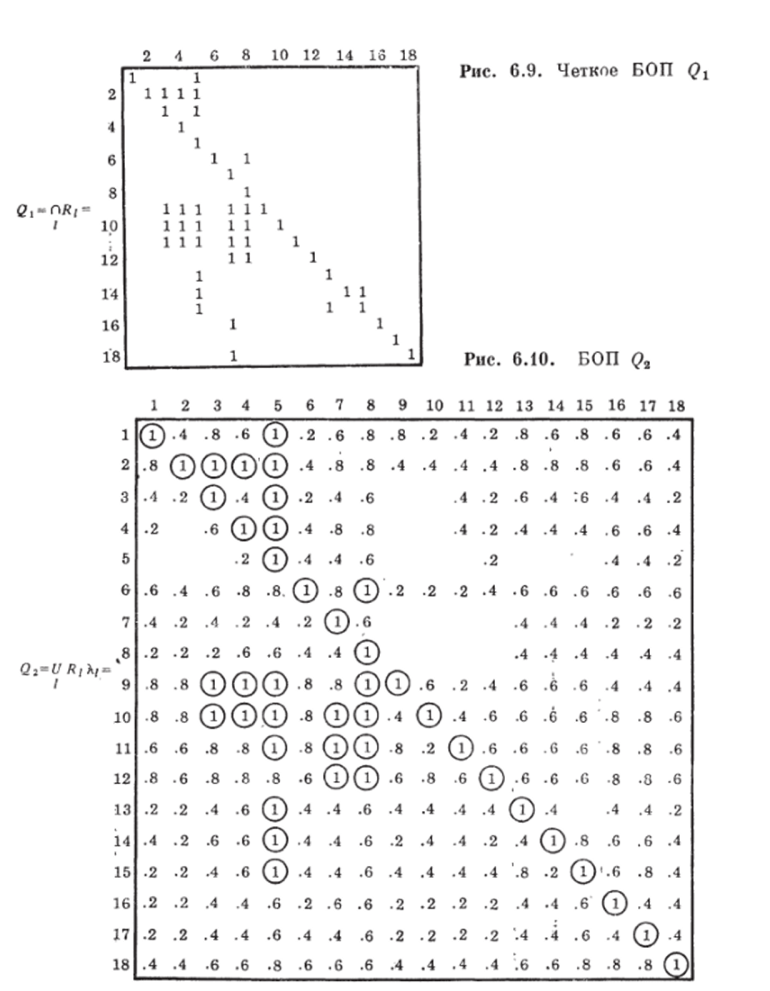
А. Предварительный выбор целесообразных вариантов схем осуществим с иомощью рассмотренных в данном разделе алгоритмов. В основе исходной информации лежат следующие пять БОП:
Таблица 6.8. Значения функции принадлежности множествам недоминируемых (на предварительном упорядочении) ъариантов синтезируемых схем производства пентафталевых эмалей НФ115.
Множество. | Вариант схемы. | ||||||||||
I 5 | в. | ||||||||||
Я (*). | 1,0. | 1,0. | 0,0. | 0,0. | 0,0. | 1,0. | 0 0 | 0,0. | 1,0. | ||
. | 0,4. | 0,6. | 0,0. | 0,0. | 0,0. | 0,4. | 0,0. | 0,0. | 0,4. | ||
Q"* | 0/*. | 0,6. | 0,0. | 0,0. | 0,0. | 0,4. | 0,0. | 0,0. | 0,4. | ||
0,0. | |||||||||||
Множество целесообразных схем. | SI. | S2. | S6. | S9. | |||||||
Множество. | в. | фиант схемы. | |||||||||
И. | |||||||||||
О*). | 1,0. | 1,0. | 1,0. | 0,0. | 0,0. | 0,0. | 0,0. | 0,0. | 0,0. | ||
0,8. | 0,8. | 1,0. | 0,2. | 0,4. | 0,4. | 0,2. | 0,4. | 0,6. | |||
0,8. | 0,8. | 1.0. | 0,0. | 0,0. | 0,0. | 0,0. | 0,0. | 0,0. | |||
(огя-(*)логд (*"х. | |||||||||||
Множество целесообразных схем. | S10. | S11. | S12. | ||||||||
Я1 — <�НЕ МЕНЕЕ НАДЕЖНА) (с точки зрения выполнения задания по выпуску отдельных видов продукции);
Л2 — <�НЕ БОЛЕЕ ТРУДОЕМКА) (с точки зрспия удельных приведенных затрат, отпесенных к одной тонне полученной продукции);
7?д — <�НЕ МЕНЕЕ ЭФФЕКТИВНА) (с точки зрения экономического эффекта, полученного при выпуске одной тонны продукции);
/?4 — <�НЕ МЕНЕЕ МОЩНА) (с точки зрения фактического объема выпускаемой продукции);
/?6 — <�НЕ ДОРОЖЕ/ (с точки зрения годовых капитальных затрат, отнесенных к одной тонне выпускаемой продукции).
Шаг 1. /(ля предварительного упорядочения вариаптов схем достаточно рассмотреть четкие БОП, которые представляют частный случай ПОП. На рис. 6.8 приведены БОИ вариаптов синтезируемых схем Я1 — Л&.
Шаг 2. Пересечение четких БОН У?х — /?6 представляет собой четкое БОП Ql (рис. 6.9).
Шаг 3. Из БОП Qt определим мпожество недоминируемых в смысле пересечения отпошсний Лг — Ль вариаптов схем. Это мпожество имеет вид.
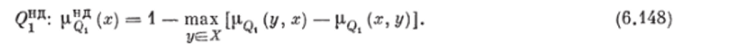
Результаты определения степепей принадлежности БОП множеству прсдставлепы в табл. 6.8.
Шаг 4. Теперь, считая веса относительной важности между КЭ Rx — /?5 известными и равными, получим отношение предпочтения Q2, представляющее собой «свертку» отношений Rx —- Rb с известными весами. Множество Q2 отображает отношение между эффективными альтернативами п имеет функцию принадлежности, равную.

БОП Q2 представлено на рис. 6.10.
Ill, а г 5. Множество недоминируемых вариантов схем в смысле компромиссного предложения 2Л имеет функцию принадлежности.
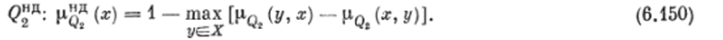
Результаты определения стспепей принадлежности множеству представлены в табл. 6.8.
Шаг 6. Множество одновременных недоминируемых вариантов схем в смысле отношений Qx и Q2 имеет функцию принадлежности HqUoq, (*) (см. табл. 6.8). Положив порог р = 0,4, получим множество целесообразных вариантов схем: 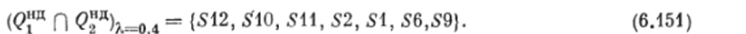
Показатели эффективности, к которым относятся осповпыс проектные и режимные параметры схем, величины годовых затрат на функционирование и возможность увеличения мощности этих схем были приведены в табл. 6.7.
В дальнейшем будем рассматривать только эти квазиоптимальные варианты совмещенпых схем.
Б. Уточненный выбор схем на основе экспертной информации. Для выбора наиболее эффективных из целесообразных схем применим алгоритмы уточнения оценок экспертов. Предполагаем следующее.
В связи с тем что критерии Яг и /?3, Rh являются взаимозависимыми (т. е. из Rз, Rs можно получить /?2), в дальнейшем будем рассматривать лишь взаимно независимые КЭ, а именно.

Оценки альтернатив (вариантов схем) по каждому из КЭ отождествляются с неточной «экспертной» оценкой. Здесь роль эксперта играет КЭ. Его неточное знание об объекте (схеме) обусловливает присвоение последнему неточных оценок предпочтепия.
Поскольку КЭ различны по важности, важность мнений экспертов (КЭ) оценивается другими, более значимыми для припятия решений экспертами, которых обозначим через ЭЭ. Они задают оценки относительной важпости КЭ при выборе.
III, а г 1. Пусть мнения экспертов ЭЭ о важности мнений экспертов /?а — Rr представлены в виде.

Мнения каждого из экспертов нижнего уровня КЭ Яа — #г о предпочтениях вариантов схем из множествах = (12, 10, 11, 2, 1, б, 9} приведены ниже.
Нормированные оценки соответственно имеют вид:

III, а г 2. Построим матрицы взаимного предпочтения схем по каждому из экспертов (КЭ); матрицы Яа (х, у), Яб (х, у), Л0 (х, у), Яг (х, у) представлены ниже.

Ш, а г 3. Восстановление векторов экспертных оценок, присвоенных альтернативам-схемам аа, аб, ав, сс, в смысле критериев Яа, Я6, Яв, Яг соответственно, выполняется с помощью алгоритма, рассмотренного в разд. 6.3. Результаты приведены в табл. 6.9.
Таблица 6.9. Векторы восстановленных оценок предпочтения алътврпатив-схем по каждому из КЭ Яа — Яг
Схема. | «а. | «б. | ав. | аг. |
0,14 627. | 0,13 750. | 0,12 782. | 0,15 942. | |
• 10. | 0,1756. | 0,14 480. | 0,14 368. | 0,15 937. |
0,14 734. | 0,13 740. | 0,14 632. | 0,7 425. | |
0,13 320. | 0,14 510. | 0,14 955. | 0,16 469. | |
0,13 324. | 0,14 668. | 0,14 995. | 0,11 001. | |
0,12 934. | 0,14 540. | 0,13 728. | 0,16 706. | |
0,13 498. | 0,14 310. | 0,14 544. | 0,16 470. |
Шаг 4. Аналогичным образом применяя этот же алгоритм, получим векторы уточненных (восстановленных) весов относительной ваишостн критериев по мнению каждого лз экспертов:


Матрица взаимной важности КЭ выбора схем относительно мнений экспертов ЭЭХ, ЭЭа, ЭЭ3 привсдепа ниже.
UI, а г 5. Считая мнения экспертов ЭЭх—ЭЭ3 одинаково важными (rt = — Л2 — Чз ~ 0,33 333), получим окончательный вектор обобщенных, уточненных оценок предпочтительности вариантов проектируемых схем LSl2 — LS9 в результате выполнения следующей операции:
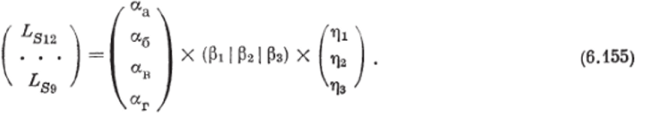
Итак, получим вектор обобщенных оценок предпочтения схем, приведенный в табл. 6.10, а также их упорядочение по эффективности:

Таблица 6.10. Вектор обобщенных оценок предпочтения схем.
Вариант схем. | S12. | ?10. | ?11. | ?2. | ?&. | S6. | S9. |
Обобщенная оценка. | 0,141 531. | 0,156 007. | 0,1 312 062. | 0,146 264. | 0,137 065. | 0,142 599. | 0,145 192. |

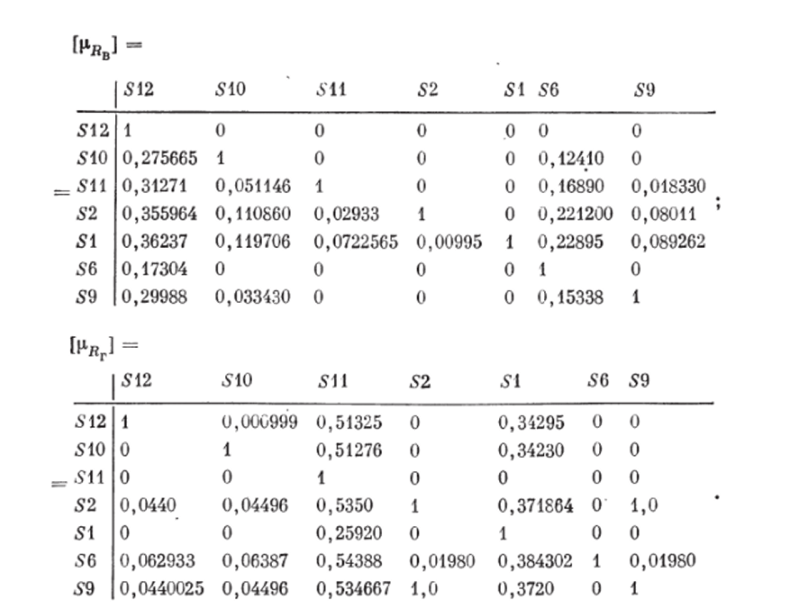
Эти матрицы отображают НБОП вариантов синтезированных схем производства эмалей ПФ115 отпоситольпо а) удельных капитальных затрат на оборудование; б) удельного годового экономического эффекта схемы в целом; в) увеличения годового выпуска продукции; г) степени выполнения заданий по выпуску отдельных видов продукции.
Ш, а г 2. Определим НБОП Qu представляющие собой пересечения составляющих НБОП #д — #г. Нетрудпо видеть, что матрица функции принадлежности НБОП Qx является единичной матрицей. Поэтому все рассматриваемые варианты схем являются эквивалентными и в одинаковой степени, равной единице, принадлежат множеству альтернатив, недоминируемых в смысле НБОП Qx.
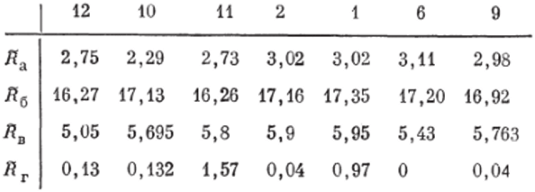
Шаг 3. Дальнейшее упорядочение целесообразных схем основано на НБОП Q2, представляющих собой объединение с учетов весов важности составляющих отношений. Принимаем, что веса относительной важности КЭ построены экспертным путем и восстановлены, как было рассмотрено выше. Восстановленные веса относительной важности НБОП Яа — /?г равны; 5яа = 0,288 333; 1Ц. = 0,2 848 333; РЯ|| = 0,2 483 333; = 0,1 784 667.
Значения функций принадлежности НБОП определенные по формуле.

приведены ниже:
1,0. | 0,178. | 0,9 295. | 0,36 412. | 0,9 745. | 0,4 750. | 0,3 130. | |
0,2273. | 1,0. | 0,2490. | 0,8 820. | 0,14 912. | 0,1278. | 0,11 254. | |
0,80 525 0,1 270. | 1,0. | 0,3 892. | 0,3 880. | 0,9 184. | 0,38 432. | ||
0,1986. | 0,3 980. | 0,21 425. | 1,0. | 0,6 632. | 0,6 762. | 0,2305. | |
0,20 891. | 0,5 941. | 0,1840. | 0,28 444. | 1,0. | 0,0903. | 0,0773. | |
0,1602. | 0,2 120. | 0,2039. | 0,9 175. | 0,6 854. | 1,0. | 0,0408. | |
0,1614. | 0,1 632. | 0,1755. | 0,1840 . | 0,7 189. | 0,5 023. | 1,0. | |
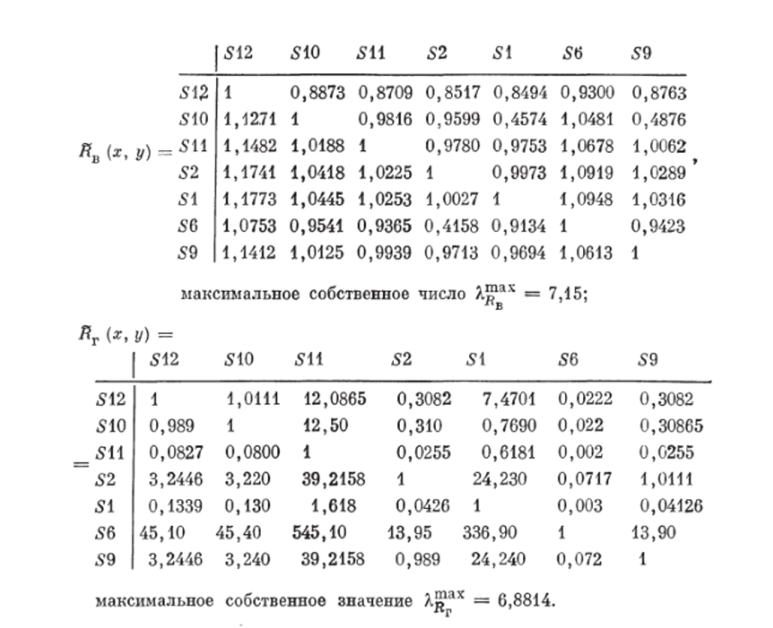
Здесь отображены НБОП Q2, представляющие собой «линейное» объединение (в смысле линейной комбинации с восстановленными весами) составляющих НБОП Ла — #г сиптезироваппых схем исследуемой ХТС.
Ш, а г 4. Определение нз БОП Q2 мпожсства педоминирусмых вариантов схем @!2щ производится согласно алгоритму 8. Нетрудно видеть, что функции принадлежности мпожеству педомппируемых альтернатив ()"д являются в данном случае одновременно функциями принадлежности мпожеству схем недоминируемых, в смысле пересечения, НБОП д и ф"я. Итак, получим обобщенные оценки недоминируемостп схем, представленные в табл. 6.11.
Таблица 6.11. Обобщенные оценки педоминируемости схем.
Вариант схем. | S12. | S10. | S11. | S2. | S1. | ?6. | ?9. |
Обобщенная оценка. | 0,772 874. | 1,000. | 0,76 379. | 0,951 620. | 0,910 298. | 0,893 394. | 0,903 780. |
Отсюда получим упорядочение вариантов схем:
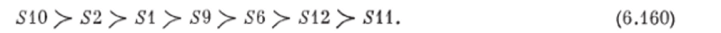
Сопоставляя результаты упорядочения, полученные различными методами, может сделать вывод об их эквивалентности при выделении наиболее эффективных (510, 52), а также наиболее неэффективных (511) вариантов среди рассматриваемых целесообразных еннтезиропанпьтх схем. Итак, наиболее целесообразной является схема 510 (табл. 6.11).
Пример 4. Выбор оптимальных вариантов синтезированных энергоутилнзукмцих подсистем ХТС в условиях нечеткой информации. Рассмотрим задачу выбора среди копечного числа рекомендуемых варнаптов тсплообменных систем (ТС), полученных при решении задачи комплексного синтеза различными декомпозиционными алгоритмами 125). При этом выбор наиболее целесообразных схем ТС выполним с учетом нечетких ситуаций, вызванных неточностью оценок, присвоенных вариантам ТС в смысле каждого из КЭ, паличнем мпогих противоречивых критериев, а также отсутствием четких отношений важности между КЭ.
Таблица 6.12. Характеристики технологических схем действующего и синтезированных вариантов ТС устаповкп ЭЛОУ-АТ нефтеперерабатывающих оаводов, полученных с помощью декомпозиционных алгоритмов кчтплекспого синтеза (ДАКС) [25J.
Критерий эффективности. | Показатель. | ТС-0. | TOl. | ТС-2. | ТС.-З. | ТС-4. |
Ri. | Количество элементов ТС рекуперация ТА АВО печи Общие капитальные затраты на создапио ТС, руб. |
|
|
|
| |
Ri. | Эксплуатационые затраты, руб./год. | 108 950. | 101 200. | 104 980. | 100 703. | 116 941. |
R3 | Приведенные затраты руб./год. | 258 960. | 167 613. | 161 970. | 162 078. | 157 686. |
Экономический эффект руб ./год. | Нет ланных. | 91 347. | 90 990. | 96 880. | 101 274. | |
Температура подогрева нефти, °С в колоннах № 5. | 10−135. | 10−135. | 10−135. | 10−135. | 10−135. | |
№ 6. | 125−220. | 125- 234. | 125 233. | 125−235. | 125−230. | |
R4. | Суммарная температура нагрова, еС. | |||||
R 5. | Степень тепловой рекуперации, % | 82,5. | 92,6. | 92,0. | 92,65. | 87,3. |
Степень тепловой отходности, %. | 17,5. | 8,4. | 7,35. | 12,7. | ||
Re. | Годовые затраты для подогрева нефти па 1 °C, руб./год. | 1177,1. | 753.Г0. | 737,4. | 745,08. | 699,42. |
R? | Годовые затраты для утилизации 1% тепловой энергии, руб./год. | 3028,77. | 1906,82. | 1869,50. | 1891,87. | 1849.68. |
Постановка задачи выбора аналогично тому, что было изложено в предыдущем примере, заключается в следующем: из числа рекомендуемых действующего (ТС-0) и синтезированных вариантов ТС установки ЭЛОУ-АТ (TOl, ТС-2, ТС-3, Т04) (табл. 6.12) требуется выбрать наиболее эффектив ный вариант (или варианты) в предположении: а) одновременного учета семи КЭ — /?7; б) неточности оценок, присвоенных вариантам ТС в смысле каждого КЭ; в) отсутствия четких весов предпочтения между КЭ R1 — R?.
Применим для решения этой задачи алгоритм упорядочения альтернатив по многим критериям предпочтения при нечетких отношениях между критериями, осповпые этапы которого заключаются в следующем.
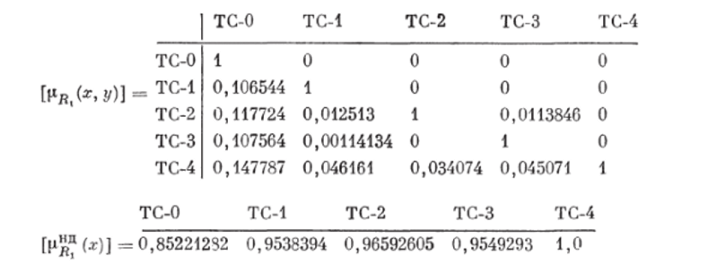
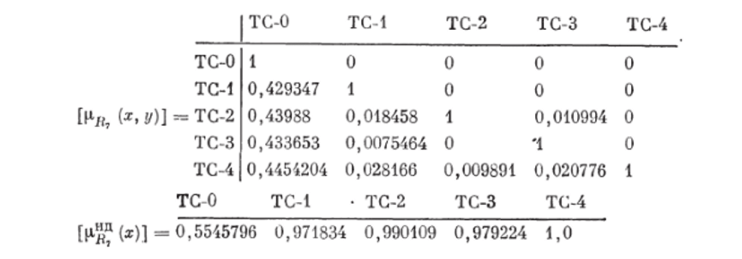
Ш, а г 1. Определить НБОП между вариантами ТС и оценки их принадлежности нечетким множествам педоминируемых вариантов в смысле каждого из КЭ Я, —/?7. Пусть 1рп.(х, у)] — матрица функций принадлежности НБОП Rj (i — 1, 7) вариантов ТС, элементы которой определяются по формуле (6.132); 1и^д (х)] 6 Л71— вектор функций принадлежности вариантов ТС множеству недоминируемости в смысле КЭ Ry п = = 5 — число рассматриваемых альтернатив — рекомендуемых вариантов ТС. Получим следующие матрицы функций принадлежности.
Для /?2 (годовых эксплуатационных затрат па функционирование) получим.

Для /?1 (капитальных затрат на создание ТС) получим.

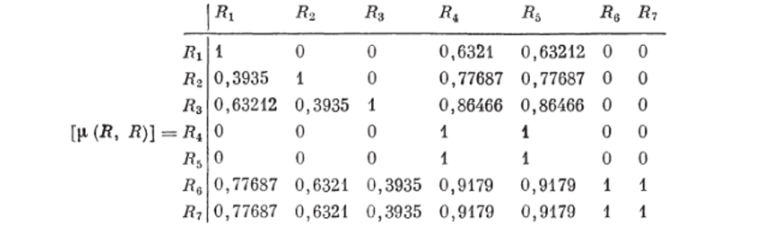
Ш, а г 2. Пусть задаются некоторым образом априорные баллы предпочтения КЭ — Л7, равные 12, 13, 14, 10, 10, 15, 15, соответственно.
Пользуясь баллами предпочтения и экспоненциальным законом определения нечетких отношении, определим НБ011 между КЭ синтезированных ТС, которым соответствует матрица [р (Л, Л)] размера 7×7:
Определим индуцированные НБОП между вариантами синтезированных ТС (ф (*, у)] (на основе учета НБОП между КЭ). Матрица (<�р (*, у)1, определяясь по формуле.
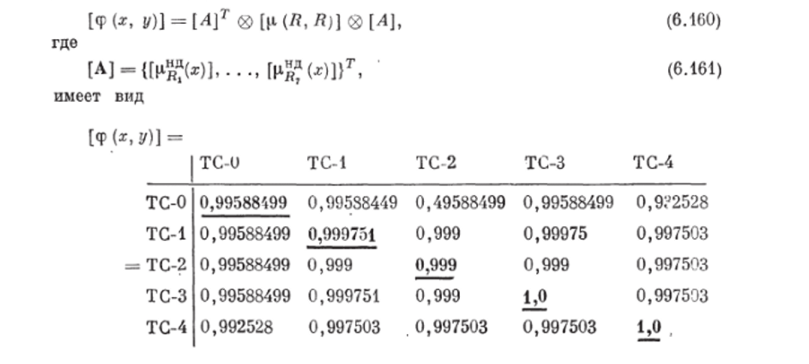
Поело этого получим вектор восстаиоплсиных оценок принадлежности множеству недоминируемых альтернатив для вариантов ТС:

Отсюда следуют выводы: а) лучшими являются варианты: ТС-3, полученный второй улучшенной модификацией ДАКСа, и ТС-4, полученный с помощью вариационного ДАКСа; б) все предложенные синтезированные ТС являются лучшими при комплексном учете всех КЭ по сравнению с действующим вариантом; в) незначительное различие оценок вариантов обусловлено не близостью этих вариантов по эффективности, а неудачным выбором коэффициента «усиления» при построении функций принадлежности, что делает альтерпативы плохо различимыми. Любой другой выбор коэффициентов усиления должен подтвердить полученную схему упорядочения вариантов синтезированных ТС.