Метод релаксации.
Численные методы.
Основы научных вычислений

Теперь мы имеем итерационную матрицу, которая зависит от параметра со. Можно подобрать такое значение параметра со, которое обеспечивает минимальное значение s (B|R (co)). Такое значение называется оптимальным значением параметра релаксации и обозначается со ()|)1. Метод релаксации (3.24) основывается на методе Якоби (BjR (l) = Bj) и i (BJR (co)) = 1 + со (ЦВ|) — 1). ПустьХ/< А.(В|) < Хг, тогда… Читать ещё >
Метод релаксации. Численные методы. Основы научных вычислений (реферат, курсовая, диплом, контрольная)
Основной вопрос, возникающий при использовании итерационных методов: как достичь наиболее быстрой сходимости, или, другими словами, как построить итерационную матрицу для данной системы, которая имела бы наименьший спектральный радиус s (В). Для этого необходимо иметь некоторый способ управления свойствами итерационной матрицы В. Один из таких способов реализуется в методе релаксации.
Сначала обсудим общую схему этого метода. Рассмотрим систему (3.1) с SPD матрицей А. Для вектора приближенного решения х^ мы определим функционал ошибки в виде.
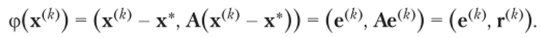
Для того чтобы вычислить другой вектор х^к+1 который отличается от только п-й компонентой и такой, что ср (х(А'" 1)) < ф (х(А,)), положим х(А'+1) = x(Af) + ab" (Ь" — базисный вектор, см. 3.1). Тогда легко получить, что где.
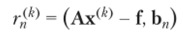
— п-я компонента вектора невязки. Сумма второго и третьего слагаемых в (3.23) принимает отрицательное значение, если выбрать параметр так, чтобы.
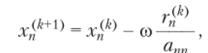
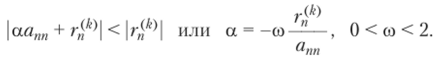
Тогда п-я компонента вектора х(/'+1^ вычисляется как.

где со называется параметром релаксации. Выбирая таким же образом параметр, а для п = 1,…, N, мы получим следующую итерационную схему:
Эквивалентная форма (3.12) для этой итерационной схемы может быть также записана в виде.
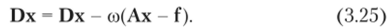
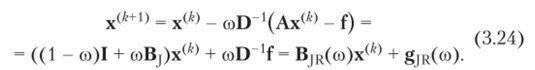
Теперь мы имеем итерационную матрицу, которая зависит от параметра со. Можно подобрать такое значение параметра со, которое обеспечивает минимальное значение s (B|R(co)). Такое значение называется оптимальным значением параметра релаксации и обозначается со()|)1. Метод релаксации (3.24) основывается на методе Якоби (BjR(l) = Bj) и i (BJR(co)) = 1 + со (ЦВ|) — 1). ПустьХ/< А.(В|) < Хг, тогда оптимальное значение параметра релаксации вычисляется как.
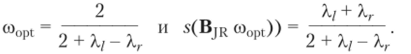
Пример 3.4 (оптимальный параметр релаксации для итерационной схемы (3.24)).
Рассмотрим следующую матрицу для системы (3.1):
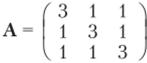
Собственные значения матрицы Якоби Вр -2/3, 1/3, 1/3 и, следовательно, .s (Bj) = 2/3. Учитывая, что Х/ = 2/3 и Х, = 1/3, получим coopt ~ 0.8571. Тогда s (BjR(coopt)) ~ 0.4286 < s (Bj), и это говорит о том, что можно ускорить сходимость по сравнению с методом Якоби.
Следующий логический шаг — построить метод релаксации, основанный на методе Гаусса — Зейделя (3.21). Учитывая выражение (3.18), можно преобразовать (3.25) в следующую эквивалентную систему: 
Как и прежде, обращать матрицу D + ooL не нужно, а записать итерационную схему в виде 
Матрица D + coL — нижняя треугольная, и система (3.26) может быть легко решена относительно вектора х(А+, На практике было замечено (в некоторых случаях доказано), что итерационная схема (3.26) сходится медленнее при со 1 (верхняя релаксация). Поэтому обычно используется со = 1, и за итерационной схемой (3.26) закрепилось название метод последовательной верхней релаксации (SOR, Successive Over-Relaxation). Для небольшого числа специфических (но важных) задач оптимальное значение параметра релаксации может быть определено. Рассмотрим кратко этот случай.
Матрица Якоби Bj = I — D 'A = -D fL — D 'U называется согласованно упорядоченной, если.
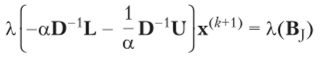
для любого параметра, а ^ 0. Например, блочно-трехдиагональные матрицы вида.

где Dm — квадратная матрица размером NmxNm (т = 1, …, р); Lm и U/w_! — матрицы размером NmxNm+i и j XNm соответственно (т = 2, Nj + … + Л^= N) являются согласованно упорядоченными. Пусть, А — SPD согласованно упорядоченная матрица. Если метод Якоби для этой системы сходится (s (Bj) < 1), то значение оптимального параметра релаксации для метода SOR вычисляется по формуле 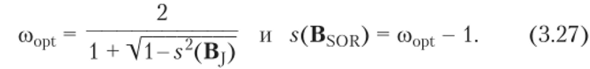
Пример 3.5 (метод SOR).
Рассмотрим снова систему (3.20) из примера 3.2. Матрица, А трехдиагональная (это специальный случай блочно-трехдиагональной матрицы) и, следовательно, согласованно упорядоченная. В дополнение, она также является SPD матрицей, и мы можем вычислить соор1 согласно выражению (3.27). Для данной матрицы s (Bj) = 0.5V2, тогда coopt ~ 1.17 157 и s (Bs ()R) ~ ~ 0.17 157. Это означает, что для данной системы метод SOR обеспечивает очень быструю сходимость по сравнению с методами, рассмотренными выше. Результаты вычислений для начального вектора х(0^ = (0, 0, 0)г и s/; = 10 5 представлены в табл. 3.3.
Таблица 33
k | х. | X. х_. N5. | ||е||2 |
| 7.5798е-01. | 5.7109е—01. | |
| 4.4975е-01. | 1.2202е-01. | |
| 7.9500е-06. | 1.5046е-06. |
Как показывают эти результаты, требуется только 9 итераций, для того чтобы получить приближенное решение с заданной точностью, и это в два раза меньше по сравнению с методом Гаусса — Зейделя.
Вычисление спектрального радиуса матрицы Якоби часто требует значительных вычислительных затрат, поэтому иногда прибегают к грубой оценке s (Bj), что позволяет нолучить приемлемое значение параметра релаксации, близкое к coopt.
Что касается других типов матриц, то простые способы вычисления значения оптимального параметра релаксации не известны. Однако известны достаточные условия, при которых метод SOR сходится:
1) если, А — SPD матрица, то метод SOR сходится при О < со <2. В этом случае значение параметра релаксации, определяемого по формуле (3.27), близко к оптимальному, так как юор1 — 1 < s (BSOR) < Vcoopt — 1;
2) если, А — матрица со строгим диагональным преобладанием или неразложимая матрица со слабым диагональным преобладанием, то существует такое со* > 1, что метод SOR сходится при 0 < со < со*.