Регистрация и восстановление волновых оптических полей в пространстве

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРЕОБРАЗОВАНИЯ ВОЛНОВЫХ ОПТИЧЕСКИХ ПОЛЕЙ В СВОБОДНОМ ПРОСТРАНСТВЕ

Изображения в когерентно-оптических системах формируются на основе различных физических принципов преобразования волновых полей. Так, в классической оптике изображение формируется с помощью оптических устройств, состоящих из набора линз и зеркал, в радиоастрономии для этого требуются специальные антенны и чувствительные квантовые приемники, акустические поля могут регистрироваться с помощью матрицы микрофонов.

На рис. 1.1 показана типичная система образования оптических изображений.

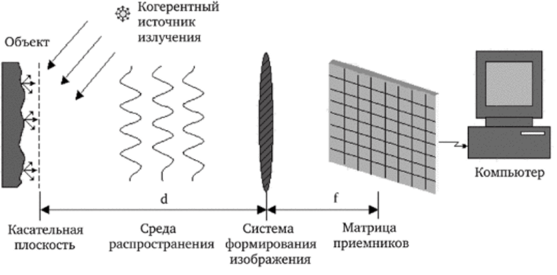
Рис. 1.1. Схема формирования изображений на фотоприемнике.

Рассмотрим математическую модель преобразования волновых полей в оптических системах. Необходимо определить комплексное поле в какой-либо плоскости, зная его значения на поверхности объекта. Это представляет собой достаточно сложную задачу. Чтобы ее не усложнять, ограничимся несамосветящимися прозрачными объектами и монохроматическим освещением. Свойства объекта, определяющие его способность отражать и рассеивать падающее на него излучение, описываются коэффициентом отражения излучения по интенсивности Ь (х, у) или комплексной амплитуде b (x, y, z) — функции координат на поверхности объекта. Коэффициент отражения по амплитуде — комплексная функция, которая может быть представлена в виде.

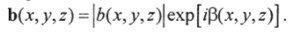
Ее модуль |/>| и фаза р показывают, во сколько раз изменяются амплитуда и фаза излучения в точке (х, у, г) поверхности объекта после отражения (здесь фаза — угол отражения).

Функции b и Ь связаны соотношением.

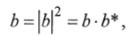
где * - знак комплексного сопряжения. Зная функцию b (x, y, z), уравнение поверхности тела F (x, у, z) = 0 и распределение амплитуды и фазы падающего на объект света, можно в принципе вычислить распределение амплитуды и фазы рассеянного света в произвольной точке пространства.

Пусть A (x, y, z) cxp'^al-^X'^y— распределение амплитуды и фазы освещения на поверхности объекта. Тогда поле на некоторой поверхности наблюдения можно описать с помощью интегрального соотношения Кирхгофа [1].

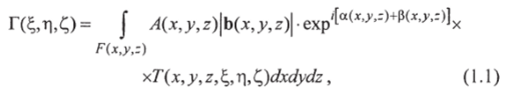
где интегрирование производится на поверхности объекта F (x, у, г). Вид ядра этого преобразования Т (х, у, г, ?, т|, Q зависит от пространственного расположения объекта и поверхности наблюдения. Это преобразование обратимо: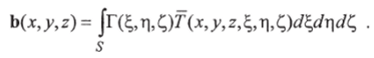

Здесь Т — оператор, взаимный Г, а интегрирование производится по поверхности наблюдения S. Это выражение описывает процесс восстановления волнового поля.

Функцию Г (?, г|, Q можно назвать математической голограммой. Задача синтеза голограмм заключается в вычислении Щ, л, Q по заданной функции Ь (дг, у, г) и ее регистрации в форме, которая бы допускала взаимодействие с излучением для визуализации и восстановления b (.v, y, z). Вычислить интеграл (1.1) в общем случае удастся только для очень простых объектов, заданных небольшим количеством отдельных линий или точек. В общем случае приходится прибегать к различного рода упрощениям [2]. Упрощение, к которому можно прибегнуть без большого ущерба, состоит в сведении трехмерной задачи к двумерной. Для этого поверхность наблюдения считается плоской, а распределение амплитуды и фазы волны на поверхности объекта заменяется согласно законам геометрической оптики распределением амплитуды и фазы на плоскости, касающейся объекта или достаточно близкой к нему (чтобы при пересчете амплитуды и фазы пренебречь дифракцией и пользоваться законами геометрической оптики), и параллельной плоскости наблюдения. В этом случае (1.1) запишется в виде.

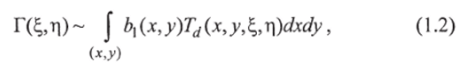
где Ь (х, у) — комплексная функция, полученная в результате пересчета амплитуды и фазы поля, отраженного объектом, на плоскость (д;, у), касательную к нему и параллельную плоскости наблюдения; d — расстояние между двумя плоскостями (.х, у) и (^, л) (рис. 1.2).

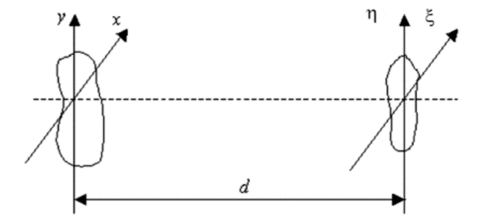
Рис. 1.2. Плоскости пересчета амплитуды и фазы.

Очевидно, если угол, под которым виден объект с поверхности наблюдения (угол охвата), и площадь наблюдения малы, то это естественная аппроксимация. Задачи, где угол охвата велик, необходимо свести к задаче расчета при малом угле охвата. При этом для реализации больших углов охвата поверхность наблюдения можно разбить на небольшие фрагменты, аппроксимируемые плоскостями, и рассматривать голограммы для отдельных фрагментов, каждая из которых представляет часть общего угла и воспроизводит объект в своем ракурсе.

Ядро преобразования (1.2), связывающее распределение света на двух параллельных плоскостях, имеет вид.

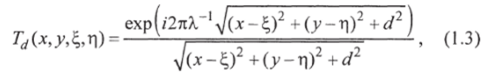
где X — длина волны излучения.

Если геометрические параметры тела малы по сравнению с расстоянием d до плоскости наблюдения, это вместе с условием малости площади наблюдения приводит к следующему допущению:

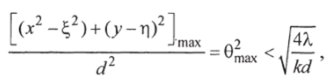
ГДС Ощах максимальный угол (в радианах), под которым наблюдают объект с расстояния d; к — коэффициент допустимой фазовой ошибки, равной я/4, в передаче аргумента экспоненты в (13).

Тогда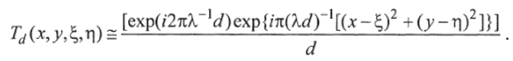

В этом случае (1.2) переходит в интеграл Френеля:

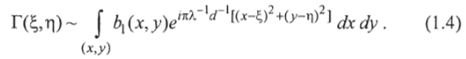
Преобразование, описываемое этим соотношением, называется преобразованием Френеля.

Далее, если 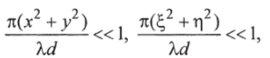то этими составляющими в (1.4) можно пренебречь. В этом случае интеграл Френеля (1.4) переходит в интеграл Фурье

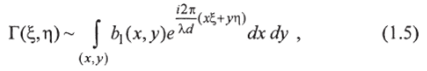
который соответствует дальней зоне дифракции (дифракции Фраунгофера).

Таким образом, при прохождении оптического волнового фронта через свободное пространство на некотором расстоянии происходит преобразование Френеля, которое далее, при увеличении расстояния, переходит в преобразование Фурье (рис. 1.3).

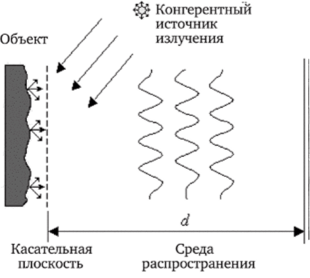
Рис. 1.3. Преобразование оптического волнового фронта в свободном пространстве.

Для пересчета комплексного поля на поверхности объекта в комплексное поле в какой-либо другой плоскости были приняты следующие допущения.

• 1. Ограничимся несамосветящимися непрозрачными объектами и монохроматическим освещением.
• 2. Сведем трехмерную задачу к двумерной. Поверхность наблюдения считаем плоской, а распределение комплексного поля на поверхности объекта заменяем в соответствии с законом геометрической оптики распределением поля на плоскости, касающейся объекта или достаточно близкой к нему (чтобы при пересчете пренебречь дифракцией и пользоваться геометрической оптикой) и параллельной плоскости наблюдения.
• 3. Допустим, что геометрические размеры тела малы по сравнению с расстоянием R до плоскости наблюдения.
• 4а. Если 0_тах — максимальный угол (в радианах), под которым наблюдается объект с расстояния d, такой, что

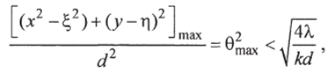
где к — коэффициент допустимой фазовой ошибки, равной л/4, то такая область называется областью Френеля, а поле в этой области записывается в виде преобразования Френеля от исходного поля в плоскости объекта (1.4).

46. Если 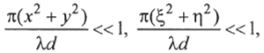то это область Фраунгофера. Преобразование записывается в виде интеграла Фурье (1.5).

Преобразование Френеля в вычислительном отношении удобнее выразить через интегральное преобразование Фурье.

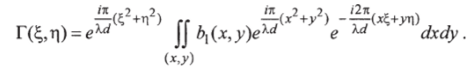
Преобразование Фраунгофера представляет собой с точностью до множителей пространственный фурье-спектр функции Ь (х, у):

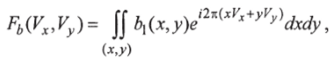
взятый по координатам V_x, V_y в масштабе (рис. 1.4).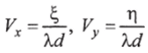

Тогда (1.5) можно представить в виде.

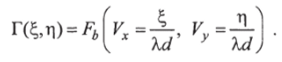
Прохождение оптического волнового фронта через свободное проегранегво можно описать преобразованием Френеля, которое с увеличением расстояния переходит в преобразование Фурье. Чтобы определить комплексную амплитуду исходного волнового фронта.

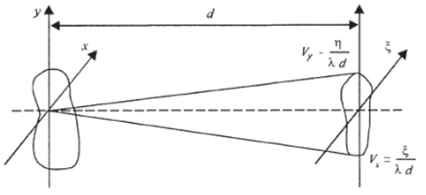
Рис. 1.4. Пространственные частоты.

на поверхности объекта, необходимо обратное преобразование. Для этого в плоскость г) следует поместить линзу (рис. 1.5).

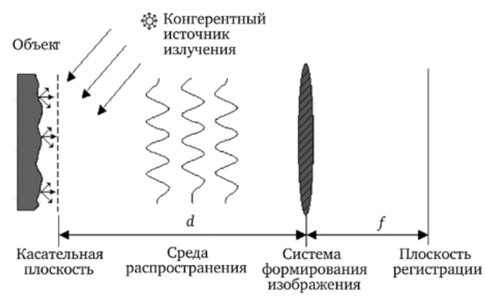
Рис. 1.5. Формирование изображения.

Рассмотрим простейшую оптическую схему (рис. 1.6). На линзу падает распространяющаяся в направлении z плоская волна с комплексной амплитудой непосредственно вблизи линзы а/.

Выражение для комплексной амплитуды в плоскости у₂ будет иметь вид, похожий на соотношение (1.5):

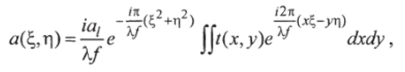
где t (x, у) — комплексная амплитуда пропускания плоского транспаранта, расположенного сразу за линзой; Я/ - апертура линзы.

Если на тонкую линзу с примыкающим к ней транспарантом падает плоская волна, то распределение комплексных амплитуд в задней фокальной плоскости линзы пропорционально произведению фазового множителя сферической волны и фурье-образа пропускания транспаранта.

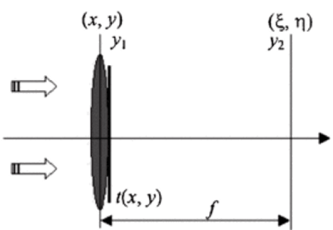
Рис. 1.6. Преобразование, осуществляемое тонкой линзой.

Фотоприемники регистрируют интенсивность.

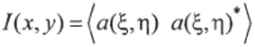
(угловые скобки означают осреднение).

При этом фазовый множитель сокращается, поскольку.

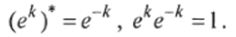
При распространении волнового поля, отраженного от диффузного объекта, на некотором расстоянии d происходит преобразование Френеля комплексной амплитуды, которое с увеличением расстояния переходит в преобразование Фурье.

Для получения значений комплексной амплитуды исходного волнового фронта необходимо сделать обратное преобразование. С этой целью в плоскость (?, г|) следует поместить линзу (рис. 1.7). В плоскости (дГ|, д/|) с точностью до постоянных множителей распределение интенсивности совпадет с ее распределением на плоскости объекта.

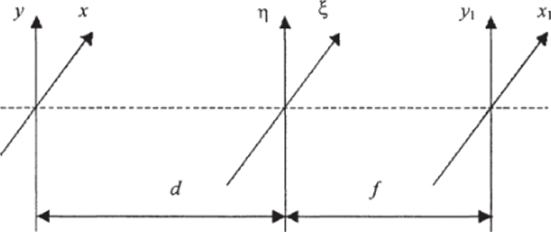
Рис. 1.7. Плоскости пересчета.