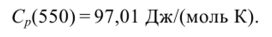Интерполяционные многочлены Ньютона

Рассмотрим понятие конечных разностей.

Пусть задана функция у=f{x) на отрезке [х₀, х"], который разбит на п одинаковых отрезков (случай равноотстоящих значений аргумента): Ax=h = const. Для каждого узла х₀, х, =х₀ + /г, …, х" =х₍₎ + п h определены значения функции в виде Введем понятие конечных разностей.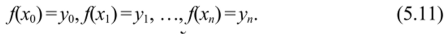

Конечные разности первого порядка.

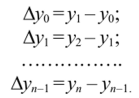
Конечные разности второго порядка 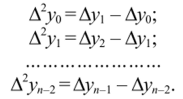Аналогично определяются конечные разности высших порядков: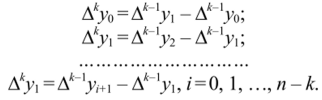

Конечные разности функций удобно располагать в таблицах, которые могут быть диагональными (табл. 5.1) или горизонтальными (табл. 5.2).

Диагональная таблица

Таблица 5.1.

Горизонтальная таблица

Таблица 5.2.

Первая интерполяционная формула Ньютона

Пусть для функции у=/(х) заданы значения у, =/(х,) для равностоящих значений независимых переменных:

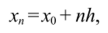
где h — шаг интерполяции.

Необходимо найти полином Р"{х) степени нс выше п, принимающий в точках (узлах) х, значения:

Интерполирующий полином ищется в виде: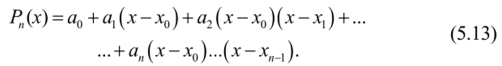

Задача построения многочлена сводится к определению коэффициентов а, из условий:

Полагаем в (5.13) х=х₀, т. к. второе, третье и другие слагаемые равны 0, то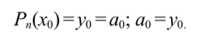

Найдем коэффициент а_{.

Приэс=Х1 получим:

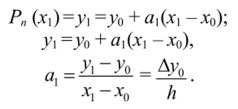
Для определения а₂ составим конечную разность второго порядка. При х=х₂ получим:

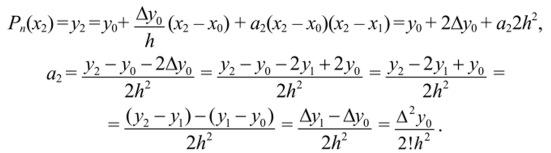
Аналогично можно найти другие коэффициенты. Общая формула имеет вид:

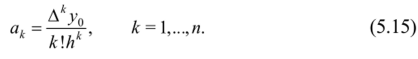
Подставляя эти выражения в формулу (5.13), получаем:

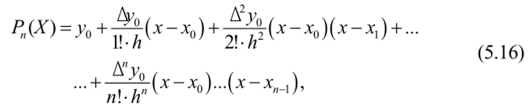
где х" у_х — узлы интерполяции; х — текущая переменная; h — разность между двумя узлами интерполяции; h — величина постоянная, т. е. узлы интерполяции равно отстоят друг от друга.

Этот многочлен называют интерполяционным полиномом Ньютона для интерполяции в начале таблицы (интерполирование «вперед»), или первым полиномом Ньютона.

Для практического использования этот полином записывают в преобразованном виде, вводя обозначение t=(х — x₀)/h, тогда.

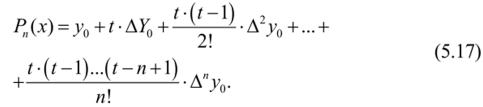
Эта формула применима для вычисления значений функции для значений аргументов, близких к началу интервала интерполирования.

Блок-схема алгоритма метода Ньютона для интерполирования «вперед» приведена на рис. 5.3, программа — в приложении.

Пример 5.3. Дана таблица значений теплоемкости вещества в зависимости от температуры C_p=f{T) (табл. 5.3).

Таблица 5.3.

Построить интерполяционный многочлен Ньютона для заданных значений функции: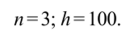

Составим таблицу конечных разностей функции (табл. 5.4).

Таблица 5.4.

Воспользуемся формулой (5.16):

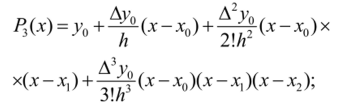
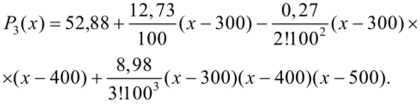
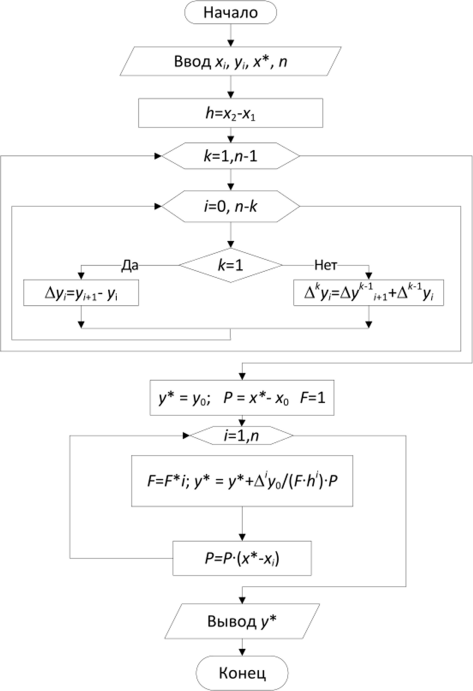
Рис. 5.3. Блок-схема алгоритма метода Ньютона для интерполирования «вперед»

После выполнения преобразований получим интерполяционный многочлен вида: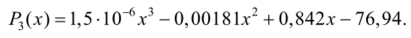

Полином имеет третью степень и дает возможность вычисления при помощи найденной формулы значения у для неизвестного х.

Пример 5.4. В табл. 5.3.1 приведены значения теплоемкости в зависимости от температуры. Определить значение теплоемкости в точке Г=450 К.

Воспользуемся первой интерполяционной формулой Ньютона. Конечные разности рассчитаны в предыдущем примере (табл. 5.3.2), запишем интерполяционный многочлен при х=450 К:

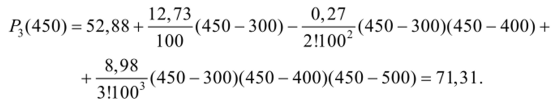
Таким образом, теплоемкость при температуре 450 К будет.

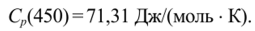
Значение теплоемкости при Г=450 К получили такое же, что и рассчитанное по формуле Лагранжа.

Вторая интерполяционная формула Ньютона

Для нахождения значений функций в точках, расположенных в конце интервала интерполирования, используют второй интерполяционный полином Ньютона. Запишем интерполяционный многочлен в виде.

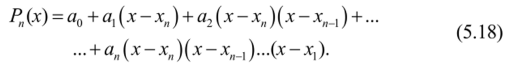
Коэффициенты а₀, а_ь …, а" определяем из условия:

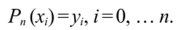
Полагаем в (5.18) х=х", тогда.

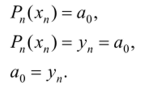
Полагаем х=х"_|, тогда 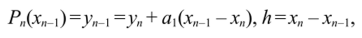следовательно,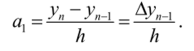

Если x⁼x_n-₂i то.

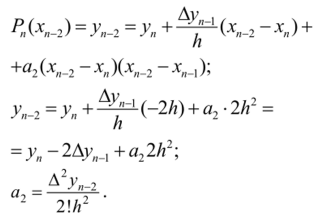
Аналогично можно найти другие коэффициенты многочлена (5.18):

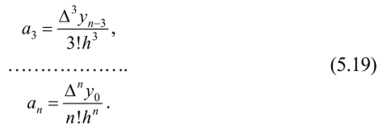
Подставляя эти выражения в формулу (5.18), получим вторую интерполяционную формулу Ньютона, или многочлен Ньютона для интерполирования «назад»:

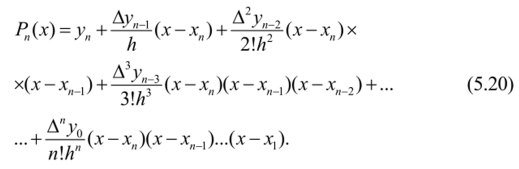
Введем обозначения: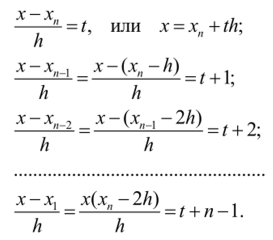

Произведя замену в (5.19), получим:

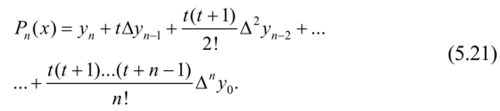
Это вторая формула Ньютона для интерполирования «назад».

Пример 5.5. Вычислить теплоемкость (см. табл. 5.3) для температуры Г=550 К.

Воспользуемся второй формулой Ньютона (5.19) и соответствующими конечными разностями (см. табл. 5.4):

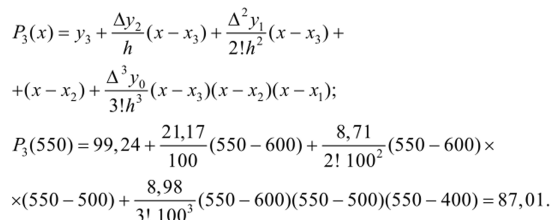
Следовательно, значение теплоемкости при температуре 550 К равно