Синтетическая классификация марковских цепей и моделей риска

Объединяя приведенные выше классификации марковских процессов, па основе квадрографа времени можно записать выражение.

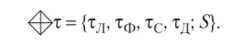
Таким образом, получим как простые, так и сложные (комбинированные) классы МП в виде многосвязного графа (рис. 13.6). С учетом примеров 2-го и 3-го классов (см. их выше) дадим новую классификацию марковских случайных процессов, связанных с введением квадрографа времени в АТН. Из приведенной на рис. 13.6 диаграммы (графа) очевидны новые классификационные типы, порождающие марковские модели надежности комбинированного типа. Например, ясно, что новые модели можно получить как комбинации элементарных моделей, расставленных по углам графа: 0(т_ф), 0(т_л), А (т_л), А (т_с). В круглых скобках на рис. 13.6 приведены номера моделей (номера 1—6 согласно Вентцель и Овчарову), перечисленных выше.

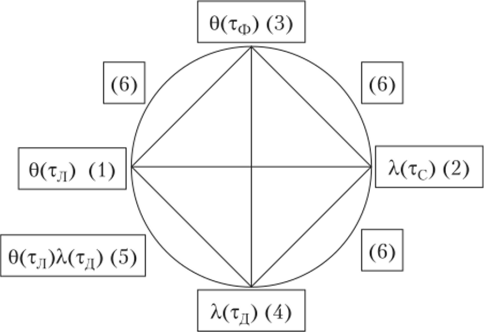
Рис. 13.6. Многосвязный граф классификации марковских процессов

• (и моделей рисков):
  • 1—6 — номера видов (классов) МП; 0 и X соответственно отображают дискретные и непрерывные состояния технических систем, описываемых МП

Отсутствие классификации моделей риска сильно затрудняет работу исследователей в этом направлении. В частности, в сфере страхования объектов это актуально. Сам Марков по просьбе финансистов и экономистов построил интересную модель страхования жизни человека, основываясь на статистике по ее продолжительности, т. е. модель риска. Однако вопросами классификации он не занимался. И сколько-нибудь удовлетворительных классификаций, за исключением математической классификации Колмогорова, на основе его цепей не построено.

Учитывая важность оценок рисков во времени, целесообразно использовать предложенную нами классификацию МП в качестве классификации моделей риска объектов после задания граничных значений их показателей. Достоинством такой классификации является очевидная ее связь с предложенной нами концептуальной АТЫ^[1].

Для решения задач, но Марковским процессам широко используется теория матриц, приведем некоторые важные понятия, необходимые для усвоения очень хорошей книги О. С. Андросенко [2], содержащей краткий теоретический материал и контрольные задания, но марковским цепям с дискретным и непрерывным временем. Указания содержат необходимые инструкции для решения задач с применением общедоступных пакетов программ WinQSB и MathCAD.

• 1. Неотрицательная матрица (НМ) — прямоугольная таблица с неотрицательными элементами, взятыми из множества действительных чисел.
• 2. Вещественный вектор — неотрицательный вектор (строчная матрица), с неотрицательными элементами, которые взяты из множества действительных чисел.
• 3. Стохастическая матрица (СМ) — это ИМ, у которой сумма элементов каждой ее строки равна 1.
• 4. Цепь Маркова (ЦМ) — строчная матрица, составленная из марковских элементов, взятых из множества действительных чисел; ЦМ возникает повторением марковских элементов, или, что-то же, условных вероятностей. Их называют вероятностями перехода некоторой дискретной последовательности случайных величин 0_О —> 0| —> 0₂ —> 0з —> … —" 0_И —> —>… —> 0"_! в состояние 0_Л в дискретные моменты времени, обозначаемые чаще всего как n_n(0,j0_w_j) = 7i_w(0j0_o, 0_1? …, 0р, …, 0"_i), которые образуют простую ЦМ из множества действительных чисел.
• 5. Марковский элемент (марковское свойство) = условная вероятность = переходная вероятность = одношаговая вероятность,…, m-шаговая вероятность.
• 6. Граф размеченный (ГР) — графическое состояние стохастической системы, отображаемое графом се состояний (ГС); на ГС кружочками или прямоугольниками обозначают состояния системы, а стрелками — возможные ее переходы из одного состояния в другое (непосредственно, а не через некое иное состояние).Число состояний может быть как конечным, так и бесконечным, но счетным.
• 7. Матрицы соответствующие — матрицы, при умножении которых соблюдается соотношение их порядков «множимого» и «множителя»¹, т. е. число столбцов (р) первой матрицы равно числу строк (р) второй матрицы: [т, р] • [/;, п] = [т, п] (порядок матрицы определяется количеством строк и столбцов в прямоугольной таблице).

Пример 13.1

(0,7 0,3).

Задана матрица л, = вероятностей перехода дискретной цепи Маркова.

^0,6 0,4.

из го состояния в j-с за один шаг (i, j = 1, 2). Распределение вероятностей по состояниям в начальный момент t = 0 определяется вектором (матрицей-строкой) q = = (0,1 0,9). Требуется найти: 1) матрицу финальной вероятности Р₂ перехода цепи из состояния i в состояние j за два шага; 2) матрицу финальной вероятности Р, перехода цепи из состояния i в состояние j за один шаг.

Решение. В случае однородности дискретной цепи Маркова для нее справедливо соотношение² к_п = л?, где — матрица переходных вероятностей за один шаг; — матрица переходных вероятностей за п шагов; для п = 2 вычислим произведение матриц³:

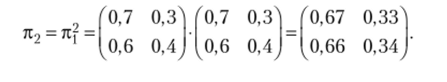
• 1 См.: Современная математика для инженеров / пер. с англ, под общ. ред. И. II. Векуа. М.: Иностранная литература, 1958. С. 308.
• 2 См.: Вентцель Е. С. Исследование операций. М.: Советское радио, 1972. С. 181—232. По нашему мнению, лучше этой книги, написанной женской рукой, но ясности для практико-математических применений марковских цепей и процессов никто не написал.
• 3 См.: Ганггтахер Ф. Р. Указ. соч. С. 17.

Пример 13.2.

Имеется матрица интенсивностей переходов непрерывной цени Маркова.

" -2 1 П Л= 2 -3 1. Требуется составить размеченный граф состояний, соответствую;

_к4 О -А)

щий матрице Л, и систему дифференциальных уравнений Колмогорова для вероятностей состояний; найти предельное распределение вероятностей.

Решение. Однородная цепь Маркова с конечным числом состояний Л₂, …, А_к характеризуется матрицей интенсивностей переходов.

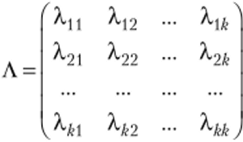
где X_{i = lim • ^ ^ — интенсивность перехода цени Маркова из состояния Д в состоя;

⁹ д/-«о At

нис Д; Pjj (At) — вероятность перехода Д —> Д за интервал времени At.

Переходы системы из состояния в состояние удобно задавать с помощью размеченного графа состояний, на котором отмечаются дуги, соответствующие интенсивностям Xjj > 0.

Составим размеченный граф состояний для заданной матрицы интенсивностей переходов (рис. 13.7). Пусть pit) = (p_{(At), p₂(At),…, p_k(At)) — вектор вероятностей Pj (t), j =1,2,…, k, нахождения системы в состоянии Д в момент t.

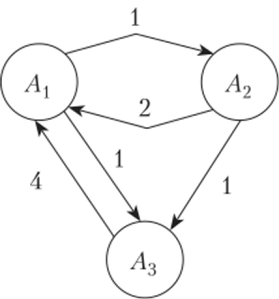
Рис. 13.7. Размеченный граф состояний.

Очевидно, что 0 <Pj (t) < 1 и p'(t) = (p[(t), p'₂(t),…, pl (t)). Вероятностиpj (t) удовлетворяют системе дифференциальных уравнений Колмогорова на базе марковских цепей (СДУМК), которая в матричной форме имеет вид.

p'(t) = p (t)A. (13.1).

Если в начальный момент система находилась в состоянии А_)У то СДУМК следует решать при начальных условиях.

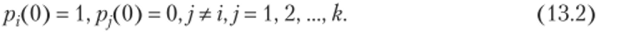
Совокупность СДУМК (13.1) и начальных условий (13.2) однозначно описывает однородную цепь Маркова с непрерывным временем и конечным числом состояний. Составим СДУМК для заданной цепи Маркова. Поскольку к = 3, то у = 1, 2, 3. Из соотношения (13.1) получим.

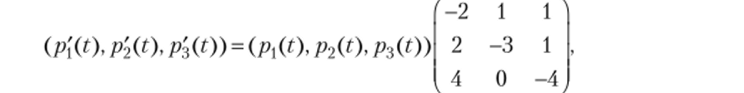
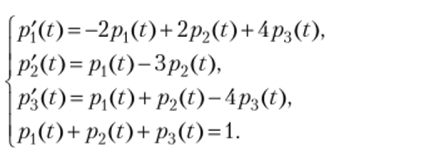
отсюда имеем систему Последнее условие называется нормировочным.

Распределение вероятностей по состояниям называется стационарным, если оно не меняется с течением времени, т. е. p'(t) = р' = 0.

Тогда из СДУМК (13.1) получаем систему для нахождения стационарного рас;

_ к

пределения рА = 0, где? р_} —1, 0 < р_} < 1.

М Для данного примера из МСДУК получим.

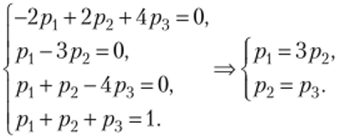
г о, 1 ^и 131.

С учетом нормировочного условия ор₂ + /Ъ + Рг ~ 1 найдем р-_} = —, р, =—, р_:> = —

5 5 5.

Следовательно, предельное распределение имеет вид р = .

5 5 5)

Отмстим, что этот результат может быть получен непосредственно по размеченному графу состояний. Для этого надо воспользоваться правилом: для стационарного распределения сумма произведений kjp_itj Ф /', для стрелок, выходящих из /'-го состояния, равна сумме произведений Xjp^j ФI, для стрелок, входящих в /-е состояние. Действительно,.

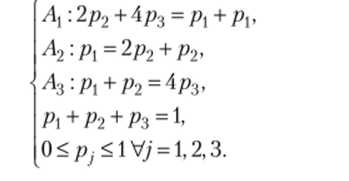
Выходит, что полученная система эквивалентна той, которая составлена по МСДУК. Следовательно, она имеет такое же решение. Ответ: стационарное рас;

— (³ 1 О пределение имеет вид р= —.

у 5 5 5 ,.

Система S представляет собой вычислительный центр (ВЦ), в котором имеется три ЭВМ. В определенные моменты времени все ЭВМ осматриваются, в результате чего каждая признается либо исправной и продолжает работать, либо неисправной и направляется в ремонт. Вероятность того, что исправная ЭВМ выйдет из строя, равна q. Вероятность того, что неисправная ЭВМ будет приведена в исправное состояние, т. е. восстановлена, равна г.

Процессы выхода ЭВМ из строя и их восстановления протекают независимо друг от друга. Размеченный граф состояний ВЦ имеет вид, показанный на рис. 13.8.

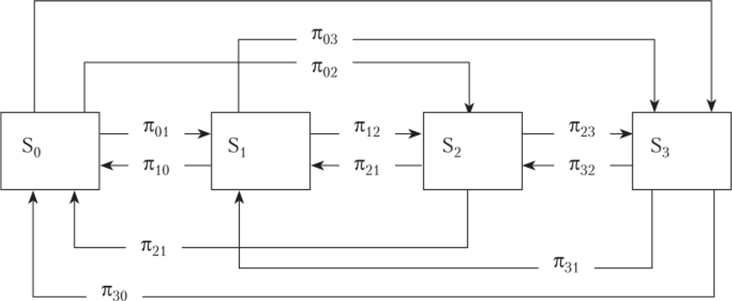
Рис. 13.8. Размеченный граф состояний ВЦ.

Па рис 13.8 обозначены следующие состояния ВЦ: s₀ — все три ЭВМ исправны;

s, — одна ЭВМ неисправна, остальные две работают; s₂ — две ЭВМ неисправны, одна работает; s₃ — все три ЭВМ неисправны.

Стрелки на рис. 13.8, которые идут слева направо, отображают прямое движение потока вероятностей — это вероятности перехода я₀, системы из состояния s₀ в состояние s,-. Эти вероятности находятся согласно биномиальному распределению:

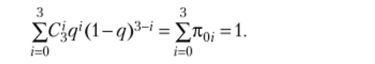
Возвратные вероятности восстановления ВЦ отображаются симметричной формулой:

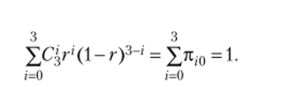
Формулы, аналогичные приведенным, используются для получения системы уравнений переходных вероятностей и n_jr

После решения системы уравнений находятся численные значения финальных вероятностей состояний ВЦ: р₀ = 0,216,/;, = 0,432,р₂ ~ 0,288, р₃ = 0,064 при г- 0,3; q = 0,2.

Примечание. Подобные задачи решаются с использованием компьютерных программ.^[2]

• [1] При решении задач полезными книгами, посвященными теории и практике использования матриц, могут послужить следующие: Гантмахер Ф. Р. Теория матриц. М.: Наука, 1967; Андросенко О. С., Девятченко Л. Д., Манченко Е. П. Постановка и решение задач марковских процессов на ЭВМ: Методические указания и варианты контрольных заданий для студентов всех специальностей. Магнитогорск: ГОУ ВПО «МГТУ», 2007.
• [2] См.: Вентцелъ Е. С., Овчаров Л. А. Теория случайных процессов и ее инженерные применения. С. 125 127.