Методы термодинамических исследований

Термодинамические исследования физических явлений могут быть осуществлены при помощи двух методов: метода циклов и метода термодинамических потенциалов. Метод циклов или круговых процессов возник первым. Его использовали в своих исследованиях еще Карно, Клаузиус и др. Суть этого метода заключается в том, что для установления какой-либо закономерности определенного явления подбирается подходящий обратимый цикл и к этому циклу применяются уравнения первого и второго начал термодинамики. Чаще всего используется цикл Карно. Слабостью метода циклов является то, что всякий раз приходится подбирать подходящий цикл, а сам его выбор произволен.

Сейчас при исследованиях термодинамических свойств систем применяется, главным образом, метод термодинамических потенциалов (метод характеристических функций), предложенный Гиббсом (рис. 2.5.1). Основу метода составляет определение с помощью основного уравнения термодинамики (2.4.6) некоторых функций состояния в зависимости от выбора независимых переменных. Посредством этих функций и их производных могут быть явно выражены термодинамические свойства системы. При этом первые производные определяют термические свойства, а вторые — калорические. Найденные функции называются характеристическими [Яворский, Детлаф, 1974].

Например, при независимых переменных т| и V характеристической функцией является внутренняя энергия U (вывод см. далее). Характеристическая функция, убыль которой в равновесном процессе, протекающем при неизменных значениях определенной пары термодинамических параметров, равна полной работе, произведенной системой, за вычетом работы против внешнего давления, называется термодинамическим потенциалом.

Рис. 2.5.1. Гиббс Джоэайя Уилард (1839−1903) Американский физик, один из основателей термодинамики. Разработал теорию термодинамических потенциалов.

Существование характеристических функций (термодинамических потенциалов) вытекает из свойств полного дифференциала. В термодинамике обычно используется четыре термодинамических потенциала: внутренняя энергия, свободная энергия (энергия Гельмгольца), термодинамический потенциал Гиббса (энергия Гиббса) и энтальпия (теплосодержание).

Для их описания рассмотрим сначала равновесные системы, находящиеся только под всесторонним давлением. Тогда основное уравнение термодинамики выглядит так:

В (2.5.1) входят пять функций состояния: Т, tj, U, р и V. Состояние же простой системы определяется двумя параметрами. Поэтому если из пяти функций выбрать две в качестве независимых переменных, то окажется, что уравнение (2.5.1) содержит еще три неизвестные величины. Для их определения необходимо иметь еще два уравнения. Однако при некоторых независимых переменных основное термодинамическое выражение (2.5.1) позволяет найти три неизвестные функции, если иметь только лишь одно уравнение. Несколько примеров использования метода потенциалов приводятся ниже.

1. Независимые переменные энтропия t] и объем V. Для определения других функций состояния нужно знать только уравнение для внутренней энергии U как функции этих переменных:

Полный дифференциал внутренней энергии равен^[1]

Сравнивая уравнение (2.5.3) и выражение.

которое является следствием (2.5.1), получим:

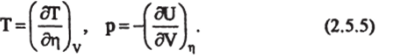
Продифференцируем первое уравнение в (2.5.5) по V, а второе — по.

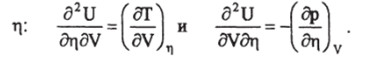
смешанные производные, получим:

Приравняв полученные.

Отсюда следует, что изменение температуры при адиабатическом расширении равно изменению давления при изохорном сообщении теплоты системе с обратным знаком. Установление связей типа (2.5.6) — суть метода термодинамических потенциалов.

Таким образом, внутренняя энергия U в переменных г| и V является характеристической функцией, так как функции состояния Т и р определяются с ее помощью по формулам (2.5.5)². Она же в этих переменных называется также термодинамическим потенциалом. Функция U=U (n, V) как термодинамический потенциал мало пригодна в практических исследованиях, так как одна из независимых переменных, энтропия т|, не может быть непосредственно измерена.

2. Независимые переменные Т и V. Преобразуем уравнение (2.5.1) таким образом, чтобы в него входили дифференциалы <�ГГ и dV. Для этого вычтем из обеих частей уравнения (2.5.1) дифференциал d (Tr)=Tdr|+TidT. Получим:

Из равенства (2.5.11) следует, что изменение энтропии при се изотермическом расширении равно изменению давления при изохорном нагревании.

Функция F называется свободной энергией (энергией Гельмгольца) и является характеристической функцией (термодинамическим потенциалом) в переменных V и Т^[2][3]. Свободная энергия при изотермических процессах играет роль внутренней энергии при адиабатических процессах. Как видно из (2.5.9), при изотермических процессах работа совершается системой не за счет убыли внутренней Характеристическая функция G (T, p) называется термодинамическим потенциалом Гиббса (энергией Гиббса)'. Эта функция имеет важное значение в термодинамике, так как она определяется через легко измеряемые переменные р и Т.

Вторые производные функции G (T, p) дают уравнение.

4. Независимые переменные т] и р. Перейдем в уравнении (2.5.1) к дифференциалам <| и р, прибавив к обеим частям уравнения дифференциал d (pV). Имеем:

¹ Если за независимые переменные принять температуру Т и обобщенные силы А, сопряженные внешним параметрам а, то энергия Гиббса для сложных П.

систем равна G = U-Тц +? А,-а, а ее дифференциал энергии U, а за снег убыли функции F. Величина Тт} называется связанной энергией.

3. Независимые переменные Тир. Для перехода к переменным Т и р в уравнение (2.5.1) прибавим к обеим частям дифференциал d (pV)=pdV+Vdp. Применив преобразование Лежандра, получим:

Обозначив.

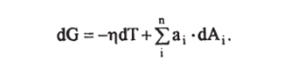
получим.

Функция (2.5.17) называется энтальпией^[4][5]. Энтальпия является термодинамическим потенциалом при независимых переменных т) и р, поскольку ее производные равны:

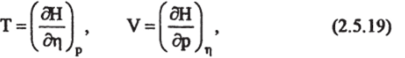
а повторное дифференцирование энтальпии и приравнивание вторых производных вида дает:

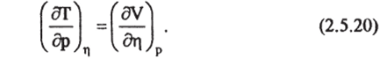
При изобарических процессах изменение энтальпии равно поглощенному количеству теплоты:

(<�Ш)_р = (Tdn)_p = (6Q)_P = C_pdT, (2.5.21).

где.

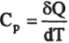
— теплоемкость при постоянном давлении. По этой причине энтальпию называют также тепловой функцией или теплосодержанием.

Из (2.5.21) имеем Различные термодинамические потенциалы можно определить через другие. Так, зависимость внутренней энергии от свободной энергии можно получить из уравнений (2.5.8) и (2.5.10):

Связь энтальпии с термодинамическим потенциалом можно установить с помощью уравнений (2.5.13) и (2.5.14):

Уравнения (2.5.23) и (2.5.24), устанавливающие связь между различными термодинамическими потенциалами, называются уравнениями Гиббса-Гельмгольца.

Отметим, что в рамках термодинамики нельзя найти явные выражения для термодинамических потенциалов. Однако начала термодинамики позволяют найти связи одних свойств систем с другими их свойствами типа (2.5.6), (2.5.11), (2.5.15), (2.5.20). Такие соотношения называются основными уравнениями или соотношениями Максвелла. Другие соотношения типа соотношений Максвелла легко могут быть получены на основании применения якобианов [Гугтенхейм, 1950].

Все термодинамические потенциалы обладают аддитивными свойствами и являются однозначными функциями состояния, причем их уменьшение при соответствующих условиях определяет работу

системы против действующих на нее сил.

До этого все исходные положения и начала термодинамики относились к термодинамическим системам, состоящим из одного компонента. Однако в природе имеются системы с двумя или более компонентами, причем число молей в них или общее число молей системы могут изменяться. Состояние таких систем характеризуется не только внешними параметрами а^…, 2^ и температурой Т, но и числом молей каждого компонента N_1? …, N_R или соответствующими молярными концентрациями х_х =^/^Ы_к .

/ к=1.

Основное уравнение термодинамики для систем, состоящих из нескольких компонентов, при равновесных процессах

' п Л.

5Q = Tdr|, 6W = V А, • da, принимает вид

w i=l >

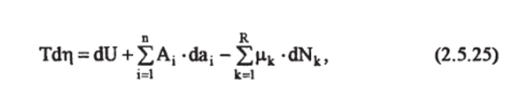
где dN_k = d_cN_k +djN_k — изменение числа молей к-ого компонента, обусловленное обменом с окружающей средой и химическими.

(ди).

реакциями соответственно; ц_к = - - так называемый.

химический потенциал k-ого компонента.

Для обратимых процессов, совершаемых гомогенной Rкомпонентной системой, состав и масса которой могут изменяться и на которую действует только всестороннее давление, термодинамические потенциалы равны:

Из уравнений (2.5.26) — (2.5.29) следует, что химический потенциал имеет вид Химический потенциал служит количественной мерой способности компонента к переходу: в системе, не находящейся в равновесии, любой компонент стремится перейти из тех участков системы, где его потенциал больше, в те части системы, где потенциал меньше [Эдсолл, Гатфрснд, 1986]. Химический потенциал — величина интенсивная. Она не зависит от размера системы, а зависит только от внешних параметров, ее состава и температуры. Эго следует нз аддитивности всех термодинамических потенциалов. В случае однокомпоненпюй системы при изменении числа молей N в некоторое число раз величины термодинамических потенциалов изменяются во столько же раз. Следовательно, аддитивная термодинамическая величина является однородной функцией первого порядка относительно аддитивных переменных.¹ Отсюда следует, что:

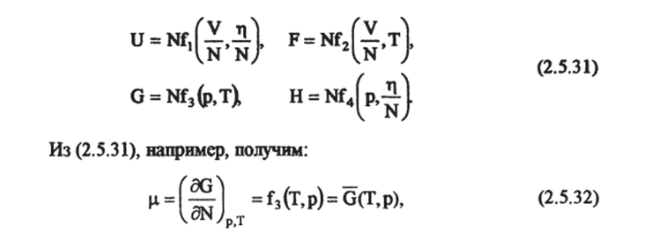
т.е. химический потенциал равен энергии Гиббса на один моль вещества. Сравнивая выражения (2.5.31) и (2.5.32), имеем.

Как видно из формулы (2.5.32), химический потенциал не зависит от числа молей, а определяется только давлением (внешними параметрами) и температурой.

Для смеси веществ, состоящих из N_lf N₂,… молей,.

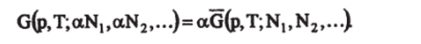
Дифференцируя это равенство по, а и полагая а=1, получим.

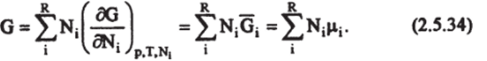
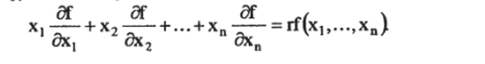
‘функция f (xi,…, x") есть однородная функция степени г относительно аргументов xi,…, x", если f (axi,…, axn)=a^rf (xi,…, Xn). Из теоремы Эйлера об однородных функциях следует:

Так как внутренняя энергия U является однородной функцией первого порядка и зависит только от экстенсивных независимых параметров, то по теореме Эйлера об однородных функциях для равновесных термодинамических систем, находящихся под действием всестороннего давления имеем.

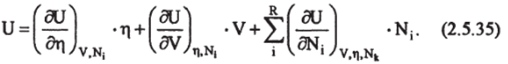
Сравнивая уравнения (2.S.26) и (2.S.3S), получим.

Продифференцировав (2.5.36) как функцию параметров r|, Т, v, р, N" и ц, а также учитывая (2.5.26), находим важное в термодинамике.

уравнение Гиббса-Дюгема.

• [1] ‘Индексы у скобок означают постоянство указанных параметров. 2Для сложных систем, состояние которых определяется обобщеннымикоординатами (внешними параметрами ai, и энтропией ц), термодинамическим потенциалом будет внутренняя энергия U (n;ai. д,), П дифференциал которой равен <�Ш =Тбг|-?А;(1а; .
• [2] Подобные преобразования называются преобразованиями Лежандра.
• [3] Для сложных систем, состояние которых определяется внешнимипараметрами ai,, ап и температурой Т энергия Гельмгольца равна F=U-Tti, а ее П дифференциал dF = -r|dT-?A, da,. i
• [4] 1 Для сложных систем при независимых переменных Г| и А, энтальпия равна П П Н = U +? А, — а, а ее дифференциал <1Н = Tdr| + ?a, -dAj.
• [5] i