Семейства линейных рекуррентных последовательностей

Для заданного нормированного многочлена f (x)? F_q[x], /о Ф О, через S (f) обозначим множество всех линейных рекуррентных последовательностей с характеристическим многочленом f (x). Так как при заданном характеристическом многочлене линейная рекуррентная последовательность однозначно определяется начальным состоянием, то |5(/)| = q^m, где т = degf (x).

Множество S (f) можно рассматривать как векторное пространство с естественными операциями покоординатного (почленного) сложения и умножения на элемент поля F_q.

Теорема 6.3. Пусть d (x) — произвольный нормированный делитель многочлена f (x). Тогда в множестве S (f) существует линейная рекуррентная последовательность, минимальный многочлен которой равен d (x).

Доказательство. Так как множество аннулирующих многочленов заданной линейной рекуррентной последовательности над полем F_q является идеалом кольца F_q[x], см. утверждение 6.6, имеет место включение S (d) С ?(/)• Теперь справедливость теоремы вытекает из того, что в множестве S (d) имеется линейная рекуррентная последовательность, минимальный многочлен которой равен d (x). ?

Теорема 6.4. Пусть f (x), /2(0:),…, ft{x) ? F^[x] - нормированные многочлены, не являющиеся постоянными. Тогда

Теорема 6.5. Пусть t ? N линейных рекуррентных последовательностей Що, щд,.г = 1,…, t, заданы над полем своими минимальными многочленами т{х),…, mt (x)? F_q[х] и имеют, соответственно, минимальные периоды т,…, r_t.

Если многочлены т (х),…, гаДх) попарно взаимно просты, то минимальный период г и минимальный многочлен т (х) последовательности, являющейся суммой значений

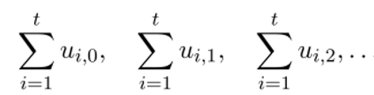
равны, соответственно,.

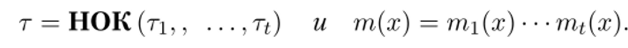
Доказательство сформулированных теорем может быть найдено в монографии [3].

Рассмотрим несколько примеров, иллюстрирующих сформулированные выше результаты.

Пример 6.3. Найдем минимальный период линейной рекуррентной последовательности над полем F2 с характеристическим многочленом f (x) = X^s + х + 1 и вектором начального состояния s = (so, si, s₂) ⁼ (°iM);

Пусть г — минимальный период линейной рекуррентной последовательности, т (х) — ее минимальный многочлен. Тогда верно равенство г = и (т (х)). Так как минимальный многочлен т (х) является делителем характеристического многочлена f (x) = х³+х+1, который неприводим над полем F2, то т (х) = f{x). При этом случаю т (х) = 1 отвечает линейная рекуррентная последовательность с нулевым вектором начального состояния. Таким образом, Г — ы (1) — 7.

Пример 6.4. Найдем минимальный многочлен т (х) для линейной рекуррентной последовательности, заданной характеристическим многочленом f (x) = х³ +1 Е F2[cc] и заданным начальным вектором * = ( 1,0,1).

Рассмотрим последовательность векторов-состояний линейной рекуррентной последовательности:

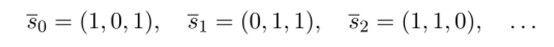
В этой последовательности минимальное значение к, при котором вектор является линейной комбинацией векторов «^'о?¹⁹ • • • 9 &к—1 * равно 2.

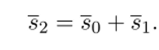
Отсюда т (х) = х² + х + 1.

Пример 6.5. Найдем множество возможных минимальных периодов, отвечающих семейству S (f) линейной рекуррентной последовательности над нолем F2 с характеристическим многочленом.

f (x) = (х³ + х + 1){х² + х + 1).

Так как для любого делителя d (x) многочлена f (x) в множестве S (f) найдется линейная рекуррентная последовательность с минимальным многочленом т (х) = d (x), го искомое множество В минимальных периодов семейства S (f) совпадает с множеством периодов делителей d (x) характеристического многочлена /(ж). Имеем.

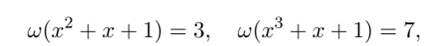
тогда w (/) = НОК (3, 7) = 21 и R = {1,3,7,21}.

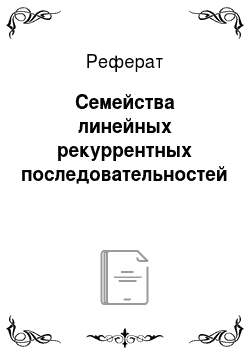
Пример 6.6. Найдем первые три бита вектора 56-го состояния s, 56 линейной рекуррентной последовательности 15-го порядка с характеристическим многочленом /(ж) = (ж³ + ж + I)⁵ и вектором начального состояния «о = (ПО, 1,1,0,0,…, 0).

Минимальный многочлен линейной рекуррентной последовательности является делителем многочлена /(ж), следовательно, период многочлена /(ж) будет и периодом, но не обязательно минимальным. Имеем: ш (/) — 2³са (ж³ + ж + 1) = 8- 7 = 56. Отсюда