Синтез цифровых фильтров

Постановка задачи синтеза дискретных фильтров не отличается от задачи синтеза аналоговых фильтров, и ее решение состоит из двух этапов: этапа аппроксимации и этапа реализации [31].

На этапе аппроксимации отыскиваются физически реализуемые математические выражения для комплексной (операторной) передаточной функции или импульсной характеристики, которые приближенно воспроизводят заданные в виде графиков или таблиц частотные или временные характеристики дискретной цепи.

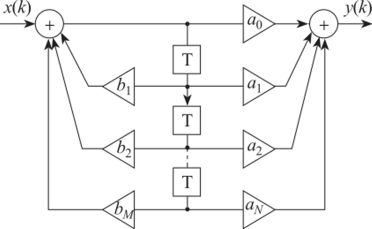
Рис. 7.43.

На этапе реализации по найденному математическому выражению конструируется цифровая цепь, например, в виде каскадного или параллельного соединения простых цифровых структур.

При рассмотрении первого этапа отдельно остановимся на решении задачи аппроксимации для БИХи КИХ-фильтров. Это вызвано следующими причинами.

• 1. При аппроксимации БИХ-фильтров можно использовать богатый опыт проектирования аналоговых фильтров. В частности, наиболее распространенные методы основаны на использовании характеристик аналогового фильтра-прототипа (метод инвариантности импульсной характеристики и метод билинейного z-преобразования). Для КИХ-фильтров не найдено непосредственных аналогов среди пассивных электрических фильтров, и методы их синтеза относятся к прямым методам (метод частотной выборки или метод на основе временных окон).
• 2. Операторные передаточные функции БИХ-фильтров являются дробнорациональными функциями, тогда как в случае КИХ-фильтров их необходимо аппроксимировать полиномиальными функциям.
• 3. Возможно, в отличие от БИХ-фильтров, построить КИХ-фильтры с линейной фазовой характеристикой, что налагает определенные условия на решение задачи аппроксимации их характеристик.

Остановимся на одном методе синтеза дискретных систем, методе билинейного z-преобразования. Данный метод применяется при синтезе рекурсивных (БИХ) фильтров. Достоинство метода состоит в том, что при синтезе ЦФ используются достижения, полученные при синтезе аналоговых фильтров: расчетные соотношения, таблицы и графики.

В основу метода билинейного z-преобразования положено специальное преобразование комплексной переменной, в результате которого переменная р заменяется на переменную z, а передаточная функция аналоговой цепи Н (р) переходит в операторную передаточную функцию H (z) цифровой системы. При преобразовании характеристик аналоговой цепи с целью получения H{z) должны выполняться следующие требования:

H (z) должна быть физически реализуемой функцией;

если аналоговый фильтр устойчив, то преобразование должно приводить к устойчивому цифровому фильтру;

существенные свойства аналоговой частотной характеристики должны сохраняться в частотной характеристике получающегося в результате преобразования цифрового фильтра.

Пусть задана операторная передаточная функция аналогового фильтра Н (р) и необходимо получить H (z) цифрового фильтра. Воспользуемся соотношениями, устанавливающими взаимосвязь между zи р-плоскостями:

Прямая подстановка последнего уравнения в выражение Н (р) приведет к иррациональной H (z) цифрового фильтра, которая не может быть реализована в виде дискретной линейной системы.

Поскольку точно решить задачу не удается, то используем приближенный подход. Представим (7.51) в виде ряда Тейлора:

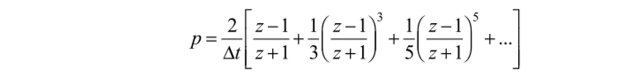
и для простоты ограничимся одним членом ряда где к = 2/At.

Соотношение (7.52) называют билинейным z-преобразованием, и оно широко применяется при проектировании ФНЧ, ФВЧ и полосовых цифровых фильтров.

Видно, что (7.52) является дробно-рациональной функцией, и ее подстановка в физически реализуемую Н (р) будет приводить в результате алгебраических преобразований также к физически реализуемой дробно-рациональной H (z) цифрового фильтра, т. е. первое требование, предъявляемое к H (z), будет выполняться.

Выясним, как билинейное z-преобразование трансформирует АЧХ цифрового фильтра. Для этого достаточно установить связь между значениями частот со на мнимой оси (а = 0) плоскости р и величинами шАt на единичной окружности z-плоскости. Подставив в формулу (7.52) р = /со и z = е'^шЛ', получим.

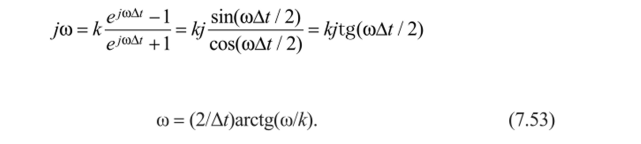
или Алгоритм расчета ЦФ по методу билинейного преобразования следующий.

Задаются исходные данные к ЦФ (значение частоты дискретизации, граничных частот полос пропускания и задерживания, а также величины ослаблений на этих частотах).

Требования к ЦФ преобразуются с помощью формулы (7.53) в требования к аналоговому фильтру.

С помощью справочников либо таблиц рассчитывается операторная передаточная функция Н{р) аналогового фильтра.

С помощью соотношения (7.51) в Н (р) производится замена переменной р. В результате получается искомая функция #(z).