Интегральное уравнение энергии ламинарного пограничного слоя
Пусть расход жидкости в направлении оси х через грань 3−4 меньше, чем через грань 1−2. Но при постоянной плотности эта разность расходов должна компенсироваться расходом через грань 2−4. Следовательно, через грань 2−4 будет выходить жидкость в количестве, равном разности расходов через грани 1−2 и 3−4. Жидкость вынесет с собой теплоту, равную. Вывод интегрального уравнения для теплового… Читать ещё >
Интегральное уравнение энергии ламинарного пограничного слоя (реферат, курсовая, диплом, контрольная)
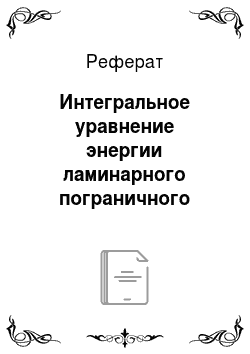
Выделим (рис. 16.6) в потоке жидкости контрольный элемент с размерами И > Д в направлении оси у, dx в направлении оси х и 1 в направлении оси z. Обозначим скорость набегающего потока через его избыточную температуру через (c)" = ТЛ — Tw, переменную скорость и избыточную температуру соответственно через wx и 3 = Т — Tw.
Вывод интегрального уравнения для теплового пограничного слоя производится аналогично выводу интегрального уравнения для динамического пограничного слоя (16.12). Разница состоит только в том, что вместо потоков количества движения рассматриваются потоки теплоты. Составим тепловой баланс для выделенного элемента.
Количество теплоты, вносимое жидкостью через грань 1−2, можно представить в виде:
Изменение этого количества теплоты на пути dx.
Рис. 16.6. К выводу интегрального уравнения энергии для ламинарного пограничного слоя
можно рассматривать как разность потоков теплоты через грани 1−2 и 3−4.
Пусть расход жидкости в направлении оси х через грань 3−4 меньше, чем через грань 1−2. Но при постоянной плотности эта разность расходов должна компенсироваться расходом через грань 2−4. Следовательно, через грань 2−4 будет выходить жидкость в количестве, равном разности расходов через грани 1−2 и 3−4. Жидкость вынесет с собой теплоту, равную.
Количество теплоты, отданное стенке жидкостью через грань 1−3:
Уравнение теплового баланса для выделенного элемента 1−2-3−4 с учетом (16.25)—(16.27) после сокращений и преобразований можно переписать в виде:
где а = ——коэффициент температуропроводности пластины.
рср Верхний предел h в (16.28) заменен на Л, так как при у = Л > Д подынтегральное выражение обращается в нуль.
Выражение (16.28) называют интегральным уравнением энергии пограничного слоя (получено Г. Н. Кружилиным) [10]. Это уравнение можно представить в следующей форме:
Интеграл в левой части уравнения называют толщиной потери энергии в тепловом пограничном слое конечной толщины Д и обозначают.
Эта величина иногда используется при определении числа Рейнольдса по толщине потери энергии в качестве характерного размера.
(Re-/=^).
V.
Метод исследования теплоотдачи с помощью интегрального уравнения энергии (16.28) приведен ниже.