Система произвольно расположенных сил

Момент силы относительно точки как вектор. Понятие момента силы относительно точки уже было сформулировано ранее [см. формулу (2.12)|. При решении пространственных задач момент силы удобнее изображать в виде вектора (рис. 2.20).

Вектор М₀ момента силы относительно точки О направлен перпендикулярно плоскости, проведенной через линию действия силы и эту точку.

Момент считается положительным, если при взгляде с вершины вектора представляется, что сила старается повернуть тело вокруг точки О по часовой стрелке.

Как видно из рис. 2.20, численная величина момента силы относительно точки может быть выражена не только известной зависимостью М₀ = Fh, но и удвоенной площадью треугольника АВО.

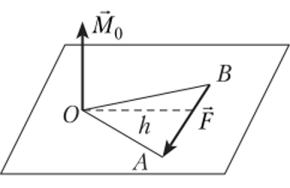
Рис. 2.20.

Момент силы относительно оси. Момент силы F относительно какойлибо оси и (рис. 2.21) определяется произведением проекции F_v силы F на плоскость I, перпендикулярную оси, на кратчайшее расстояние h (плечо силы относительно оси и) от F_v до точки пересечения оси с плоскостью:

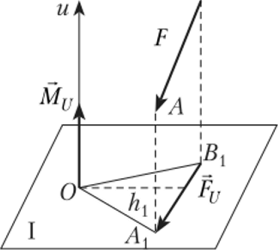
Рис. 2.21.

Момент силы Р_и относительно оси считается положительным, если при взгляде со стороны положительного направления оси представляется, что проекция силы старается повернуть тело вокруг этой оси по часовой стрелке.

Так же как и момент силы, момент силы относительно оси можно рассматривать как удвоенную площадь треугольника А_{В_хО (см. рис. 2.21).

Момент силы относительно оси равен нулю в двух случаях: если сила F параллельна оси и (F_v = 0) и если сила F пересекает ось и (h = 0).

Моменты силы относительно оси и точки связаны следующим образом: проекция момента силы относительно точки на ось, проходящую через эту точку, равна моменту силы относительно этой оси.

Действительно, из рис. 2.22 видно, что М₀= 2А, Му = 2А_и где А — площадь треугольника АВО, а А_х — площадь треугольника А_уВ_хО. Очевидно, что А_х = Асош, т. е. треугольник А_хВ_хО является проекцией треугольника АВО на плоскость I, и следовательно.

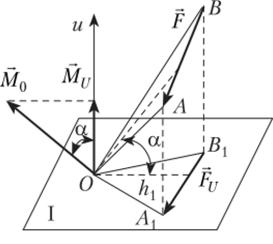
Рис. 2.22.

Приведение произвольной системы сил к заданному центру. Через вектор, изображающий силу в пространстве, и любую точку всегда можно провести плоскость. Поэтому для любого такого вектора можно воспользоваться правилом его переноса в пределах именно этой плоскости (см. подпараграф 2.3.3).

Таким образом, любую силу можно перенести параллельно начальному положению в любую точку (заданный центр приведения) пространства, добавив при этом пару, момент которой геометрически равен моменту данной силы относительно центра приведения.

Если в выбранный центр приведения перенести несколько пространственно расположенных сил, то получим две векторные системы:

• — систему сходящихся сил F_x, Р₂, f₂>
• — систему пар переноса М_1? М₂, М₃, М₄,… .

Произведя геометрическое сложение векторов указанных систем, получаем две векторные величины:

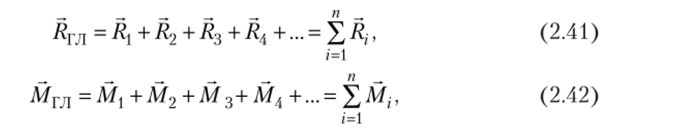
где R_VJl — главный вектор, а М_гл — главный момент относительно центра приведения.

Величина и направление главного вектора аналитически определяются по формулам (2.33)—(2.35):

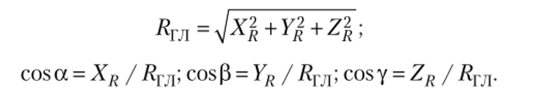
Главный момент М_гл, так же как и R_TJl, можно разложить по направлению координатных осей (рис. 2.23) и получить аналитические выражения его величины и направления:

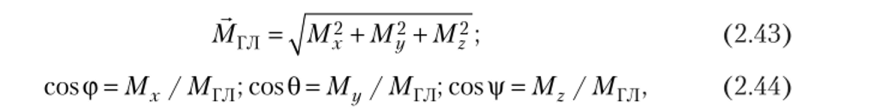
где ф, 0, |/ — углы, образованные направлением вектора главного момента и осями координат.

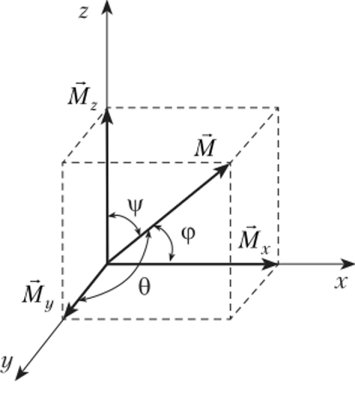
Рис. 2.23.

На основании формулы (2.40), показывающей зависимость между моментом относительно точки и моментом относительно произвольной оси, можно сделать вывод, что моменты М_х, М_у и М₂ есть главные моменты системы сил относительно осей координат.

Очевидно, что главный момент системы сил относительно оси координат равен алгебраической сумме моментов составляющих сил относительно той же оси:

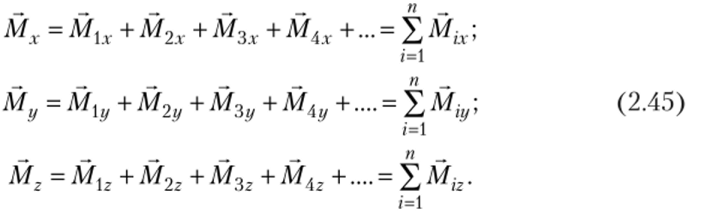
При приведении сил, произвольно расположенных в пространстве, к заданному центру возможны следующие случаи:

• — R_Yji Ф 0, М_гл * 0 — рассмотренный выше случай произвольной системы сил;
• — R_TJl 9*0, М_гл = 0 — система сил сразу приводится к равнодействующей благодаря удачно выбранному центру приведения на линии действия равнодействующей;
• — 7?_гл = О, М_гл Ф О — заданная система сил приводится к паре, плоскость действия которой перпендикулярна вектору главного момента;
• — Ry =0, М_гл = 0 — система сил находится в равновесии.

Первые три случая используются при решении инженерных задач, когда требуется привести к заданному центру активные силы, действующие на тело.

Условия равновесия системы произвольно расположенных сил. Итак, в случае равновесия и главный вектор, и главный момент системы сил относительно любой точки в пространстве равны нулю. Так как главный вектор есть равнодействующая приведенной системы сходящихся сил, то условия их равновесия удовлетворяются выражениями (2.36). Равновесие системы пар, которой эквивалентен главный момент, удовлетворяется выражением (2.38).

Тогда, с учетом (2.43) и (2.45):

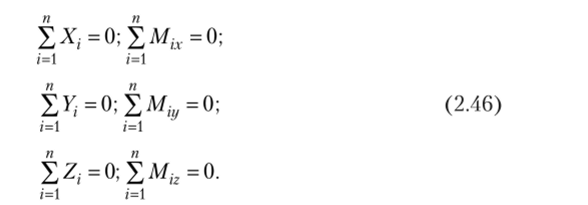
Уравнения (2.46) есть условия равновесия сил, произвольно расположенных в пространстве.

Система параллельных сил

Центр параллельных сил. Для пространственной системы параллельных сил координаты центра находят с помощью теоремы Вариньона (2.17) по методике, использованной в подпараграфе 2.3.4 для плоской системы параллельных сил, поворачивая силы так, чтобы они были параллельны одной из координатных осей.

Координаты центра параллельных сил вычисляются, но формулам.

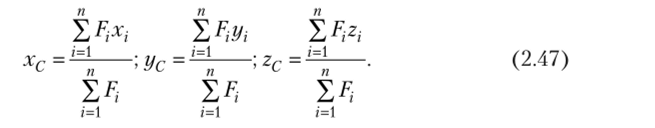
Уравнения равновесия пространственных сил. Если пространственную систему параллельных сил расположить параллельно одной из осей координат, например оси z, то легко убедиться, что часть уравнений равновесия (2.46) обращаются в тождества. При указанном расположении параллельных сил будут отсутствовать проекции сил на оси х и у (силы перпендикулярны плоскости хОу) и сумма моментов всех сил относительно оси z (силы параллельны этой оси).

Таким образом, для описания равновесного состояния системы параллельных сил в пространстве остаются только три уравнения равновесия: