Выбор основных систем метода сил.
Общая последовательность расчета

Для балочной фермы (рис. 13.16, а)> которая, так же как и предыдущая, является внутренне статически неопределимой (пс =1) из-за наличия избыточного стержня во второй панели фермы, основная системы может быть получена удалением одного из стержней именно в этой панели (рис. 13.16, б и в). Недопустимость удаления других стержней фермы показана на рис. 13.16, г, в результате чего вторая панель… Читать ещё >
Выбор основных систем метода сил. Общая последовательность расчета (реферат, курсовая, диплом, контрольная)
Как было отмечено в предыдущем параграфе, основной системой метода сил будем называть геометрически неизменяемую статически определимую систему, полученную из заданной статически неопределимой путем удаления избыточных связей.
При получении основной системы могут удаляться как внешние связи, так и внутренние, или их комбинации. Получение основной системы метода сил предполагает многовариантность, так как для любой статически неопределимой системы можно, в принципе, предложить сколь угодно много основных систем. Поэтому неизбежно встает вопрос о выборе основной системы с точки зрения ее рациональности для данной расчетной схемы и действующей на нее нагрузки.
Рациональность выбора предполагает следующие требования к основной системе.
- 1. Основная система должна быть проста для расчета.
- 2. Коэффициенты при неизвестных системы канонических уравнений метода сил и свободные члены, полученные на основе выбранной основной системы, должны быть, по возможности, одного порядка. Различие коэффициентов системы алгебраических уравнений на несколько порядков обычно приводит к ухудшению ее обусловленности и, как следствие, к ошибочным результатам расчета.
- 3. Выбранная основная система должна давать возможность получить как можно больше нулевых значений побочных коэффициентов при неизвестных и свободных членов системы уравнений. Это позволяет упростить решение этой системы и получить более точный результат.
Естественно, эти требования относятся, главным образом, к системе с большой степенью статической неопределимости. При пс < 3 наиболее важным является первое требование.
Рассмотрим несколько примеров выбора основных систем для плоских стержневых систем.
1. Для статически неопределимых одпопролетных балок (рис. 13.8 и 13.9) основная система может быть выбрана путем удаления линейных связей на одной из опор, т. е. основная система будет представлять собой консольную балку (рис. 13.8, в и 13.9, в), или удалением связей, препятствующих повороту в защемлениях (рис. 13.8, б и 13.9, б). Второй вариант предпочтительнее, так как в грузовом состоянии основной системы эпюры изгибающих моментов по концам балок будут иметь нулевые значения, что облегчает счет.
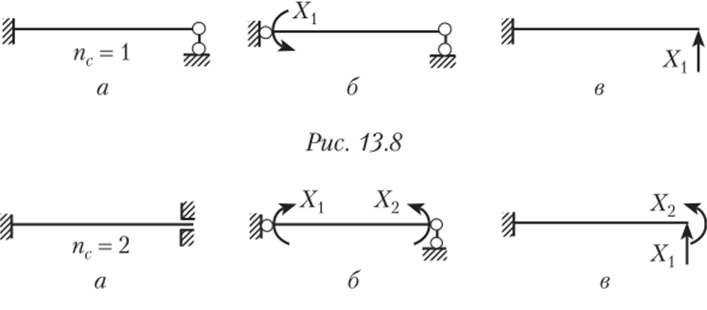
Рис. 13.9.
а б в
2. Для неразрезной балки (рис. 13.10, а) основная система может быть получена удалением промежуточных опор балки (рис. 13.10, б), удалением угловых связей (врезкой шарниров) над каждой промежуточной опорой (рис. 13.10, в) и комбинацией этих двух приемов (рис. 13.10, г). Рациональным для неразрезной балки является вариант, изображенный на рис. 13.10, в. В этом случае каждый пролет балки в основной системе работает как простая балка, независимо от других пролетов, что приводит к простым эпюрам изгибающих моментов и простоте вычисления как коэффициентов при неизвестных, так и свободных членов. Кроме того, при любом количестве неизвестных метода сил каждое из уравнений системы будет содержать не более трех неизвестных из-за равенства нулю побочных коэффициентов.
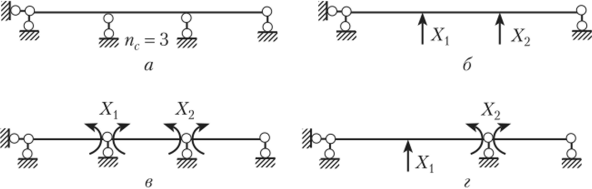
Рис. 13.10.
3. Для П-образной трижды статически неопределимой рамы (рис. 13.11, а) показаны шесть вариантов основной системы (рис. 13.11, б — ж), из которых наиболее рациональными являются основные системы, изображенные на рис. 13.11, е и ж. В первом случае основная система после удаления связей превращена в трехшарнирную раму, во втором — в балочную систему, в которой два стержня (левая стойка и ригель рамы) при отсутствии поперечных нагрузок будут нулевыми, а при их наличии будут работать как простые балки.
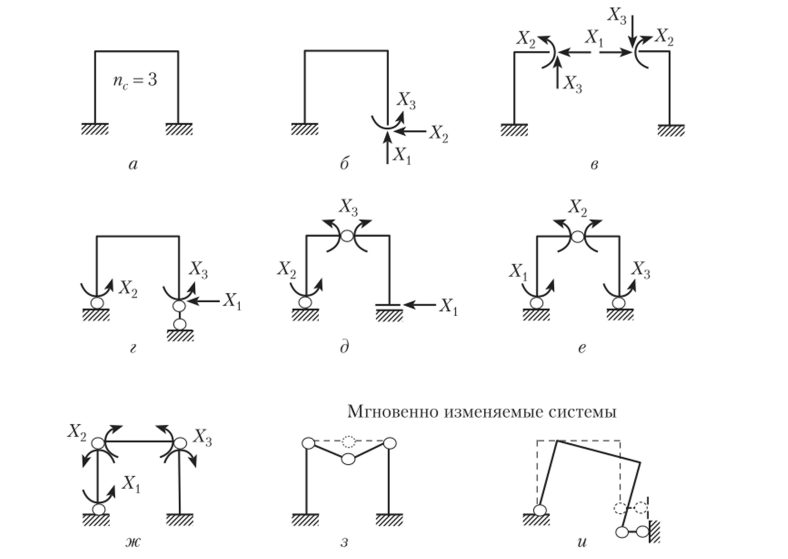
Рис. 13.11.
Основные системы, приведенные на рис. 13.11, з, гг, являются примерами неправильного удаления связей.
В основной системе, показанной на рис. 13.11, гг, удалены: угловая связь в правой опоре (получили шарнирно неподвижную опору), в правой опоре — угловая и вертикальная линейная связи. В результате оставшиеся линейные связи (две в левой опоре и одна горизонтальная в правой) имеют общую точку пересечения — мгновенный центр вращения, вокруг которого и произойдет бесконечно малый поворот расчетной схемы.
В основной системе, показанной на рис. 13.11, з, удалены три угловые связи в сечениях ригеля рамы, в результате чего врезанные шарниры оказались расположены на одной прямой.
4. Для двухпролетной одноэтажной рамы (рис. 13.12, а) показаны два возможных варианта основной системы (рис. 13.12, 6 и в) и изменяемая основная система (рис. 13.12, г), имеющая мгновенный центр вращения точку О.
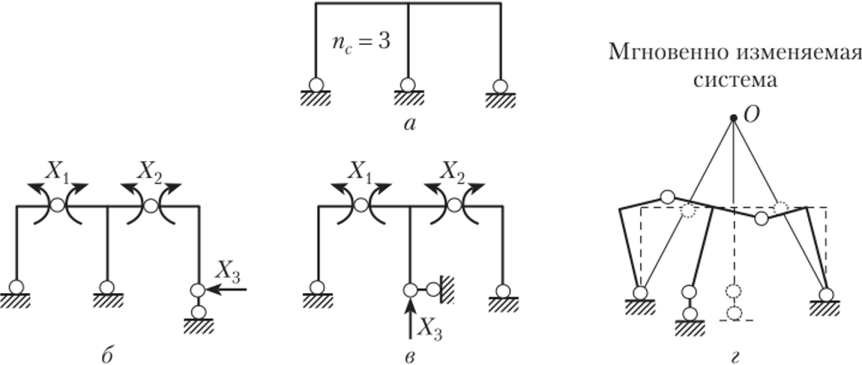
Рис. 13.12.
- 5. Для рамы с несмещающимися узлами (несвободной рамы) (рис. 13.13, а) показаны три варианта основной системы (рис. 13.13, б — г), из которых последняя является наиболее рациональной. Эта основная система получена врезкой сквозных шарниров во все узлы рамы, в результате чего заданная расчетная схема превращена в шарнирную (ферму), где каждый стержень работает как простая балка. На рис. 13.13, д показана основная система с неприемлемым вариантом удаления связей: в левом защемлении, кроме угловой связи, удалена горизонтальная линейная связь; в стойке удалена угловая связь в верхнем ее сечении, в результате чего вся стойка из-за наличия опорного шарнира стала представлять собой вертикальную линейную связь. В результате верхний диск (ригель) оказался прикрепленным к основанию тремя параллельными вертикальными связями, что недопустимо.
- 6. Для однопролетной рамы с затяжкой (рис. 13.14, а) основная система может быть получена:
- — удалением горизонтальной связи в одной из опор рамы и затяжки, в результате чего получается балка с осью ломаного очертания (рис. 13.14, в)
- — врезкой шарнира в ригеле и удалением затяжки, в результате основная система принимает вид трехшарнирной рамы (рис. 13.14, в)
- — удалением горизонтальной связи в одной из опор и врезкой шарнира в ригеле, результат — распорная рама с затяжкой (рис. 13.14, г).

Рис. 13.13
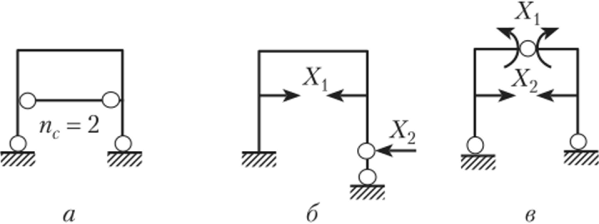
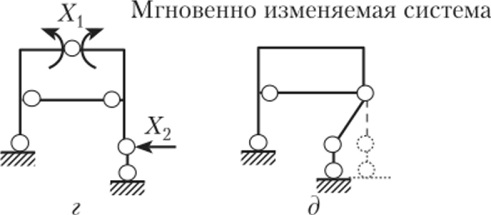
Рис. 13.14.
Недопустимый вариант показан на рис. 13.14, Э, где удалена горизонтальная линейная связь в правой опоре, а шарнир врезан в узел на уровне затяжки. В результате имеющийся в расчетной схеме замкнутый контур остался статически неопределимым (в контуре по его обходу всего два шарнира вместо необходимых трех), а стойка рамы ниже врезанного шарнира стала геометрически изменяемой частью схемы (три шарнира на одной прямой).
7. Для балочного замкнутого контура (рис. 13.15, а), расчетная схема которого имеет внутреннюю статическую неопределимость, основная система может быть получена удалением только внутренних связей (рис. 13.15, б — г). В случае удаления хотя бы одной внешней связи (рис. 13.15, д) схема превращается в механизм.
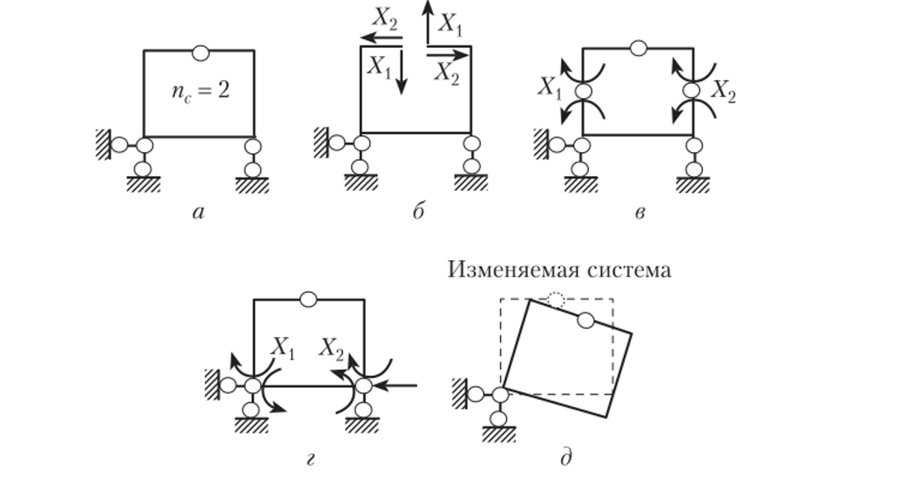
Рис. 13.15.
8. Для балочной фермы (рис. 13.16, а)> которая, так же как и предыдущая, является внутренне статически неопределимой (пс =1) из-за наличия избыточного стержня во второй панели фермы, основная системы может быть получена удалением одного из стержней именно в этой панели (рис. 13.16, б и в). Недопустимость удаления других стержней фермы показана на рис. 13.16, г, в результате чего вторая панель остается статически неопределимой частью расчетной схемы, а вся схема превращается в механизм.
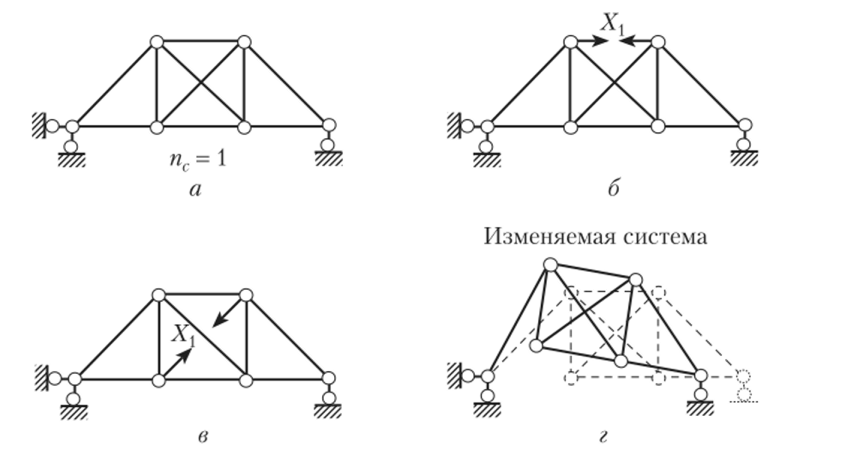
Рис. 13.16.
9. Для трехпролетной балочной фермы (рис. 13.17, а) основная система может быть получена как удалением промежуточных вертикальных опорных связей (рис. 13.17, б), так и удалением стержней фермы (рис. 13.17, в). Второй вариант предпочтительнее, так как в этом случае основная система представляет собой три отдельно работающие балочные фермы, и при загружении одной из них в стержнях двух других не будет возникать никаких усилий.

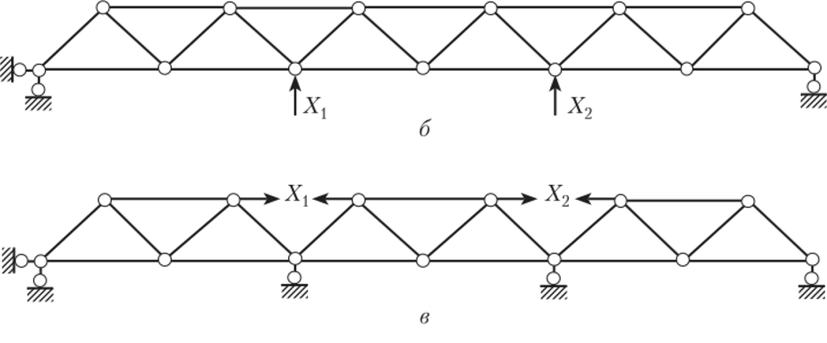
Рис. 13.17.
Приведенные выше примеры не исчерпывают всего многообразия приемов при выборе основных систем метода сил для различных статически неопределимых расчетных схем, они лишь дают представления, каким образом могут быть удалены избыточные связи и как получить наиболее рациональную основную систему.
Общая последовательность расчета методом сил приведена в табл. 13.1.
Таблица 13.1
Последовательность расчета методом сил.
№ п/п. | Балки и рамы. | Комбинированные системы. | Фермы. |
Определить степень статической неопределимости. | |||
пс = ЗК — Ш. | пс = ЗК — Ш. | пс = С — 2У. | |
Записать систему канонических уравнений в общем виде. | |||
Выбрать основную систему метода сил. | |||
Построить эпюры усилий в основной системе от последовательного приложения единичных сил по направлению удаленных связей. | |||
Mf (при i=l,…, п) | Mf, Nf (при i = 1,…, п) | Nf (при i=l,…, п). | |
Окончание табл. 13.1
№ п/п. | Балки и рамы. | Комбинированные системы. | Фермы. |
Построить эпюры усилий в основной системе от заданной нагрузки. | |||
m°f | М% NnF | ||
Определить коэффициенты при неизвестных системы канонических уравнений. | |||
А/РЛ/Р. 5й = 1Р#-ск. т El | V/Q, V/P дгРдгр 8/* = SJ ' dx+2 ' * /. * El ct ЕЛ | N9N? Сф. | |
Определить свободные члены системы канонических уравнений. | |||
Л v, MfMf: V = S1 ' dv m El | . v f M?M°F , v n? nqf. Л" = 5( El | id''. | |
Записать систему канонических уравнений и из се решения определить значения неизвестных X, | |||
Построить эпюры усилий в заданной расчетной схеме. | |||
MF = 'ZMfxi+M°F— NF = '?N?Xi + №F | |||
Произвести деформационную проверку расчета. | |||
р/ т El либо. IIя;" ' л-«. т Е1 где А?" = ХЛ/Р. | 2/*?" ' d*+ I'^/.o m El Сф EA либо. ш] El 4. где. М° = ЪМ р ; Я0 = Е*? | X /=(),. ct ?4. либо. iV°iVr. Y /_о Сф ЕЛ где. | |
Расчет окончен. | |||
Определить на основании дифференциальной л АМ зависимости Q = —-— поперечные силы на всех ад; участках расчетной схемы и построить эпюру QF | |||
Из условий равновесия узлов определить продольные силы во всех стержнях и построить эпюру NF | |||
Произвести статические проверки равновесия: при правильно произведенном расчете любая отсеченная часть схемы или вся схема, отсеченная от опор, под действием внутренних и внешних сил должна удовлетворять условиям равновесия. | |||
Расчет окончен. | |||
Примечание: т — число участков интегрирования при изгибе; Сф — число стержней фермы.
Как видно из табл. 13.1, общая последовательность расчета не зависит от типа расчетной схемы. Различия появляются лишь при определении коэффициентов при неизвестных и свободных членов по формуле Максвелла — Мора.
При выполнении расчета необходимо обратить внимание на следующие пункты табл. 13.1.
- 1. Выполнение деформационной проверки расчета (см. п. 10 табл. 13.1). Смысл деформационной проверки такой же, как и у системы канонических уравнений: она отрицает перемещения в заданной расчетной схеме по направлению удаленных связей. Для большей корректности деформационной проверки желательно выбрать новую основную систему метода сил и построить в ней эпюры усилий от единичных сил, приложенных по направлениям удаленных связей Mf, Nf, и их суммарные эпюры Mf, Nf. В связи с этим деформационные проверки могут быть локальными (использование эпюр Mf, Nf) или общими (использование эпюр Mf, Nf). Оценка погрешности расчета производится по сравнению сумм положительных и отрицательных величин вычисленных интегралов и не должна превышать 1%.
- 2. Построение эпюры поперечных сил (см. п. 11 табл. 13.1). Определение поперечных сил на участках с прямолинейной эпюрой изгибающих моментов (рис. 13.18) производят на основании правил, изложенных в параграфе 10.2 (см. рис. 10.11). Для горизонтально ориентированного стержня при выполнении принятого ранее правила знаков для изгибающих моментов (см. рис. 10.4) можем записать
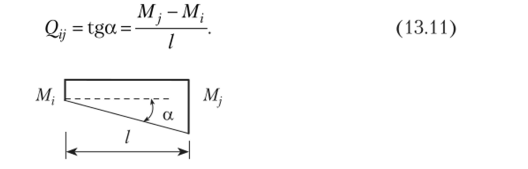
Рис. 13.18
Для участков, где действует равномерно распределенная нагрузка, фигуру эпюры изгибающих моментов можно разложить на две составляющие (рис. 13.19): прямолинейную и «балочную», и для каждой из них построить эпюры поперечных сил, а результаты сложить. В силу того, что на рассматриваемом участке эпюра поперечных сил должна быть прямолинейной, ординаты эпюры поперечных сил по концам участка можно записать как
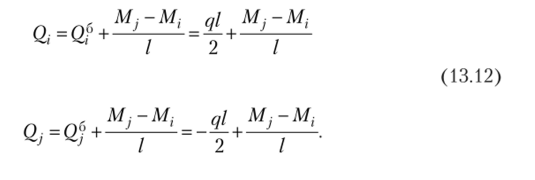
и.
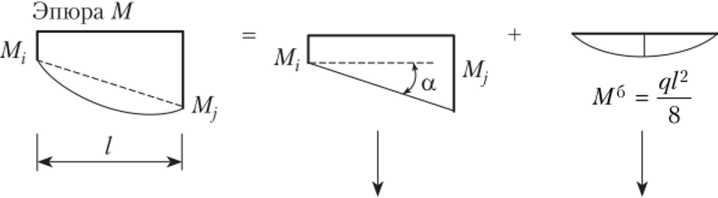
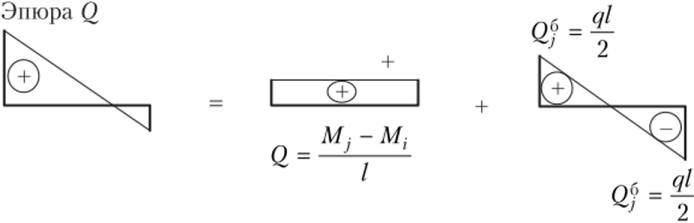
Рис. 13.19.
Для вертикальных и наклонных стержней расчетной схемы «верх» и «низ» рассматриваемого участка выбираются произвольно.
Рассмотрим несколько примеров расчета статически неопределимых систем методом сил при действии внешней нагрузки.
Пример 13.1.
Требуется рассчитать неразрезную балку, показанную на рис. 13.20, а.
Решение. 1. Степень статической неопределимости при К = 2, Ш = 4ис = 3*2−4 = 2.
- 2. Система канонических уравнений:
- 5j |Xj + 512Х2 + А|/г = 0;
- 62i^iг 622Х2 «Г Д2^г — 0.
- 3. Выбранная основная система показана на рис. 13.20, 6.
- 4. Определим усилия в основной системе от единичных моментов, последовательно прикладываемых по направлению удаленных связей (рис. 13.20, в и г), т. е. построим эпюры М® и М2. Кроме этого, воспользуемся простотой задачи и построим деформированные схемы основной системы от единичных воздействий, на которых покажем возможные перемещения, представляющие собой коэффициенты при неизвестных канонических уравнений.
- 5. Определим усилия в основной системе от действия заданной нагрузки и построим эпюру М(1- (рис. 13.20, д). Здесь также покажем перемещения по направлению удаленных связей, представляющие собой свободные члены канонических уравнений.
- 6. Определяем коэффициенты при неизвестных канонических уравнений:
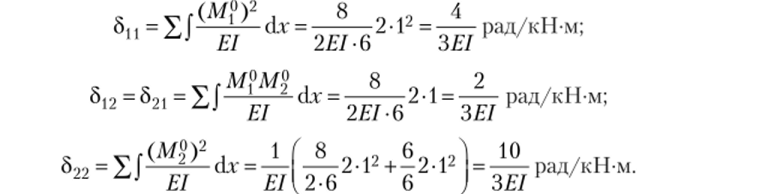
7. Определим свободные члены канонических уравнений:
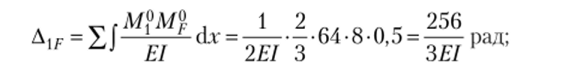

Рис. 13.20.
8. Решим систему канонических уравнений:
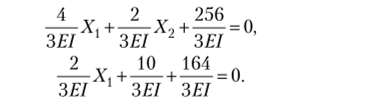
Упростим полученную систему уравнений, умножив все его члены на 1,5ЕГ. 2Х, +Х2+ 128 = О, Х{ + 5Х2 + 82 = 0.
Используя правило Крамера, получим.
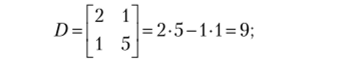
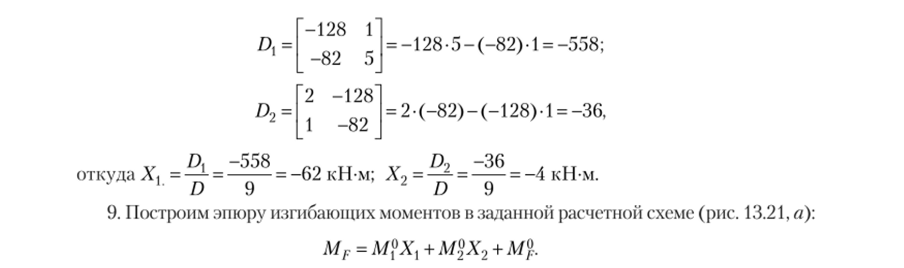
Для неразрезных балок указанное сложение производится достаточно просто: необходимо отложить на опорах найденные значения неизвестных и к полученной эпюре опорных изгибающих моментов «подвесить» эпюру М{?.
10. Выполним деформационную проверку расчета. Для этого выбираем новую основную систему (рис. 13.21, б), в которой прикладываем сразу все единичные силы по направлению удаленных линейных связей и от их действия строим эпюру AfJ. Сравнивая полученную эпюру М® с эпюрами М] и М$, использованными в расчете, видим, что она им не подобна, т. е. производимая проверка будет достаточно корректна.
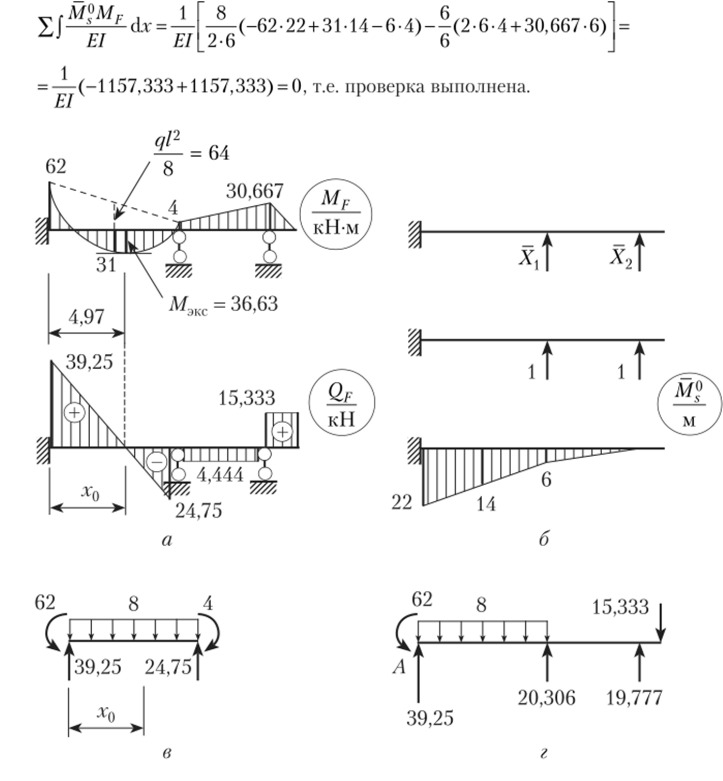
Рис. 13.21.
11. Выполним построение эпюры QF на основании дифференциальной зависимо- п сШ
сти Q = —— по участкам расчетной схемы. ах
Участок 1 — левый пролет балки. Пролет загружен равномерно распределенной нагрузкой, поэтому для нахождения значений поперечных сил по концам участка используем прием, приведенный на рис. 13.19 и описанный формулой (13.12):
(2лев=М+~4~(~62) =39,25 кН;
^28.
QH РАВ = _М + ~4— (~62) = -24,75 кН.
^ 2 8.
Участок 2 — правый пролет балки. Нагрузка в пролете отсутствует, эпюра изгибающих моментов очерчена по наклонной прямой. Следовательно, поперечная сила по всему пролету постоянна. Ее значение вычисляем по формуле (13.11): -30.667-М).
Участок 3 — консоль балки. Поперечная сила Q = ЦРф:ш = 15,333 кН.
Построенная по полученным значениям эпюра QF показана на рис. 13.21, а.
В левом пролете эпюра QF имеет нулевое значение на расстоянии х{) от левой опоры. Найдем экстремальное значение изгибающего момента в этом сечении (рис. 13.21, в):
?>о = 2>ев = 39,25 — 8 • х0 = 0, х0 = 4,97 м.
Мэкс = Еа/лев = 39,25? 4,97 — 8 • 4,97 • 0,5? 4,97 = 36,63 кН м.
12. Произведем статические проверки расчета, для чего из равновесия опорных узлов по построенным эпюрам MFи QFопределим опорные реакции (рис. 13.21, г).
Для отсеченной от опор балки составляем уравнения равновесия:
2> = 39,25 + 20,36 + 19,777 — 8 • 8 — 15,333 = 79,333 — 79,333 = 0;
ЪМЛ = - 62 — 20,306 • 8 — 19,777 • 14 + 15,333 • 16 + 8 • 8 • 4 = -501,326 + 501,328 = 0.
Таким образом, проверки равновесия также выполняются. Следовательно, расчет неразрезной балки произведен правильно.
Требуется рассчитать раму, показанную на рис. 13.22, а.
Решение. 1. Степень статической неопределимости при К = 2, Ш = 4 пс = 3 • 2 — 4 = 2.
2. Система канонических уравнений имеет вид.
ЪХ{ + 6|22 + A j/r = 0;
- 621Х, + $ 222 + &2 °F = 0-
- 3. Основная система показана на рис. 13.22, б. Выбрана она путем «врезки» двух шарниров в средний узел рамы. При этом реакция в удаленной угловой связи между стойкой и ригелем рамы Х2 может быть отнесена как в левое, так и в правое от узла сечение ригеля.
- 4. Определим усилия в основной системе от единичных моментов, последовательно прикладываемых по направлению удаленных связей (рис. 13.22, в и г), для чего определим реакции от указанных воздействий и построим эпюры М$ и М?.
- 5. Определим усилия в основной системе от действия заданной нагрузки и построим эпюру А/? (рис. 13.22, д).
- 6. Определим коэффициенты при неизвестных:
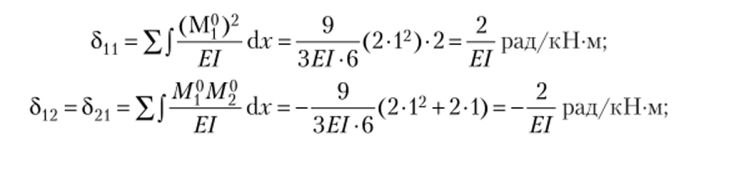
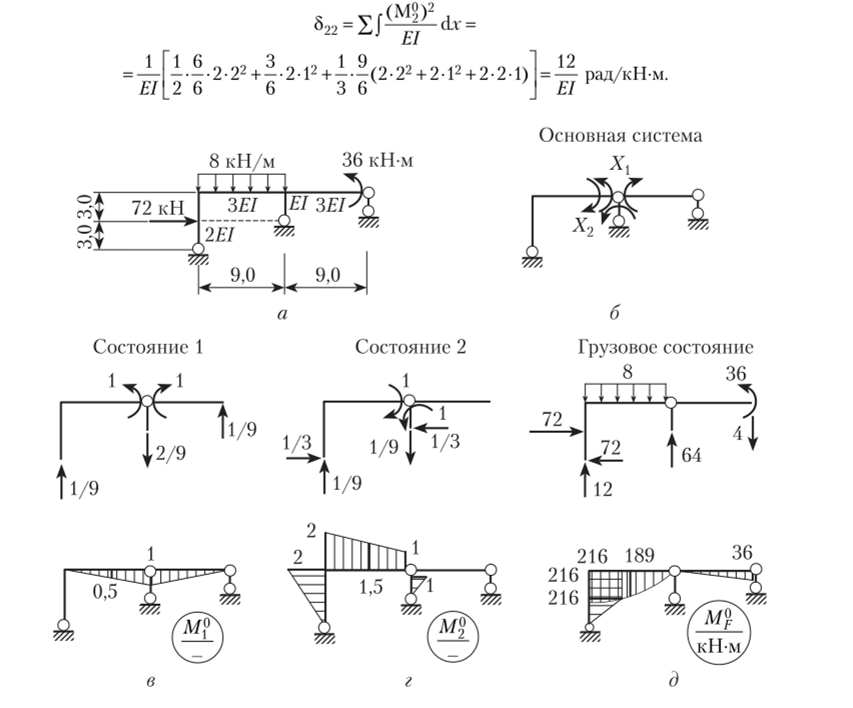
Рис. 13.22
7. Определим свободные члены канонических уравнений:

8. Решим систему канонических уравнений:
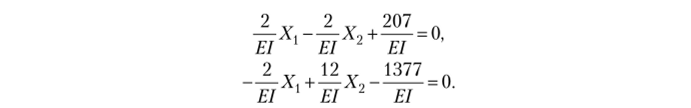
Упростим полученную систему уравнений, умножив все члены на 0,5?7: X, — Х2 + 103,5 = 0, -X, + 6Х2 — 688,5 = 0.
Используя правило Крамера, получим.
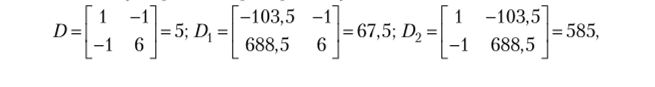
Усилия от действительных значений реакций в удаленных связях и результат сложения (эпюра MF) показаны на рис. 13.23, а.
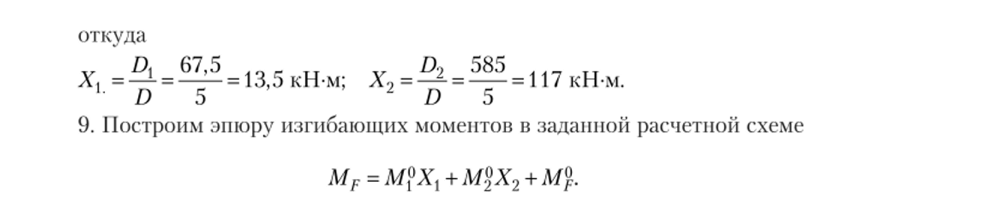
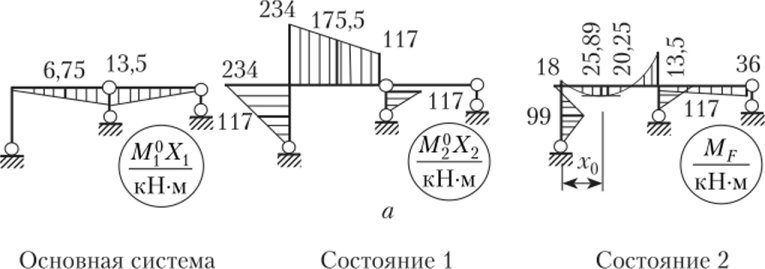
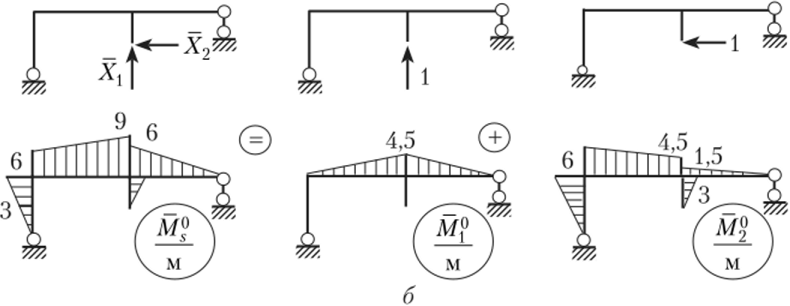
Рис. 13.23.
10. Произведем деформационную проверку расчета, для чего выберем новую основную систему (рис. 13.23, б), для которой построим эпюры М{ и их сумму, эпюруМСравнивая полученную эпюру М® с эпюрами Л/,° и М§, использованными в расчете, видим, что она им не подобна, т. е. производимая проверка будет достаточно корректна.
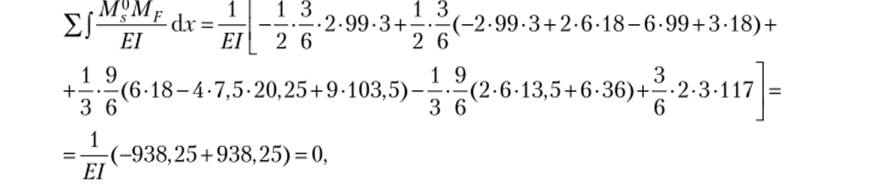
т.е. проверка выполнена.
11. Построим эпюру Q,: на основании дифференциальной зависимости Q = ——.
ах
по участкам расчетной схемы (рис. 13.24, а).
Участки Л— К и К — D. Используя формулу (13.11), получим.
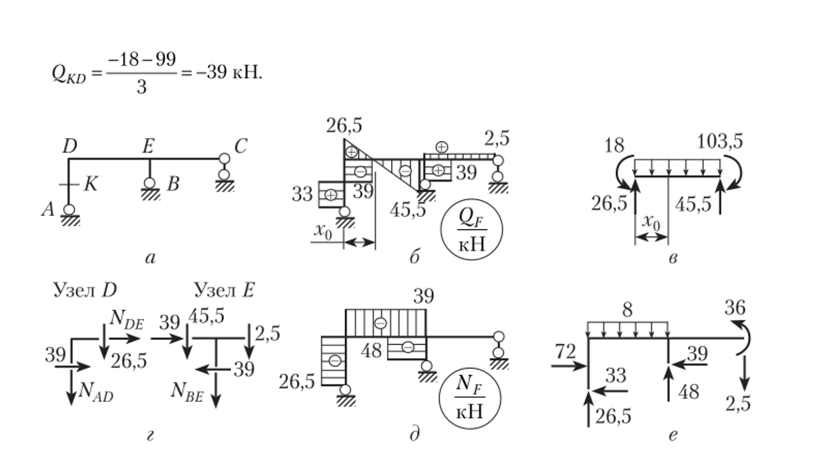
Рис. 13.24.

Построенная по полученным значениям эпюра QF показана на рис. 13.24, 6.
В левом пролете эпюра QF имеет нулевое значение на расстоянии л;0 от левой опоры. Вырежем ригель рамы в левом пролете рамы (рис. 13.24, в) и найдем экстремальное значение изгибающего момента в этом сечении.
Qo = 1>ЕВ = 26,5 — 8 • х0 = 0, *0= 3,31 м.
Мжс = Ел/лев = 26,5 • 3,31- 8 • 3,31 0,5 — 3,31 = 25,89 кН м.
- 12. Определим продольные силы в стержнях рамы и построим эпюру NF, для чего поочередно вырежем узлы D и Е рамы (рис. 13.24, г) и из их равновесия найдем продольные силы NAD, Nde и Nbe. Построенная по полученным значениям эпюра показана на рис. 13.24, д.
- 13. Произведем статические проверки расчета, для чего из равновесия опорных узлов по построенным эпюрам NF и QF определим опорные реакции (рис. 13.24, ё).
Для отсеченной от опор рамы составим уравнения равновесия:
ZY= 26,5 + 48 + 19,777 — 8 • 9 — 2,5 = 74,5 — 74,5 = 0;
Их = 72 — 39 -33 — 8? 9 — 2,5 = 72 — 72 = 0;
ИМЛ = 72? 3 + 8 • 9 • 4,5 — 48 • 9 — 39 • 3 + 2,5? 18 — 36 = -585 + 585 = 0.
Таким образом, проверки равновесия также выполняются. Следовательно, расчет рамы произведен правильно.
Пример 13.3.
Требуется построить эпюру изгибающих моментов в ригеле и определить продольные силы в стойке и подкосе комбинированной расчетной схемы, показанной на рис. 13.25, а при соотношении жесткостей ЕЛ / ЕЛ = 15 м 2.
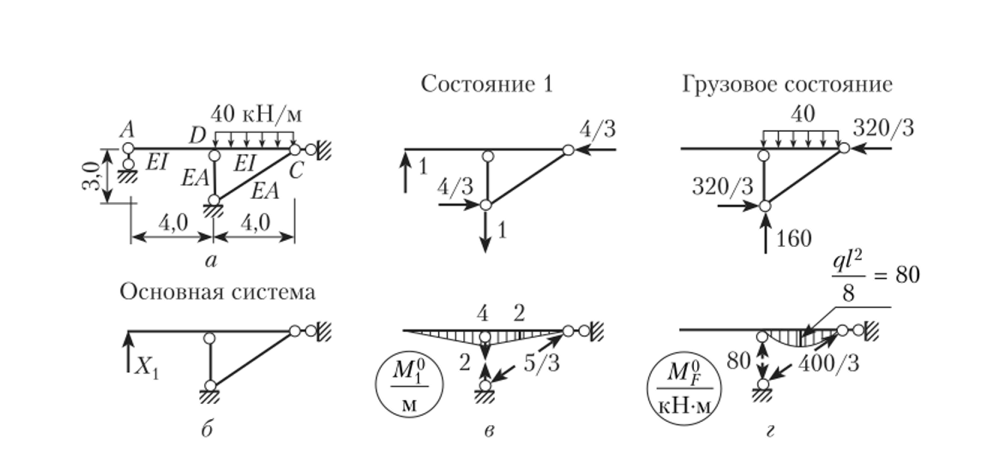
Рис. 1325.
Решение. 1. Расчетная схема имеет число контуров К = 3. Число простых шарниров (или связей, недостающих до полного защемления) определяем по узлам расчетной схемы.
Узел Л: Ш = 2.
Узел В: III = 2 (два примыкающих к основанию шарнира).
Узел С: III = 3 (в опорной линейной связи недостает до полного защемления двух связей, и один шарнир соединяет стержни расчетной схемы).
Узел D: Ш = 1 (один примыкающий шарнир между двумя стержнями схемы).
Итого III = 8.
Степень статической неопределимости при К = 3, Ш = 8/?с = 3 3−8=1.
- 2. Каноническое уравнение имеет вид + Alf— 0.
- 3. Выбранная основная система показана на рис. 13.25, 6.
- 4. Определим усилия в основной системе от единичной силы, приложенной по направлению удаленной связи, для чего определим реакции от указанного воздействия и построим эпюры А/p и iVj0 (рис. 13.25, в).
Так как в рассматриваемой расчетной схеме продольные усилия в ригеле отсутствуют, продольные силы в стойке и подкосе здесь и далее будем показывать (для упрощения графического материала) непосредственно на эпюрах изгибающих моментов.
- 5. Определим усилия в основной системе от действия заданной нагрузки и построим эпюру (рис. 13.25, г).
- 6. Определим коэффициент при неизвестном канонического уравнения:

8. Определим неизвестное канонического уравнения:
X, = -А1Р/6″ = -468,741 / 44,393 = -10,559 кН.
9. Построим эпюру изгибающих моментов в заданной расчетной схеме и определим продольные силы в стойке и подкосе:
MF = MfXt + M°F; NF = N*X{ + №F.
Результаты построения показаны на эпюре MF (рис. 13.26, а).
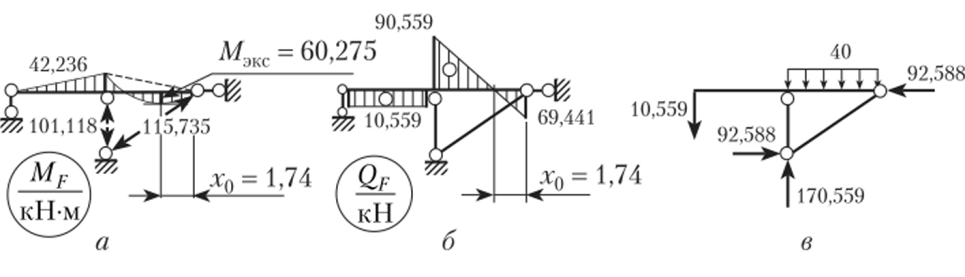
Рис. 13.26.
Построение эпюры Qr (рис. 13.26, а) выполняется так же, как и в предыдущих примерах.
10. Для выполнения статических проверок расчета определим реакции в опорных связях на основании принципа независимости действия сил.
Ra=X{= -10,559 кН.
Rc = R*xXx + R$f = 320 / 3 + (4 / 3) • (-10,559) = 92,588 кН.
VB = Vj>xXx + VgF = 160 + (-1) • (-10,559) = 170,559 кН.
IIв = H°mX{ + H%F = 320 / 3 + (4 / 3) • (-10,559) = 92,588 кН.
Для отсеченной от опор комбинированной расчетной схемы составим уравнения равновесия:
LУ= 170,559 — 10,559 — 40 • 4 = 0;
1х= 92,588 — 92,588 = 0;
ZMB = 40 • 4? 2 — 10,559 • 4 — 92,588? 3 = 320 — 320 = 0.
Таким образом, проверки равновесия также выполняются. Следовательно, расчет произведен правильно.
Пример 13.4.
Требуется определить усилия в консольной ферме (рис. 13.27, а) при следующих соотношениях жесткостей стержней: ЕЛЗС = ЕА; пояса — 2ЕЛ; раскосы — 1,25?Л; стойки — ЕЛ.
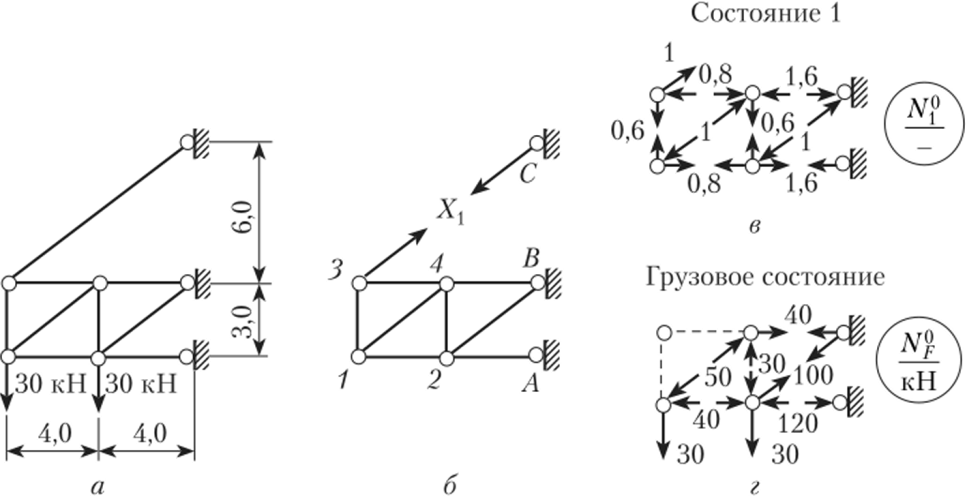
Рис. 13.27.
Решение. 1. Степень статической неопределимости фермы при У = 7, Сф = 9, С()п = б яс = С — 2У = (9 + 6) — 2 • 7 = 1.
2. Каноническое уравнение.
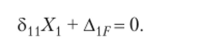
- 3. Выбранная основная система показана на рис. 13.27, б.
- 4. Определим усилия в основной системе от единичной силы, приложенной, но направлению удаленной связи, и построим эпюру N,0 (рис. 13.27, в).
Определение усилий в ферме производим любым удобным способом — вырезания узлов или сечений.
5. Определим усилия в основной системе от заданной нагрузки и построим эпюру №f (рис. 13.27, г).
Дальнейший ход расчета, включающий в себя определение коэффициента при неизвестном, свободного члена, решение канонического уравнения и определение усилий в заданной схеме фермы (NF =N^X{ + JV?), приведен в табл. 13.2.
Таблица 13.2
Определение усилий в статически неопределимой ферме (к примеру 13.4).
Номер стержня. | /, м. | 0 = ^ ЕА | Nf | №Р, кН. | N?l Р. | (IV,0)2/. р | N°N°Fl Р. | nf, кН. | |
1−2. | 0,8. | — 40. | 1,6. | 1,28. | — 64. | 28,4. | — 11,6. | ||
2−3. | 1,6. | — 120. | 3,2. | 5,12. | — 324. | 56,8. | — 63,2. | ||
3−4. | — 0,8. | — 1,6. | 1,28. | — 28,4. | — 28,4. | ||||
А-В | — i, 6. | — 3,2. | 5,12. | — 128. | — 56,8. | — 16,8. | |||
1−3. | 0,6. | 1,8. | 1,08. | 21,3. | 21,3. | ||||
2−4. | 0,6. | — 30. | 1,8. | 1,08. | — 54. | 21,3. | — 8,7. | ||
1−4. | 1,25. | — 1. | — 4. | — 200. | — 35,5. | 14,5. | |||
2-В | 1,25. | — 1. | — 4. | — 400. | — 35,5. | 64,5. | |||
3-С | 35,5. | 35,5. | |||||||
I = 32,96. | I =-1170. | ||||||||
Откуда: ЕА6п = 32,96; EAA{F = -1170,.
Х,= -ЕААр/ЕАЬп = - (-1170) / 32,96 = 35,4976 * 35,5 кН.