Учет симметрии в задачах динамики

В симметричных расчетных схемах с симметрично расположенными одинаковыми массами на основании свойств симметрии возможны упрощения как при определении частот свободных колебаний, так и при определении усилий от вибрационной нагрузки.

Для симметричных расчетных схем с симметрично расположенными массами возможно разложение форм колебаний на симметричные и кососиммегричные, при которых силы инерции также будут либо симметричными, либо кососимметричными.

Упрощение достигается за счет разделения уравнения частот (15.41) при наличии осей симметрии на уравнения меньших порядков. Так, если расчетная схема имеет одну ось симметрии, уравнение частот разделяется на два уравнения; если расчетная схема имеет две оси симметрии — на четыре. При этом сумма порядков уравнений остается равной порядку исходного уравнения. Разделения уравнения частот (15.41) можно достичь двумя путями: либо использованием групповых перемещений, либо представлением расчетной схемы в виде ее симметричной части.

Рассмотрим расчетную схему с тремя степенями свободы масс (рис. 15.26, а), имеющую одну ось симметрии. В этой расчетной схеме три формы колебаний можно представить как две симметричные (рис. 15.26, б, в) и одну кососимметричную (рис. 15.26, г). В этом случае для симметрично расположенных масс величины податливостей определяются от групповых единичных сил (см. рис. 15.27, в, г). При этом побочные податливости, связывающие симметричные и кососимметричные силы инерции, обращаются в ноль. Это и приводит к распаду уравнения частот на две независимые группы уравнений, из которых одна позволяет определить частоты симметричных свободных колебаний, а другая — кососимметричных.

Приведенные на рис. 15.26 формы колебаний на основании свойств симметрии (см. параграф 13.5) позволяют назначить на оси симметрии граничные условия при рассмотрении половины расчетной схемы.

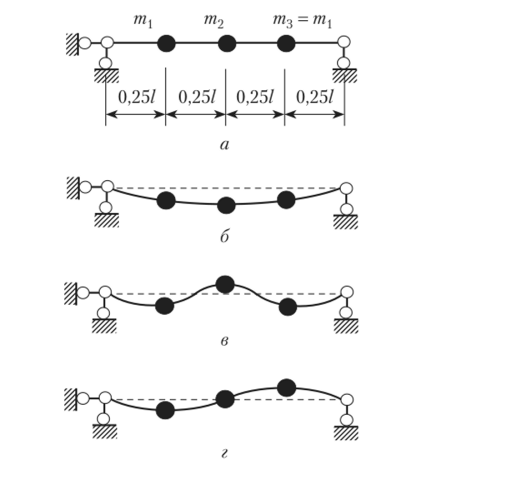
Рис. 15.26.

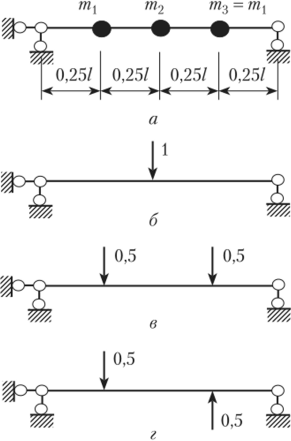
Рис. 15.27.

На рис. 15.28, а изображена половина расчетной схемы для симметричных колебаний (см. рис. 15.27, б, в). В силу свойства 1 (см. параграф 13.5) на оси симметрии должен отсутствовать угол поворота, но сечение способно перемещаться по вертикали. Этим условиям соответствует подвижное в вертикальном направлении защемление. Следовательно, для данной расчетной схемы степень свободы масс будет равна W_m = 2, и уравнение частот будет второго порядка. Так как масса т₂ расположена непосредственно на оси симметрии и принадлежит одновременно и правой, и левой частям схемы, здесь она учитывается в половину своей величины.

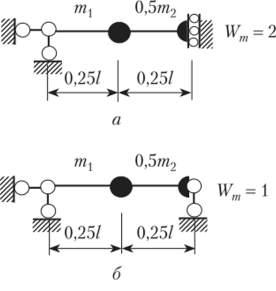
Рис. 15.28 418

На рис. 15.28, б изображена половина расчетной схемы для кососимметричных колебаний (см. рис. 15.27, г). В силу свойства 2 (см. параграф 13.5) на оси симметрии должно отсутствовать вертикальное перемещение сечения, но разрешен его свободный поворот. Этим условиям соответствует постановка вертикальной шарнирно подвижной опоры. Следовательно, для полученной расчетной схемы степень свободы W_m = 1, и уравнение частот будет первого порядка. Общее число степеней свободы равно трем, но вместо определителя третьего порядка составляются два определителя — второго и первого порядков. Вычисление этих двух определителей существенно легче и короче, чем вычисление определителя третьего порядка.

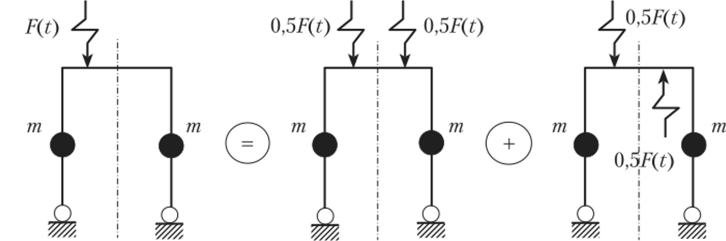
Рис. 15.29.

При действии вибрационной нагрузки последняя, как и при статических расчетах, раскладывается на симметричную и кососимметричную (рис. 15.29).