Устойчивость. 
Динамика и устойчивость сооружений

ВВЕДЕНИЕ

У.1. Понятие о потере устойчивости и критической нагрузке

29 августа 1907 г. за четверть часа до окончания рабочего дня в Канаде произошла трагедия — обрушился Квебекский мост, строившийся через реку Святого Лаврентия. С громоподобным треском рухнули девять тысяч тонн стальных конструкций вместе с кранами и рабочими. Погибли 74 человека. За считанные секунды огромный мост превратился в кучу жалких обломков, затонувших в реке. Мост представлял собой консольную ферму, которая наращивалась от опоры в сторону реки. Выпучивание отдельных стержней нижнего пояса было замечено еще за 23 дня до обрушения. Но на это никто не обратил внимания, так как нс знали причины возникновения прогибов. Катастрофа произошла вследствие «классической» потери устойчивости сжатых элементов моста. Таких примеров было несколько¹.

Например, 29 декабря 1896 г. обрушился мост у г. Аштабьюла (США) во время прохода поезда. Вместе с мостом упало 11 вагонов. Погибло 92 человека. Причина обрушения: потеря устойчивости сжатых составных элементов — раскосов и верхнего пояса (рис. У.1). Раскосы были соединены только по концам, в промежутке связей не было, т. е. каждый элемент работал отдельно, что существенно понижало их несущую способность. Интересно отметить, что фактические напряжения в раскосах были равны 4200 Н/см², а по формуле Эйлера критическое напряжение получается равным 195 Н/см². Мост простоял 10 лет. Приходится удивляться не тому, что он обрушился, а тому, почему он не обрушился раньше.

После ряда аварий инженерная мысль была направлена на выявление их причин. Оказалось, что установление того факта, что напряжения в материале конструкции не превосходят нормативной величины, еще не позволяет сделать заключение о надежности конструкции. Прежде всего такое заключение относится к сооружениям, имеющим сжатые и сжато-изогнутые стержни. В таких сооружениях возможно явление потери устойчивости даже в пределах упругой работы материала.

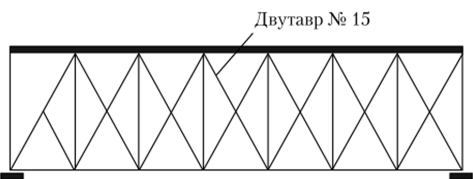
Рис. У.1. Фасад пролета моста.

¹Дмитриев Ф.Д. Крушение инженерных сооружений. М.: Госстройиздат, 1953.

Сущность явления потери устойчивости можно продемонстрировать на примере упругого идеально прямого консольного стержня, к концу которого в центре сечения приложена сосредоточенная сила, направленная вдоль оси стержня (рис. У.2, а). Пока величина силы не превосходит некоторого предельного значения, стержень в результате центрального сжатия будет только укорачиваться, сохраняя прямолинейную форму равновесия. Если при этом вывести его из состояния равновесия, приложив действующую кратковременно горизонтальную силу, то он, поколебавшись, займет первоначальное положение (см. рис. У.2, а). Таким образом, если стержень или любая конструкция, выведенная из состояния равновесия, вновь возвращается в свое первоначальное положение, то такое состояние считается устойчивым.

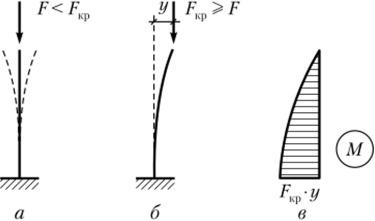
Рис. У.2. Демонстрация явления потери устойчивости При определенном значении силы, обозначаемом через Е_1ф и называемом критическим, выведенный из состояния равновесия стержень уже не возвращается в исходное положение (рис. У.2, б). Такое состояние системы уже будет неустойчивым. При F= F_Kp происходит разветвление форм равновесия, так называемая бифуркация. Это означает, что одной и той же нагрузке могут соответствовать другие формы равновесия, или деформированного состояния. Такого явления при решении задач прочности не встречалось.

Итак, критической силой, или нагрузкой, для всего сооружения либо для отдельного стержня называется то ее предельное значение, при котором начальная форма равновесия перестает быть устойчивой.

Граница между устойчивым и неустойчивым состояниями системы называется безразличным состоянием. В безразличном состоянии сжатый стержень обладает удивительным свойством. Он как бы теряет жесткость. Достаточно небольшого усилия, чтобы изменить его деформированную форму. Естественно, задаваемые перемещения весьма малы, но конечны и видимы простым глазом.

Изложенное выше явление потери устойчивости с появлением смежных форм равновесия предложено Эйлером. Однако его предложение не является всеобъемлющим. При расчете гибких конструкций типа стальных оболочек часто имеет место потеря устойчивости в виде «хлопка», когда система принимает форму равновесия, далекую от смежной. Этот факт подтверждается диаграммой «нагрузка — прогиб» (рис. У. З, а).

Существует еще понятие — потеря устойчивости в «малом» и «большом» (рис. У. З, б). При малых отклонениях шарика состояние будет устойчивым, а при больших отклонениях шарик выйдет из лунки и его состояние будет уже неустойчивым. Он потеряет устойчивость в «большом». Следует также иметь в виду, что в ряде случаев, особенно при расчете сложных многоэле;

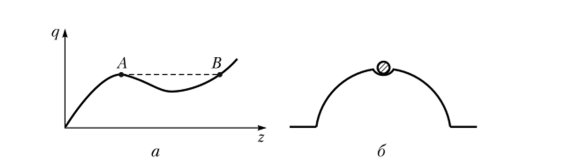
Рис. УЗ. Перескок состояния из Л в В (а) и демонстрация понятия о потере устойчивости в «малом» и «большом» (б) ментных конструкций, до общей потери устойчивости конструкции могут иметь место местные потери устойчивости отдельных элементов. Имеют место и другие виды потери устойчивости, не рассматриваемые в этой книге.

Обычный статический расчет, как правило, ведется по недеформированной схеме, т. е. по первоначальной геометрической схеме без учета величин прогибов стержней под нагрузкой. Особенность решения задач устойчивости состоит в том, что расчет сооружения производится с учетом его деформированной схемы. При потере устойчивости в стержнях, кроме продольных сил, появляются изгибающие моменты вследствие изгиба стержней. Чтобы подчеркнуть, что причиной изгиба является не поперечная нагрузка, а продольная сила, такой изгиб обычно называют продольным. На рис. У.2, в показана эпюра изгибающих моментов в стержне, изображенном на рис. У.2, 6. Эпюра в этом случае уже нелинейная.

Первые попытки решения вопроса о сопротивлении сжатых стоек принадлежат Леонардо да Винчи (1490 г.). Однако он получил неверные результаты. Экспериментально факт, что сопротивление сжатых стоек одинакового сечения обратно пропорционально квадратам их длины, был доказан в 1729 г. П. Мусхенбруком.

Первые теоретические исследования по вопросам устойчивости сжатых упругих стержней были выполнены Л. Эйлером в 1744 г. Однако в течение 100 лет эти исследования считались причудами великого математика. Дело в том, что основным материалом для сжатых колонн в то время служил камень или, что гораздо реже, чугун. При таком материале не может быть и речи о потере устойчивости в пределах упругости материала, т. е. для случаев, рассмотренных Л. Эйлером.

Вопросы расчета сооружений на устойчивость встали со всей полнотой только после появления нового строительного материала (стали) и в связи со строительством крупных инженерных сооружений, особенно после ряда крушений мостов из-за потери устойчивости сжатых элементов. Особенно активно наука об устойчивости различных конструкций развивалась в конце XIX и начале XX в. Здесь назовем лишь несколько широко известных среди строителей имен: Ф. С. Ясинский, С. П. Тимошенко, Б. Г. Галёркин, А. Н. Динник, В. 3. Власов, А. Ф. Смирнов и др.

В рамках настоящей книги рассматриваются стержневые системы, пластинки и оболочки в которых, как у Л. Эйлера, при нагружении напряжения не превосходят предела упругости.

Необходимо отметить, что в случае потери устойчивости зависимость между силами и перемещениями становится нелинейной^[1] (рис. У.4), поэто;

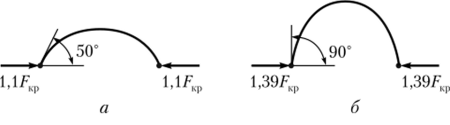
Рис. У.4. Доказательство нелинейности задач устойчивости му принцип независимости действия сил к задачам устойчивости уже неприменим.

В инженерной практике обычно различают два рода потери устойчивости форм равновесия. Вообще, такой подход не исчерпывает и не характеризует полностью специфику поведения различных конструкций. Но в приложении к стержневым идеально упругим системам разделение потери устойчивости на два рода вполне допустимо.

Потеря устойчивости I рода по сути дела отражает подход Эйлера к решению задач устойчивости. Характерная особенность этого подхода состоит в том, что при потере устойчивости новая форма равновесия существенно отличается от формы, предшествующей потере устойчивости. Следует отметить, что потеря устойчивости I рода относится к идеализированным системам, которые трудно реализовать на практике. Тем не менее ее использование часто подтверждается экспериментом.

В данной книге теория потери устойчивости 1 рода охватывает большинство приведенных ниже примеров расчета элементов строительных конструкций. Среди них устойчивость центрально сжатых стержней рам (рис. У.5, а), круговых колец и арок (рис. У.5, в), пластинок и оболочек, потеря плоской формы изгиба (рис. У.5, в) и др.

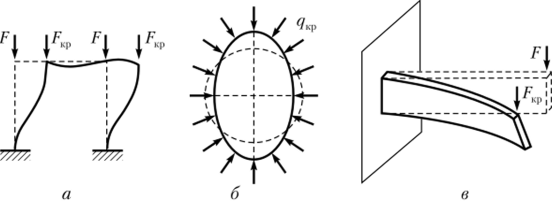
Рис. У.5. Конструкции, подвергшиеся потере устойчивости I рода.

Потеря устойчивости II рода характеризуется сильным развитием предшествовавших деформаций без появления деформаций нового типа (рис. У.6).

Рис. У.6. Потеря устойчивости II рода.

• [1] Прокофьев И. П" Смирнов А. Ф. Теория сооружений, Ч. III. М.: Трансжелдориздат, 1948.