Кинематика эвольвентного зубчатого зацепления

Основным кинематическим условием, которому должны удовлетворять профили зубьев, является постоянство передаточного отношения передачи, т. е.

Для соблюдения этого условия и обеспечения непрерывного зацепления двух зубьев зацепления их сопряженные поверхности должны быть очерчены по кривым, удовлетворяющим основному закону зацеп- 246.

ления. Он формулируется следующим образом: общая нормаль к сопряжённым профилям, проведенная в точке их касания, делит межосевое расстояние на части, обратно пропорциональные угловым скоростям.

Для обеспечения высокого КПД, прочности и долговечности профили колёс должны обеспечивать малые скорости скольжения и достаточные радиусы кривизны в точках их контакта и допускать лёгкое изготовление. Этим условиям наиболее полно удовлетворяет эвольвентное зацепление.

Для передачи силы давления одного зуба на другой в точке их контакта должна быть общая нормаль NN (рис. 37) к сопряжённым профилям зубьев, которая пересечёт линию центров вращения 0)Oi в точке П, называемой полюсом зацепления.

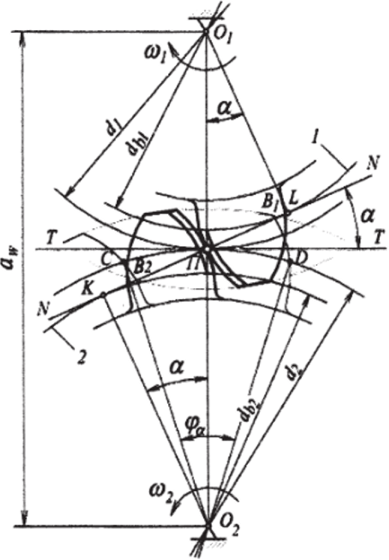
Рис. 37. Элементы эвольвентного зацепления:

1 — ведущее зубчатое колесо; 2 — ведомое зубчатое колесо Окружности с диаметрами d и dfe, проходящие через полюс, называются начальными. Окружная скорость точек, лежащих на этих окружностях, одинакова и равна.

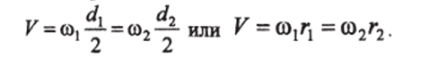
В эвольвенты ом зацеплении любая точка прямой NN перекатывается без скольжения по неподвижной окружности. Линия NN называется производящей прямой, а окужности d_bx и d_b2, по которым эта прямая перекатывается основными окружностями. Основные окружности имеют постоянный диаметр, поэтому нормаль NN и полюс П будут занимать постоянное положение, следовательно, точка контактов зубьев перемещается по общей нормали и называется л и н и е й зацепления.

При изменении межосевого расстояния a_w начальные окружности d и d₂ перестанут касаться друг друга в полюсе Я, то есть появятся новые начальные окружности с новым полюсом. В связи с этим окружности d_x и d₂ не зависят от межосевого расстояния и называются делительными. Если межосевое расстояние равно полусумме диаметров делительных окружностей, то начальные и делительные окружности совпадают. Таким образом, понятие начальная окружность — понятие кинематическое и для отдельно взятого зубчатого колеса не существует. Основные параметры зубчатого колеса определяются по делительной окружности.

Угол, а между линией зацепления NN и общей касательной 7 Т к начальным окружностям называется углом зацепления. Для эвольвентного зацепления, а = 20°. Так как d_bx — d_x COS a; d_b2 = d₂ cosa, то передаточное отношение будет.

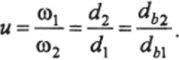
Участок ВВ₂ линии зацепления NN, заключённый между окружностями вершин зубьев называется активной линией зацепления.

Часть профиля зуба, по которой происходит взаимодействие с зубом парного колеса, называется активным профилем зацепления (на рис. 36 активные профили заштрихованы).