Разложение функций в степенные ряды. 
Ряд Тейлора

Будем говорить, что функция f (z) разлагается в области U в степенной ряд, если эту функцию можно представить в виде суммы степенного ряда, сходящегося в каждой точке области U; другими словами, можно подобрать числа zq, cq, ci, C2 .такие что.

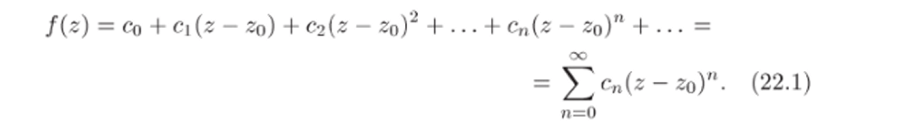
Следующая теорема позволяет находить коэффициенты разложения (22.1) при условии, что такое разложение существует.

Те о р е м, а 22.1 (теорема единственности разложения функции в степенной ряд). Пусть в некотором круге U = {z: z — z$ < < Я} функция f (z) разлагается в степенной ряд. Тогда f (z) является аналитической в U функцией, а коэффициенты co, ci, C2 … разложения определяются однозначно по формулам

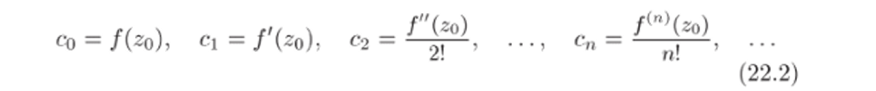
Доказательство. По условию теоремы ряд (22.1) сходится в 1^г и его сумма S (z) = f (z). Поэтому аналитичность функции f (z) сразу следует из свойства 21.С. Чтобы получить первое равенство в (22.2), положим в (22.1) z = zq. Тогда все слагаемые, начиная со второго, обратятся в нуль, и мы придем к равенству /(zq) = со, которое нам и требовалось. Для вывода остальных формул в (22.2) воспользуемся свойством 21.8 и формулами (21.9) (21.11). Подставляя в эти формулы S (z) = f (z) И Z = Zq, ПОЛуЧИМ.

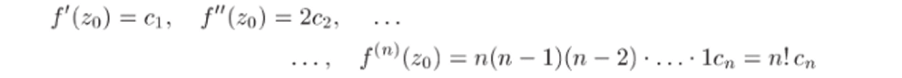
(остальные слагаемые в формулах (21.9)—(21.11) будут содержать множитель (zq — Zq) и поэтому обратятся в нуль). Из полученных равенств сразу следуют формулы (22.2), и теорема 22.1 доказана.

Если положить f⁽⁰⁾(zo) = /(го) ^и 0! = 1, то все равенства (22.2) можно записать единообразно:

Формулы (22.2), (22.3) называются формулами Тейлора. Степенной ряд (22.1), коэффициенты которого определяются по формулам Тейлора (22.3), называется рядом Тейлора функции f (z). Подставляя равенства (22.2), (22.3) в (22.1), получим.

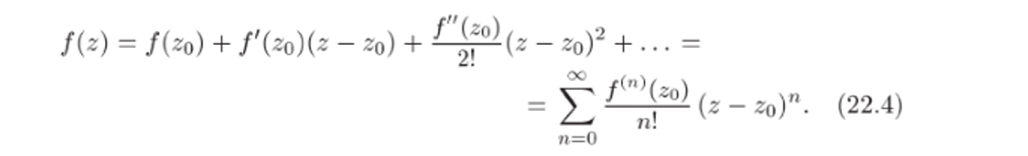
Теорема 22.1 показывает, что если функцию f (z) можно разложить в степенной ряд в некоторой окрестности U точки zo, то это разложение будет рядом Тейлора (22.4) и никаким другим. При этом f (z) должна быть аналитической в U. Следующая фундаментальная теорема утверждает, что для всякой аналитической функции f (z) такое разложение возможно.

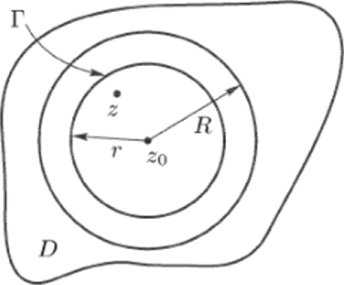
Теорема 22.2 (о существовании разложения аналитической функции в степенной ряд). Пусть функция f (z) аполитична в области D и zq — произвольная точка из D. Тогда в любом, круге, U = {z: z — Zo < 7?}, принадлежащем области D. эту (функцию можно представить в виде суммы, сходящегося степенного ряда Тейлора (22.4).

Доказательство. Возьмем в круге U произвольную точку z и выберем число г так, чтобы z — — zo < г < R (рис. 40). Обозначим через Г окружность |С — zq = г. По интегральной формуле Коши (18.1) имеем.

р_ис ^ Чтобы получить разложение функции.

^ f (z) в степенной ряд, разложим вна чале в ряд функцию -—-. Напомним, что при q < 1.

S ^— z

Это равенство следуеч из формулы для суммы бесконечно убывающей геометрической прогрессии, а также было получено в примере 20.1. Имеем

Положим q = ^z.——. Так как z — zo < |С — Зо|" то q < 1. Поэтому С, — zq.

применима формула (22.6), которая дает.

Для фиксированных точек z и zq и произвольной точки? € Г.

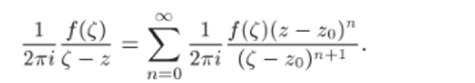
Заметим, что числа о_п не зависят от ?. Так как ——— = q < 1, то числа а_п образуют бесконечно убывающую геометрическую прогрес;

ос сию и, следовательно, ряд ^ач сходится. Поскольку равенства (22.8).

п=о выполнены для всех точек? G Г, то в силу признака равномерной сходимости Вейерштрасса (теорема 20.2) ряд (22.7) сходится на Г абсолютно и равномерно по переменному? (мы уже отмечали, что теоремы 20.2−20.4 п замечание 20.5 справедливы не только для рядов, сходящихся в области, но и для рядов, сходящихся на кривой). Домно;

жим обе части равенства (22.7) на функцию г—г /©, ограниченную.

2пг

на Г; согласно замечанию 20.5, равномерная сходимость ряда (22.7) при этом не нарушится:

Воспользуемся теперь теоремой 20.4, в силу которой получившийся ряд можно почленно интегрировать на Г по переменному ?. Интегрирование и формула (22.5) дают.

(мы воспользовались тем, что множители (z — z$)ⁿ не зависят от (и их можно вынести за знаки интегралов). Таким образом, возможность разложения функции f (z) в степенной ряд установлена. По теореме 22.1 это разложение единственно, т. е. степенной ряд является рядом Тейлора функции f (z). Теорема 22.2 доказана.

Замечания. 1. Тот факт, что полученное разложение (22.9) функции f (z) является рядом Тейлора, можно было обосновать и без ссылки на теорему 22.1. Действительно, коэффициенты с_п этого раз (это равенство справедливо и при п = 0, поскольку обращается в интегральную формулу Коши (22.5)). Отсюда и из (22.10) получаем с_п = /^(п)(г₀)/п! Таким образом, ряд (22.9) является рядом Тейлора функции f (z).

• 2. Из теоремы 22.2 следует, что радиус сходимости ряда Тейлора (22.4) равен расстоянию от центра Zo до ближайшей к нему особой точки функции f (z) (напомним, что особыми называются точки, в которых f (z) не является аналитической). Действительно, пусть z* - ближайшая к Zo особая точка и R = |z* — zq. Тогда функция f (z) будет аналитической в круге U = {z — zq < R] и, согласно теореме 22.2, ее ряд Тейлора сходится в U. Поэтому радиус сходимости ряда (22.4) не может быть меньше R. Но он не может быть и больше R: в противном случае z* была бы внутренней точкой круга сходимости степенного ряда и, следовательно, сумма f (z) этого ряда являлась бы аналитической функцией в 2*, что противоречит условию.
• 3. Согласно теоремам 22.1 и 22.2, функция f (z) является аналитической в области D тогда и только тогда, когда в окрестности каждой точки zq 6 D ее можно представить в виде суммы степенного ряда. Тем самым мы доказали эквивалентность определения аналитичности, данного в и. 3 § 6, и следующего классического определения: однозначная функция f (z) называется аналитической в D, если в окрестности каждой точки zo € D ее можно разложить в ряд по степеням z — Zq.

Формулы (22.3) Тейлора и формулы для производных (e^z)' = е~, (sin z)‘ = cos г, (cos z)' = — sin 2, выведенные в §§ 11,12, позволяют легко получить тейлоровские разложения функций е^г, sin 2 и cos2, аналогичные разложениям соответствующих функций действительного переменного:

(здесь zo = 0). Ряды (22.11)—(22.13) сходятся во всей комплексной ложения определяются равенствами (22.10). По формулам (18.4) (Коши) для производных.

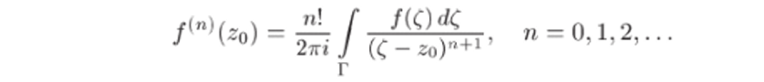
плоскости С. Этот факт можно проверить непосредственно, но признаку Даламбера (см. пример 21.2, в котором рассмотрен ряд (22.11)), а можно вывести из теоремы 22.2. Действительно, поскольку функции е~, sin 2, cosz аналитичны во всей комплексной плоскости (этот факт был установлен в §§ 11, 12), то по теореме 22.2 указанные ряды будут сходиться в любом (сколь угодно большом) круге z < < /?, а значит, и во всей плоскости С; радиус сходимости здесь равен оо.

Замечание. Формулы (22.11)—(22.13) можно принять в качестве определения функций е^г, sin г, cos г. В этом случае формула Эйлера е^гу = cos у + г sin у и равенства sin г = ^ (e^tz — e~^lz), cosг = 1.

= - (e^1z + е^-1'), ранее служившие определениями, теперь будут следствиями формул (22.11) (22.13). Покажем, например, как получается формула Эйлера. Умножим ряд (22.12) на i и сложим с рядом (22.13), располагая члены полученного при этом ряда в порядке возрастания степеней:

Получить его можно либо используя формулу (22.G) для суммы геометрической прогрессии (здесь q = —г), либо непосредственно, но формулам (22.3). Данная функция имеет единственную особую точку z* — —1. Поскольку расстояние от точки zq — 0 до г* равно 1, то радиус сходимости R = 1 (см. выше замечание 2); доказать этот факт можно и по признаку Даламбера. Кругом сходимости будет круг z < 1.

Формулы (22.11)—(22.14) позволяют получать разложения в ряд Тейлора и многих других функций. Полезными при этом часто оказываются следующие приемы: а) метод подстановки; б) почленное интегрирование или дифференцирование рядов.

Пример 22.3. Найти разложение функции f (z) = ¹ ₂ в сте;

пенной ряд с центром zo = 0 и указать радиус сходимости.

Решение. Равенство (22.14) справедливо при любом z, для которого z < 1. Поэтому мы можем подставить в него z² вместо z при условии, что z² < 1:

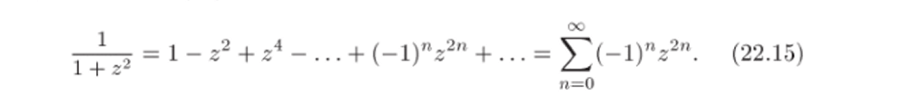
Так как условие z² < 1 равносильно тому, что z < 1, то R = 1.

На примере ряда (22.15) покажем, насколько важно распространение функций с действительной оси в комплексную плоскость для анализа поведения степенных рядов действительного переменного.

Из (22.15) следует, что разложение функции fix) = —- в ряд по.

14-х;

степеням х имеет вид.

Этот ряд сходится в интервале (—1,1) и расходится при х > 1. Причину этого нельзя понять, рассматривая только точки оси ОХ: ведь функция f (x) = — — «одинаково хороша» во всех точках действительной оси, и точки ±1, разделяющие интервалы сходимости и расходимости, ничем не примечательны для этой функции. Но выход в комплексную плоскость сразу разъясняет явление: функция f (z) = --j

1 4″ z

имеет особые точки г* = ±г, расстояние от которых до точки zq = О равно 1. Поэтому и радиус сходимости R = 1.

Пример 22.4. Разложить функцию /(г) = 1п (1 4- z) по степеням z и найти круг сходимости.

Решение. Напомним, что главная ветвь логарифма определяется формулой w = In |ic| 4- i argw, и (In w)' = l/w (cm. § 11). Поэтому функция /(О = ln (l 4- С) является первообразной функции ^.

причем /(0) = 1п1 = 0. Функция ^ ^ ^ имеет единственную особую точку z* = — 1 и, следовательно, аналогична в круге |f| < 1. По формуле (17.4) (Ньютона-Лейбница)

Так как ряд (22.14) сходится в круге z < 1, то его можно проинтегрировать в этом круге:

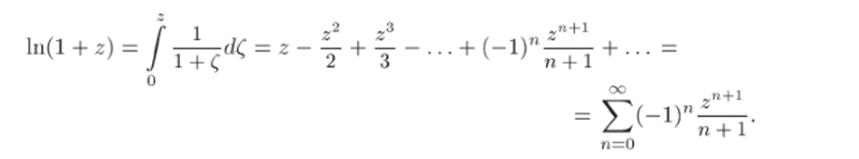
Удобно начинать суммирование с индекса к = 1, сделав замену к =.

= 7i + 1:

Круг сходимости проинтегрированного ряда (22.16) будет тот же, что и у исходного ряда (22.14), т. е. z < 1.

Пример 22.5. Разложить функцию.

в ряд Тейлора в окрестности точки zq = 1 и найти круг сходимости.

Решение. Сделаем замену переменного: z — zo = tv, т. е. w — z -

• — 1, z = w 4- 1. Тогда— =——- =-Чтобы воспользовать-
• 2 — 3 u; + 1 — 3 w — 2

ся формулой (22.14), вынесем в знаменателе за скобки множитель.

(—2): — = ——-77—. Подставляя в (22.14) —w/2 вместо 2, полу;

w — 2 —2(1 — w )/2)

ЧИМ.

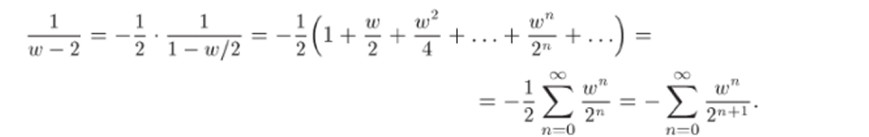
Так как ряд (22.14) сходится при z < 1, то полученный ряд сходится при | - w/2| < 1 или при w < 2. Возвращаясь к переменному 2, подставим w = z — 1:

и искомое разложение получено, причем ряд сходится при z — 1| < 2. Заметим, что круг сходимости можно было определить и из других соображений: функция f (z) =— имеет единственную особую точку.

Z о.

z* = 3. расстояние от которой до центра zo = 1 ряда равно 2. Поэтому радиус сходимости R = 2 и круг сходимости есть z — 1| <2.

Точка г₀ называется нулем функции f (z), если /(г₀) = 0. Предположим, что функция f (z) аналогична в некоторой окрестности U точки го, /(го) = 0 и /(г) не обращается в нуль тождественно в этой окрестности. В V функция /(г) разлагается в ряд Тейлора. Так как /(г₀) = 0, то коэффициент Со тейлоровского разложения (22.1) функции /(г) равен нулю (см. (22.2)). Поскольку /(г) не равна нулю тождественно в U, то среди остальных коэффициентов найдется хотя бы один ненулевой. Номер п первого отличного от нуля коэффициента е_п называется кратностью или порядкам, нуля гоПри этом разложение функции /(г) в окрестности точки го имеет вид.

где с" ф 0 и п ^ 1. Из (22.2) следует, что порядок нуля го равен порядку младшей отличной от нуля производной /^(гг)(го). Если п = 1, то нуль го называется простым.

Разложение (23.1) можно переписать в виде.

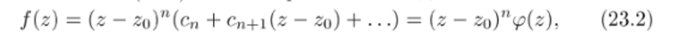
где ip (z) = с_п + Cn+i (z — г₀) + …, причем <*?(го) = с" Ф 0.

П р и м е р 23.1. Найти нули функции /(г) = (г² — 4)³е^г и указать их порядок.

Решение. Уравнение /(г) = 0 равносильно тому, что г² — 4 = 0, или г = ±2. Представим /(г) в виде /(г) = (г — 2)³(г + 2)³е~. Пусть го = 2. Положим <^(г) = (г + 2)³е^г. Тогда /(г) = (г — 2)³<^(г), причем <�р (2) = 4³е² ф 0. Поэтому го = 2 нуль порядка 3. Если же го = —2, то возьмем ip (z) = (г — 2)³е^г. Из равенства /(г) = (г 4- 2)³у?(г), в котором у>(—2) ф 0, следует, что го = —2 — также нуль порядка 3.

Теорема 23.2. Пусть (функция, /(г) аполитична в некоторой окрестности U точки го, /(го) = 0 и /(г) не равна нулю тождественно в U. Тогда существует окрестность точки го, в которой f (z) не имеет других нулей, кроме го;

Доказательство. Пусть го нуль порядка п. Тогда справедливо равенство (23.2). Функция у?(г) является аналитической, а значит, и непрерывной в U, причем p (zo) ф 0. Поэтому найдется такая ок1хч'тность (возможно, меньшая) точки го, в которой у?(г) ф 0. Так как множитель (г — го)^п обращается в нуль только в точке го, то в указанной окрестности функция /(г) = (г — zo)ⁿip (z) также обращается в нуль лишь при г = го, что и т!>ебовалось доказать.

Будем говорить, что точка го является изолированным нулем функции/(г), если найдется такая окрестность точки го, в которой f (z) не имеет нулей, отличных от zq. Теорема 23.2 утверждает, что аналитическая функция, не равная тождественно нулю, может иметь только изолированные нули. Выведем отсюда следующую важную теорему.

Теорема 23.3 (теорема единственности). Если две аналитические в области D функции f (z) и /0(2) совпадают на некоторой бесконечной последовательности попарно различных точек Zi, z-2,…, сходящихся к точке а € D, то fi (z) = /2(2) всюду в области D.

Доказательство. Рассмотрим функцию /(z) = J (z) — — /2(2). Она аналогична, а значит, и непрерывна в D, и f{z_n) = О,.

п = 1.2,… Поскольку lim z_n = а и f (z) непрерывна в а, то /(а) =.

п-эоо.

= lim f (z_n) = 0. Поэтому а — тоже нуль функции /(2), причем нуль п—юо

не изолированный, гак как в любой окрестности точки а найдется бесконечно много других нулей z_n.

Возьмем произвольную окрестность U точки о, лежащую в D. Тогда функция f (z) аналитична в U. Предположим, что в U функция /(2) не обращается в нуль тождественно. Тогда по теореме 23.2 точка а должна быть изолированным нулем, и мы придем к противоречию. Следовательно, /(г) тождественно равна нулю в любой окрестности точки а, лежащей в D. Докажем, что f (z) равна нулю во всех точках области D. Пусть 6 — произвольная точка области D. Соединим точки а и b непрерывной кривой Г, лежащей внутри D. Пусть р — кратчайшее расстояние от точек кривой Г до границы области D. Возьмем некоторое положительное число 6 < р (например, 6 =.

= р/2). На кривой Г выберем ТОЧКИ Шо> Wl, • • • i^wn ТИК, чтобы wo = a, w_n = b и расстояние между каждыми двумя соседними точками было меньше 6. Для каждой точки Wk построим круг Uk с центром Wk и радиусом б ^ис* ⁴¹

(рис. 41). Поскольку б < р, то все эти круги будут целиком лежать в D. Так как Uq является окрестностью точки а = wo, то f (z) = 0 (т.е. тождественно равна нулю) в Uq. По построению расстояние между точками wq и u’i меньше б. Поэтому w лежит внутри круга Uq значит, и некоторая (малая) окрестность точки w лежит в Щ. В этой окрестности f (z) = 0, и, следовательно, wi не является изолированным нулем функции /(2). Так как /(г) аналитична в окрестности U1 точки «ц, то /(2) е0 в 1/| (в противном случае, согласно теореме 23.2, нуль w 1 был бы изолированным). Переходя теперь от круга U к U-2 и проводя аналогичное рассуждение, мы получим, что /(г) = 0 и U-2- Двигаясь по цепочке кругов, мы доберемся до U,_} и покажем, что f (z) = 0 в U_n. В частности, /(6) = 0. Таким образом. f (z) = fi (z) — /2(2) = 0 во всех точках из D. Следовательно, fi (z) = /2(2) всюду в области D, что и требовалось доказать.

Теорема 23.3 показывает существенное отличие дифференцируемости функций комплексного переменного от дифференцируемости функций действительного переменного. В самом деле, две даже бесконечно дифференцируемые функции действительного переменного.

Рис. 42.

могут совпадать на части области определения, нс совпадая тождественно. Например, функции.

(рис. 42) бесконечно дифференцируемы, совпадают при х € (—1,0], но /Дг) Й /2(2) на (—1,1). В 1чз же время, согласно доказанной теореме 23.3, если две аналитические в D (т.е. дифференцируемые всюду в D) функции совпадают на множестве, содержащем последовательность точек, сходящихся к точке а € D (например, совпадают на маленьком кружке или на дуге, принадлежащей области D), то эти функции совпадают во всей области D.

Выведем из теоремы 23.3 еще одно важное свойство аналитических функций.

Теорема 23.4 (принцип максимума модуля). Пусть функция f (z) аполитична в ограниченной области D, непрерывна в замкнутой области D и не является постоянной. Тогда максимум модуля. |/(г)| (функции /(г) в замкнутой области D достигается только на границе области D.

Доказательство. Функция |/(г)| непрерывна в замкнутой ограниченной области D и, следовательно, принимает свое наибольшее значение А/ в некоторой точке zq 6 D. Надо доказать, что zo не может быть внутренней точкой области D. Пусть это неверно, т. е. zo € D и f (zo) = Л/. Докажем, что тогда и в любой окрестности U точки 2о, целиком лежащей в D. выполнено равенство |/(, г)| = А/. Пусть z — zo = R — окружность настолько малого радиуса R, что замкнутый круг |z — zo ^ R целиком лежит в D. По теореме о среднем (теорема 18.3)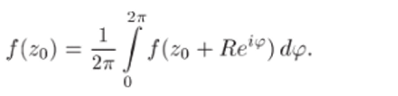

Отсюда следует —.

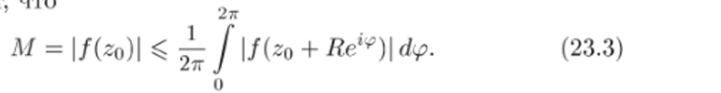
Если найдется такое ||,?0)| < Л/, то в силу непрерывности функции f (z) найдется также интервал (ро — 6, + <$), на кото ром |/(zo + Яе¹^)! < А/. Поскольку в остальных точках отрезка [0,27т] выполнено неравенство f (zo + Re¹*)| ^ А/ (так как М — наибольшее значение f (z) в .D), то тогда правая часть (23.3) будет строго меньше Л/, что противоречит равенству в (23.3) (получится М < М). Значит, для всех ip 6 [0,27г] будет |/(го + Re¹*)| = А/. Так как R произвольное достаточно малое число, то f (z) = Л/ и во всей окрестности U точки Zo-

Покажем теперь, что не только |/(г)|, но и сама функция f (z) является постоянной в U. Тем самым теорема будет доказана. Действительно, если f (z) = с в t/, то по теореме 23.3 f (z) = с во всей области D, что противоречит условию о том, что f (z) не является постоянной. Таким образом, предположив, что zq — внутренняя точка области D. мы придем к противоречию.

Если М = 0, то равенство f (z) = 0 равносильно тому, что f (z) = О в U, что нам и требовалось. Рассмотрим теперь случай М > 0. Так как /(го) Ф 0, то в некоторой окрестности точки zq можно выделить регулярную ветвь y (z) многозначной функции Ln f (z) (о регулярных ветвях логарифма см. § 11). Для действительной части функции y (z) имеем Re<7(z) = ln|/(z)| = InM. Поэтому функция u (z) = Re</(z) является постоянной в некоторой окрестности точки Zq. Используя условия Коши Римана

получим, что мнимая часть v (z) функции y (z) также постоянна. Поэтому y (z) = ci. Так как f (z) — e⁹'^z то f (z) = e^Cl = с, т. е. f (z) тождественно равна постоянной в некоторой окрестности точки zq. Теорема 23.4 доказана.

Замечания. 1. Теорему 23.4 легко вывести из теоремы 23.3 и следующего принципа сохранения области (свойство 13.2): если функция f (z) аполитична в области D и отлична от постоянной, то множество D', на которое она отображает D, также является областью (т.е. открытым связным множеством). Попробуйте доказать теорему 23.4 таким способом самостоятельно. Выше мы привели более сложное рассуждение потому, что указанный принцип сохранения области был сформулирован в § 13 без доказательства.

2. Теорему 23.4 можно сформулировать в следующем эквивалентном виде: если функция f (z) аполитична в области D и ее модуль f (z) достигает максимума (локального) в некоторой точке zq € D, то f (z) постоянна.