Интерферограмма и восстановление оптическою спектра из интерферограммы

Рассмотрим подробно процедуру формирования фурьеспектрометром спектра излучения источника^[1] в оптически идеальном случае при неограниченном перемещении подвижного зеркала. Допустим сначала, что источник ИК-излучсния является точечным и монохроматическим с волновым числом у. Падающее на идеальный (не поглощающий и в равных долях отражающий и преломляющий свет) светоделитель монохроматическое излучение делится на две равные по амплитуде световые волны 3 и 3 В зависимости от оптической разности хода между ними попадающее на фотоприемник излучение либо усиливается, либо ослабляется. Пусть одно из зеркал (М₂ на рис. 1.1) перемещается с нормальной к его поверхности постоянной скоростью и вдоль оптической оси прибора. Тогда через изображение точечного источника в выходной фокальной плоскости прибора (точка Г) проходит переменный поток излучения Ф_ф1/(А), описываемый формулой двухлучевой интерференции.

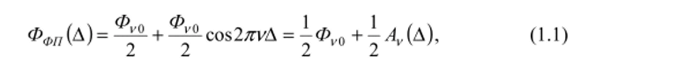
где Ф_уо — поток монохроматического излучения на входе интерферометра, 2яуД — разность фаз колебаний волн 3 и 3' в точке /, А = Д (/) — оптическая разность хода интерферирующих волн, линейно зависящая от времени.

Второе слагаемое в формуле (1.1) изменяется с изменением оптической разности хода, а значит, и со временем:

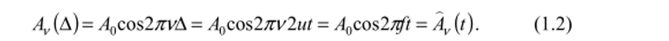
Таким образом, поток монохроматического излучения источника на выходе спектрометра оказывается промоделированным во времени. В формуле (1.2) А₀ — амплитуда модуляции, которая является константой, а / = vA/t — частота модуляции сигнала на выходе интерферометра, которая зависит от скорости передвижения зеркала и и волнового числа v. Каждому монохроматическому излучению с волновым числом v соответствует своя интерференционная косинусоида (рис. 1.2 а).

Если на идеальный интерферометр падает излучение, лежащее в диапазоне волновых чисел от и, до v₂, то регистрируемый фотоприемником суммарный поток излучения в этом диапазоне описывается выражением.

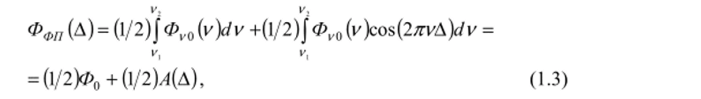
где Фу${у) — спектральная плотность потока излучения, то есть оптический спектр.

Сигнал, регистрируемый фотоприемником фурье-спектрометра, представляет собой интерферограмму. Часто [1,2,4] интерферограммой называют только второе переменное слагаемое в выражении (1.3), которого одного достаточно для воссоздания оптического спектра. В дальнейшем будем опускать множитель ½ и назовем интерферограммой переменную функцию Л (д), которая имеет вид.

Как было показано (1.1), интерферограмма монохроматического излучения представляет собой косинусоиду с постоянной амплитудой (рис. 1.2 а). В случае спектров, непрерывных на некотором интервале (см. рис. 1.2 в-г), интерферограммы имеют следующие общие черты. Вопервых, все интерферограммы Л"(Д) отдельных монохроматических составляющих находятся в фазе при нулевой разности хода. Иначе говоря, излучение на всех волновых числах усиливается при нулевой разности хода, а величина А (а) в этой точке принимает наибольшее значение что позволяет находить на интерферограмме точку, соответствующую нулевой разности хода. Во-вторых, контрастность'* интерферограммы снижается тем быстрее, чем больше протяженность спектра, что видно при сравнении модельных спектров Ф_у(у) и интерферограмм Л (д), приведенных на рис. 1.2 (в) и (г) (тонкие и толстые линии).

В общем случае пределы интегрирования в (1.4) можно изменить:

тогда интерферограмма будет представлять собой косинус-преобразование Фурье, или фурье-образ, спектра излучения источника Ф_{у ()}(у). Таким образом, фотоприемником непосредственно регистрируется нс реальный оптический спекгр, а его фурье-образ.

Поскольку преобразование Фурье является обратимой операцией, фурье-анализ позволяет преобразовать интерферофамму Л (Д) в оптический спектр.

Рассмотрим подробнее процедуру преобразования. В общем случае функция F (jr), удовлетворяющая условию Дирихле на любом конечном отрезке и такая, что интеграл от ее модуля в бесконечных пределах сходится, может быть записана в виде^[2]

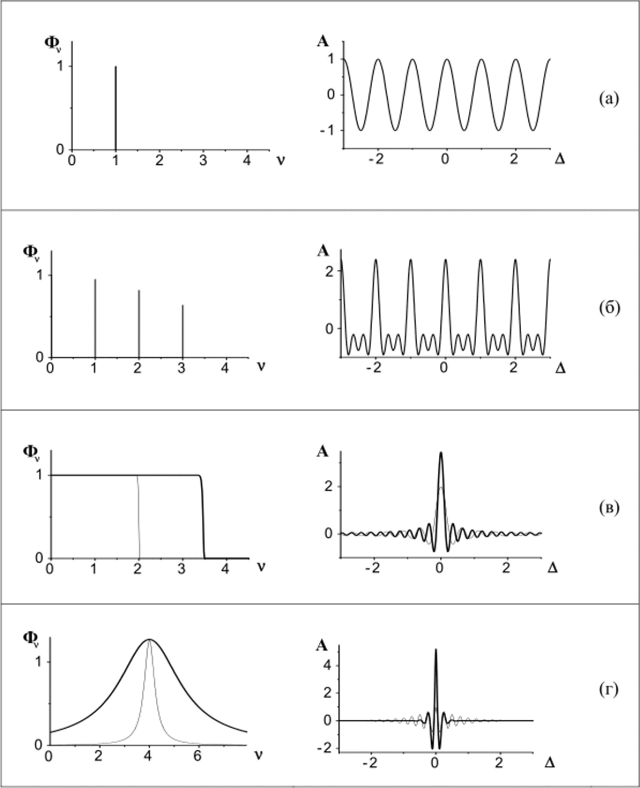
Рис. 1.2. Модельные спектры Ф_у{у) и соответствующие им интерфер01раммы Л (Д) (в условных единицах). Спектр (г) описывается функцией Лоренца.

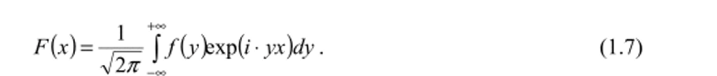
Выражение в правой части (1.7) называется интегралом Фурье функции F (x). Подынтегральная функция /(у) называется фурье-спектром или фурьс-образом функции F (x), а переменные х и у — сопряженными параметрами. Функция f (y), в свою очередь, может быть выражена интегралом.

Если функция F (x) — действительная и четная, то есть F (x)=F (- л:), то, используя формулу Эйлера exp (/xv') = cos (A-_y) + /sin (jr>').

и понятие комплексного сопряжения, можно доказать, что.

Возьмем в качестве переменных оптическую разность хода Д и волновое число у, перейдем к исходным обозначениям функций и установим соответствие между математически восстанавливаемым из интерферограммы спектром Фу₀ и истинным спектром Ф_у0. Функция Л (Д) не зависит от знака оптической разности хода и является действительной четной функцией, симметричной относительно Д = 0. В силу вышесказанного восстанавливаемый спектр можно получить с помощью косинус-преобразования Фурье:

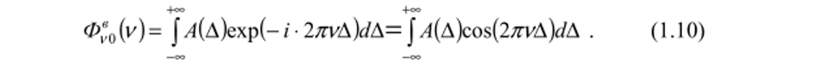
Математически восстановленная функция Ф*₀ является, в свою очередь, действительной и четной: Ф*₀(у) = Ф*₀(—у). Обратное фурье-преобразование такой функции Ф"₀ должно приводить к исходной интерферограмме:

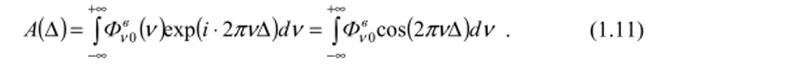
Сравнивая выражения (1.6) и (1.11), приходим к следующей связи между Ф«о и Ф,₀:

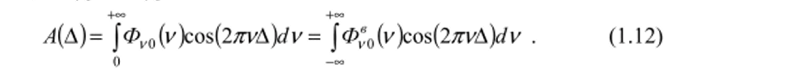
³⁾ Подробнее смотри, например, [5,6].

Истинный спектр Ф_у0 определен только для реально существующих положительных волновых чисел, а для отрицательных он равен нулю, в то время как фурье-преобразование интерферограммы (1.10) формирует спектр Фу₀ также и в области отрицательных волновых чисел. В качестве примера па рис. 1.3 приведен спектр, восстановленный из интерферограммы монохроматического излучения с волновым числом v_t.

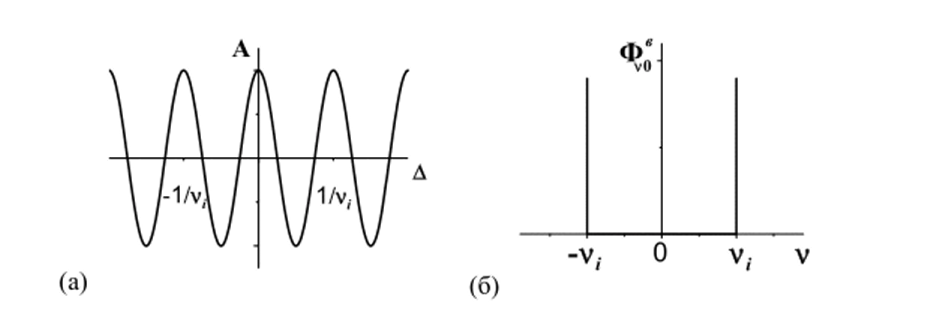
Рис. 1.3. Интерферограмма Л (Д) монохроматического излучения с волновым числом v, (а) и спектр Ф*₀, восстановленный из нее оптически идеальным фурье-спектрометром с неограниченной оптической разностью хода, А (б).

Функция, принимающая отличные от нуля значения только для положительных волновых чисел, может быть представлена как сумма четной и нечетной составляющих (рис. 1.4).

Восстановленный фурье-преобразованием спектр Ф*₀ есть не что иное как четная часть истинного спектра. Значения восстановленного спектра в два раза меньше соответствующих значений истинного спектра при имеющих физический смысл положительных волновых числах, а в области отрицательных волновых чисел восстановленный спектр имеет симметричные относительно нулевого волнового числа значения.

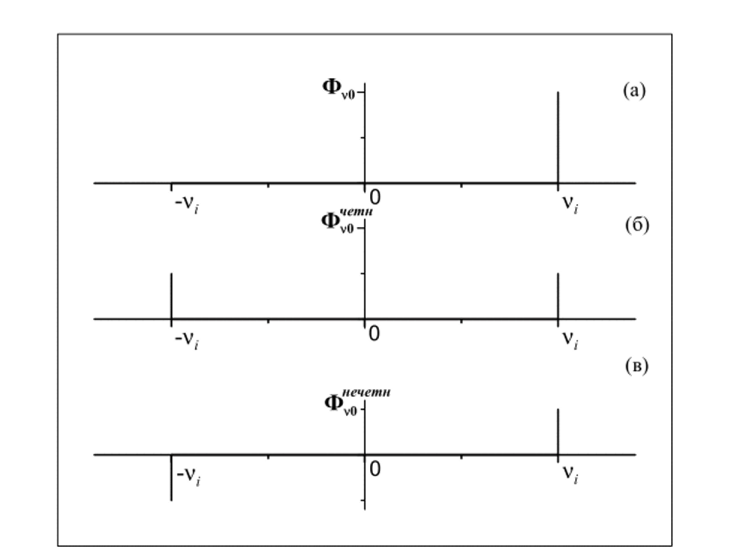
Рис. 1.4. Разложение спектра Ф,₀ (а) на четную (б) и нечетную (в) составляющие.

Разность хода в конкретном интерферометре может принимать как отрицательные, так и положительные значения, но вследствие четности интерферограммы Л (Д) достаточно знать ее вид при положительных значениях Д. Интерферограмма, измеренная при Д>0, называется односторонней. При регистрации односторонних интерферограмм по сравнению с двусторонними вдвое сокращается величина, а значит, и время перемещения подвижного зеркала, а также объем обрабатываемой информации. Нулевую разность хода в этом случае обычно определяют путем регистрации односторонней интерферограммы с небольшим отрицательным смещением. Все последующие математические преобразования относятся к односторонней интерферограмме^[3]*.

Далее будем обозначать восстановленный из интерферограммы спектр как Ф_у0, опуская коэффициент перед интегралом.

и рассматривать получаемый спектр как четный.

Ф_у0 есть спектральная плотность потока монохроматического излучения при определенном значении волнового числа у. Для того чтобы восстановить весь оптический спектр, необходимо провести аналогичные преобразования для каждого волнового числа исследуемого спектрального интервала.

• [1] 2> Получение с помощью фурье-спектрометров спектров пропускания и поглощения рассматривается в разделе 6.
• [2] Контрастность интерферофаммы есть отношение (Атах — Атш)/(Атих + Ат1п).
• [3] При восстановлении спектра из двусторонней интерферограммы, зарегистрированной при одинаковых максимальных положительных и отрицательныхзначениях оптической разности хода, нс требуется точного определения нулевой разности хода. Искомый спектр восстанавливается в этом случае не косинус-, а полным фурьс-прсобразованисм.