Последовательные алгоритмы решения задачи поиска с отношением поиска вида линейного предпорядка

Пусть, а? X, Ка —.

I

функция, действующая из X в {0,1}, такая что N^_a = {х € X: х У а}.

Будем рассматривать базовое множество То = (?, 0). Так как оно содержит характеристические функции всех записей, то То полно для типа Sun•.

Отметим, что К_а(х) есть характеристическая функция записи а. Пусть АС = {АГ_а(х): а 6 X}.

Прежде чем привести формулировку и доказательство основного утверждения данного раздела, докажем несколько вспомогательных утверждений.

Мы не можем воспользоваться теоремой 21 о существовании главных цепей, поскольку в ней предполагается конечность множества запросов Х_} а в этом разделе мы этого не предполагаем. Поэтому мы вынуждены отдельно доказывать существование главных цепей в случае, когда отношение поиска является отношением линейного предпорядка.

Лемма 32. Пусть U — произвольный ЛИГ над базовым множеством То = (АС, 0). Пусть В — произвольное характерное подмножество вершин графа U. Тогда в графе U существует главная цепь множества В.

Доказательство. Отметим, что конъюнкция любых функций из К. есть функция из АС, также как дизъюнкция любых функций из )С есть функция из АС, т. е. операции конъюнкция и дизъюнкция не выводят из множества JC.

Для того, чтобы без переобозначений воспользоваться некоторыми свойствами из раздела 3.1 введем множество.

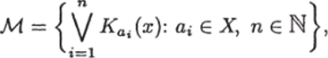
где N — множество натуральных чисел, хотя в данном случае в силу сделанного выше замечания М = АС.

Так как при доказательстве свойств 1−4 используется только свойство транзитивности отношения и не используется конечность множества запросов, то эти свойства справедливы и в данном случае.

Справедливость свойства 5 следует из того, что конъюнкция любых функций из К, есть функция из К.

Таким образом, и в данном случае проходит доказательство теоремы 21, приведенное в разделе 3.1.

Тем самым, лемма доказана.

Следствие 15. Пусть U — ПИГ над базовым множеством То — = (АС, 0). Тогда для любой достижимой вершины графа U существует главная цепь.

Доказательство. Так как конъюнкция и дизъюнкция любых функций из АС есть функция из АС, то функция фильтра любой достижимой вершины есть функция из АС, и, следовательно, любая достижимая вершина образует характерное множество. Откуда в силу леммы 32 получаем требуемое.

I

Следствие 16. Пусть I = (X, V, У) — ЗИП типа Бц_п. Пусть U — ПИГ над базовым множеством То — (АС, 0), разрешающий ЗИП I. Тогда для любой записи у? V в графе U существует главная цепь записи у.

Доказательство. Полностью аналогично доказательству следствия 10.

I

Теорема 35. Для любой ЗИП I = (X, V, У) типа 5ц_п существует оптимальный ПИГ над базовым множеством То = (АС, 0) и

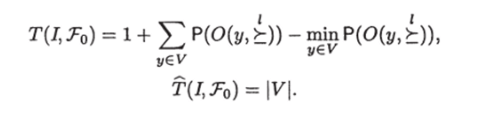
I.

Доказательство. Возьмем произвольную ЗИП I = (X, V, У) типа Sli п- Пусть V = {т/1,г/2) • • •, у*}, причем записи упорядочены так, что.

i l I

yihy2h — —hyk-

Рассмотрим сначала случай сложности ЗИП I.

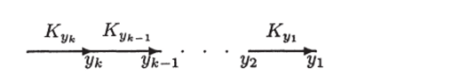
Рис. 3.16. Граф Uo.

Верхняя оценка. Рассмотрим ПИГ Uo, изображенный на рис. 3.16.

Обозначим лист, которому приписана запись у* (г = 1, Дс), через ot{. Так как для любого i 6 {1, к}

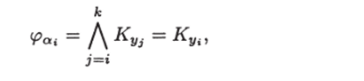
то согласно теореме 1 граф Uo разрешает ЗИП I. Нетрудно подсчитать, что.

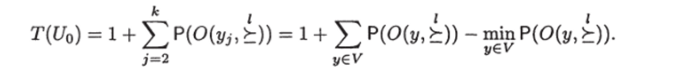
Что и доказывает верхнюю оценку.

Ниэюняя оценка. Возьмем произвольный граф U, разрешающий ЗИП I. Доказательство нижней оценки будем проводить следующим образом. Мы применим к графу U ряд преобразований, которые не меняют функционирования графа и не увеличивают его сложность, и с помощью этих преобразований перейдем от графа U к графу Uo и тем самым докажем, что T (U) ^ T (Uo). Эти преобразования по целям, которые они преследуют, можно разбить на несколько этапов.

I этап. Согласно следствию 16 каждая запись из V имеет главную цепь. Пусть U — ПИГ, состоящий только из главных цепей записей из V, причем в качестве полюсов в U мы оставим только корень и концы главных цепей записей, т. е. каждой записи будет соответствовать ровно один лист. Понятно, что T (U) ^ T (U) и функционирование графа U такое же, что и у графа U, т. е. U разрешает ЗИП /.

II этап. На этом этапе мы от графа U перейдем к графу С/г, разрешающему ЗИП /, такому, что Т (//г) ^ T (?/i) ^и полустепень захода любой вершины графа С/г не больше 1, т. е. С/г имеет вид дерева.

Предположим, что в графе U существуют вершины, полустепень захода которых больше 1. Возьмем произвольную такую вершину и обозначим ее через 0. Согласно следствию 15 существует главная цепь (обозначим ее Ср) вершины 0. Пусть через вершину 0 проходит несколько главных цепей записей, которые обозначим Ci,… , С_т. По построению U имеем т > 0.

Пусть Ci = С}С? (г = 1 ,…, т), где С} — часть цепи С, от корня до вершины 0, а С? — часть цепи С{ после вершины 0 до соответствующей записи.

Поскольку функция фильтра у>р вершины 0 равна проводимости цепи Ср, то, следовательно, <�рр не зависит от проводимости цепей С/, г = 1,…, т. Отсюда мы можем объявить вместо цепей С{ в качестве главных цепей цепи С[ = CpCf (t = 1,…, m) после чего, удалив ребра, не принадлежащие новым главным цепям (в частности, удаляются все ребра, входящие в вершину 0, за исключением ребра, принадлежащего цепи Ср), получим ПИГ U[, который разрешает исходную ЗИП /, имеет сложность, нс превышающую сложность графа U, и имеет меньшее число вершин с полустепенью захода больше 1.

Проделав эту операцию для оставшихся в графе U[ вершин с полустепенью захода больше 1, мы через несколько шагов получим граф и[^г) (г — число не большее, чем число вершин с полустепенью захода больше 1 в сети Uj), который разрешает ЗИП I, имеет сложность, не превышающую сложность графа l/j, и не имеет вершин с полустепенью захода больше 1. Следовательно, и[^г^ имеет вид дерева, и, переобозначив его, мы получим требуемый граф С/г*.

III этап. На этом этапе мы от графа (7г перейдем к графу С/₃, разрешающему ЗИП I, такому, что T (Uz) ^ T (U2) и полустепень исхода любой вершины графа U$ не больше 1.

Если 0 некоторая вершина информационного дерева //г, то высотой вершины 0 назовем количество ребер в цепи, соединяющей корень графа с вершиной 0. Высотой ребра ИД будем считать высоту начала ребра.

Если из некоторой вершины 0 высоты h ИД U2 исходит тп ребер, где га > 1, то будем говорить, что из вершины 0 исходит га — 1 лишнее ребро высоты h, т. е. все ребра, исходящие из 0, кроме одного будем считать лишними высоты h. Таким образом, если в графе нет вершин с полустепенью исхода больше 1, то, значит, в графе нет лишних ребер.

Пусть г — число ребер в графе t/гПонятно, что в графе U2 не может быть ребер высоты, большей, чем г — 1.

Пусть h — параметр, который мы перебираем, начиная с 0 до г — 1, и для каждого h выполняем следующие действия.

Если в графу U2 нет лишних ребер высоты h, то переходим к следующему h. Предположим, что в графе U2 есть t лишних ребер высоты h (t > 0). Возьмем произвольное лишнее ребро (0,у) высоты h. Так как оно лишнее, то из вершины 0 исходит по крайней мере еще одно.

I

ребро. Обозначим его (0,6). В силу свойства связности отношения У всегда либо N_v С N_vs, либо N_tp6 С N^. Без ограничения общности будем считать, что N_Vy С N_4>6. Сложность, вносимая в граф U2 ребрами (0,^) и (0,6), равна 2-Р (/У^). Перенесем начало ребра (0,7) в вершину 6 (т. е. заменим ребро (0,7) на ребро (5,7). Функционирование графа от этого не изменится, так как функции фильтров каждой из вершин 7 и 6 не изменятся, а сложность графа нс увеличится, так как сложность, вносимая в граф ребрами (6, у) и (0,6), равна.

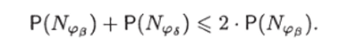
В результате этой операции мы избавимся от одного лишнего ребра высоты h. А проделав эту операцию для оставшихся t — 1 лишнего ребра высоты h, мы избавимся от всех лишних ребер высоты h. Полученный в результате граф опять обозначим через U2 и перейдем к следующему h.

После того как мы переберем все h, мы получим граф (переобозначим его через Uz), в котором не будет лишних ребер, т. е. в нем не будет вершин с полустепенью исхода больше 1, причем он по прежнему разрешает ЗИП I, и сложность его после преобразований не увеличилась.

IV этап. На этом этапе мы от графа Uz перейдем к графу Ua, разрешающему ЗИП /, такому, что T (Ua) ^ Т (С/з) и в графе С/4 нет неполюсных вершин.

Так как в графе Uz полустепени захода и исхода каждой вершины не превышают 1, то, значит, граф Uz имеет вид цепи.

Покажем, что если расположить записи в порядке следования их вдоль цепи, то полученный порядок будет обратным к порядку,.

I

задаваемому отношением У. В самом деле, если предположить, что существуют два листа а и с*2, которым приписаны соответственно записи t/x и уг, таких, что ах встречается вдоль цепи и$ раньше, iiii чем а₂, но 0(ух,>:) С 0(у₂, У) (т.с. ух У у₂ и у₂? ух), то тогда.

/ /.

Лу*₂ С АГу,_а1 = 0(ух, >:), и, следовательно, %_Л2 ^ 0(y₂, h), что противоречит тому, что граф U3 разрешает ЗИП /. Значит, записи вдоль цепи Uz следуют в порядке обратном порядку, задаваемому I

отношением У.

Предположим, что в графе U$ есть неполюсные вершины. Возьмем произвольную неполюсную вершину, которую обозначим через 0. Так как 0 — не корень, то существует полюс, из которого в 0 ведет цепь, не содержащая других полюсов. Обозначим этот полюс через 7. Так как 0 принадлежит некоторой главной цепи записи, то существует лист, в который из 0 ведет цепь, не содержащая других листьев. Обозначим этот лист через S. Так как вершины 7, 0 и 8 следуют вдоль единственной цепи ?/3, то D D N_(ps. Заменим цепь, соединяющую полюсы 7 и S и содержащую вершину 0, одним ребром (7,5), которому припишем предикат В результате получим граф с тем же функционированием, так как функции фильтров листьев не изменятся, с не большей сложностью и с меньшим числом неполюсных вершин. Применив эту операцию для каждой из оставшихся неполюсных вершин, мы в конце концов получим граф {/4, в котором не будет неполюсных вершин, причем он по-прежнему будет разрешать ЗИП /, и сложность его после преобразований не увеличится.

Осталось заметить, что так как граф U не содержит неполюсных вершин, имеет вид цепи, и записи вдоль этой цепи следуют в порядке

I

обратном порядку, задаваемому отношением У, то граф U4 с точностью до равных записей совпадает с графом {/о, изображенным на рис. 3.16.

Тем самым мы показали, что для любого графа U, разрешающего ЗИП /, справедливо T (U) ^ T (Uo).

Откуда с учетом верхней оценки получаем, что.

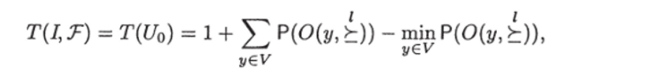
что в свою очередь означает, граф Uq — оптимальный для ЗИП I. Оценим теперь В-сложность ЗИП I.

Согласно мощностной нижней оценке.

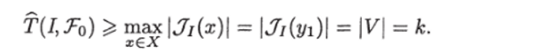
С другой стороны,.

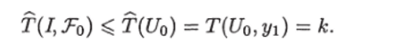
Следовательно, Т (/, То) = к и Uo — В-оптимальный ИГ для ЗИП I Тем самым, теорема полностью доказана.

Следствие 17.

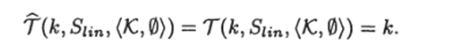
Конечное множество X' С X назовем минимальным подмножеством X, если для любых х' € X' и х" G X X' выполняется х" х¹.

Неотрицательное число п назовем степенью возрастающей пумеруемости множества Х_} если существует минимальное подмножество X мощности п и не существует минимального подмножества X мощности п 4−1.

Если для любого натурального п существует минимальное подмножество X мощности п, то скажем, что степень возрастающей нумеруемости X равна оо.

Если не существует минимального подмножества X мощности 1, то скажем, что степень возрастающей нумеруемости X равна 0.

Следствие 18. Пусть п — степень возрастающей нумеруемости множества X (в том числе может быть п = оо). Тогда, если л ^ 1, то T (fc, Sii_n, (/С, 0)) = к для любого натурального к; если же п > 1, то для любого натурального к ^ п + 1.

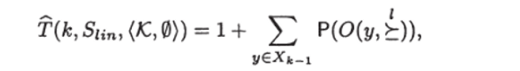
а для любого к > п + 1.

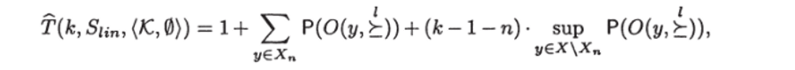
где Х{ — минимальное подмножество X мощности i.