Ударно-отражательные устройства. 
Системный анализ процессов химической технологии: измельчение и смешение

Ударно-отражательные измельчающие устройства, как и ударноцентробежные, относятся к устройствам с высокой скоростью удара. 13 последние годы эти устройства стали с успехом внедряться в различных отраслях промышленности как в нашей стране, так и за рубежом. В отличие от других типов измельчающих устройств они при простоте конструкции являются компактными, имеют меньшие энергозатраты и позволяют получать продукт высокой тонины.

Наиболее совершенными устройствами этого типа являются одноступенчатые и многоступенчатые мельницы ударно-отражательного действия (46—481.

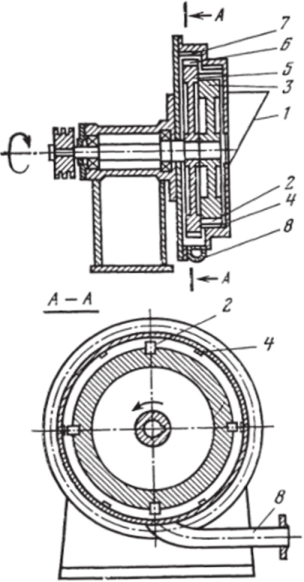
Рассмотрим принципиальную схему двухступенчатой мельницы ударно-отражательного действия (рис. 2.14). Мельница работает следующим образом. Исходный материал питателем через загрузочное устройство 1 подается на первую ступень в зону измельчения. Попадая под быстровращающиеся била 2, закрепленные на роторе 3 первой ступени, исходный материал первично измельчается (нагружается) и отбрасывается на отбойные плиты 4_У где он вторично нагружается. Затем осколки и иеРис. 2.14. Схема двухступенчатой разрушившиеся частицы, отражаясь ударно-отражательного _{QT плит опять попадают под била} действии ••.

и т. д. Из зоны измельчения первой ступени материал попадает на вторую ступень, где он аналогично подвергается измельчению билами 6 на роторе 5 и отбойными плитами 7 второй ступени. Из зоны измельчения второй ступени измельченный материал потоком воздуха тангенциально выводится через выгрузочный патрубок 8 в циклон-приемник.

В работах (46,47, 49—511 разработана математическая модель процесса измельчения в мельнице ударно-отражательного типа для периодического режима работы. Модель имеет следующий вид:

— матрица-столбец размером N X 1 гранулометрического состава измельчаемого. материала, полученного после к-го нагружения или в к-й момент времени (примем, что одно нагружение происходит за один момент времени);

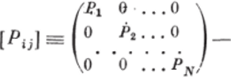
— диагональная матрица вероятностей разрушения размером N X X N_y F_n.y F_ik,.. ., F_Nk — число измельченных частиц соответственно 1,2,…, N-й фракции в к-й момент времени; Рi, Р₂,.. •.. ., Р, — вероятности разрушения частиц coojeeTCTBeHHO 1,2,….. ., Л'-й фракций; N — число фракций частиц или число размерных интервалов; 1 — соответствуют частицам самого маленького размера, а N — самого большого, т. е. 1-я фракция самая тонкая, а N-я — самая крупная;

— треугольная матрица распределения размером N X N; Xi*; Xi3,.. ., kiN — вероятности образования частиц 1-й фракции при разрушении более крупных частиц соответственно 2, 3,.. ., N-й фракций; Х₂₃Д₂₄,.. ., Х₂Л' — вероятности образования частиц 2-й фракции при разрушении более крупных частиц соответственно 3, 4,.. ., N-ik фракций; Яjv-bv — вероятность образования частиц (N — 1)-й фракции при разрушении частиц N-й фракции; {/** *_i} — матрица-столбец размером N X 1 гранулометрического состава измельчаемого материала в (к — 1)-й момент времени;

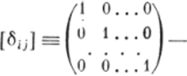
— единичная матрица размером N X N;

{F_l0) — матрица-столбец исходного гранулометрического состава материала, подаваемого на измельчение в первый момент' времени.

Значения элементов матрицы вероятностей разрушения и матрицы распределения определялись в работах [46, 47, 49—51) экспериментально.

Покажем, что математическая модель (2.56) является частным случаем полученной в § 2.1 (неформальным методом структурного упрощения обобщенного математического описания) модели (2.54) процесса измельчения в аппарате идеального смешения периодического действия.

Перейдем от матричной формы записи (2.56) к системе уравнений следующего вида, учитывая правила перемножения матриц:

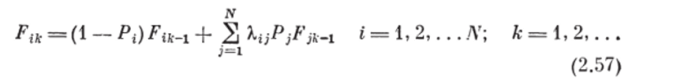
Так как матрица (A, —j] является диагональной, то сумму в правой части (2.57) можно записать в виде.

Причем для i N сумма (2.58) равна нулю (самые крупные частицы могут только разрушаться). С учетом (2.58) система (2.57) записывается следующим образом:

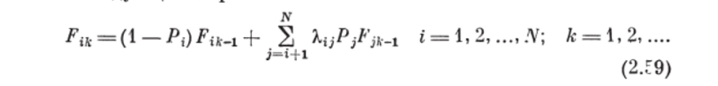
Введем бесконечно малый интервал времени Д/ между (к — 1)-м и к-м моментами времени и разделим на него обе части уравнений (2.59), перейдя к пределу при Дt -+? 0. Тогда получим.

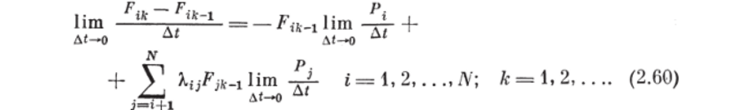
Левая часть (2.60) представляет собой, согласно определению (45Ь производную функции Fi (t) по времени, а выражение Нт (Я*/ДО —.

М—О.

= Ai — вероятность разрушения частицы г-й фракции в единицу времени. С учетом этого (2.60) преобразуется к виду.

Введем теперь бесконечно малый интервал размера частиц Д/ между 1-й и 2-й, 2-й и 3-й,.. (N — 1)-й и ЛГ-й фракциями частиц и разделим на него обе части уравнений (2.61), перейдя к пределу при Д/ 0 и N оо. Тогда получим.

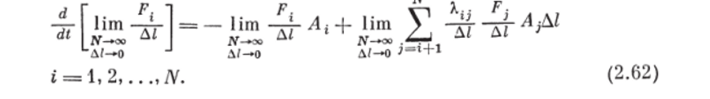
Учитывая выражение определенного интеграла через предел суммы [45), а также то, что Пт (/^/Д/) =/'г (0 — плотность рас;

N— ОО Л/—О пределения числа частиц по размерам, a lirn (А^/Дl) = B₂(li у) — плот;

N—oo

Л1—0

ность распределения вероятности образования частицы размера I при разрушении частицы размера у (у > /), получим уравнение.

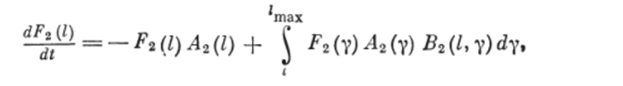
которое описывает процесс измельчения в аппарате идеального смешения периодического действия и непосредственно вытекает, из модели (2.54).