Отношения на множествах

Существуют неполные предложения — предикаты: «меньше, чем…*, «включено в…*, «входит в состав…*, которые образуют отношения на множествах. Математическое отношение — правило, связывающее два или более символических объекта.

Важнейшим в приложениях является класс бинарных отношений, т. е. отношений между двумя объектами. Вся теория графов по существу является теорией бинарных отношений. Говорят, что на множестве М определена бинарная алгебраическая операция, если указан закон R, по которому любой паре элементов а, b е А/, взятых в определенном порядке, однозначно ставится в соответствие некоторый элемент с € М.

Если объекты X и Y находятся в отношении R, это записывается как xRy.

Задание отношения равносильно заданию характеристической функции, равной единице, если отношение существует, и нулю, если не существует. При этом часто используют матричный способ задания отношений.

Матрица бинарного отношения на множестве М = {а^ а^,, а_т) — это квадратная матрица С_т порядка т, в которой элемент Су определяется как.

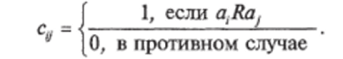
Пример. Задано множество электроприемников М — {I, 2, 3, 4, 5, 6}, которые могут находиться во включенном состоянии в зависимости от особенностей режима работы технологического объекта. Требуется построить матрицу отношения меньше или равно (<).

Решение. Матрица отношения < имеет вид:

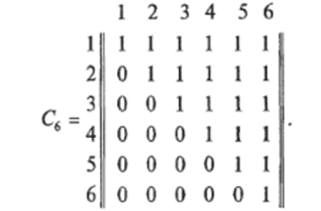
Матрица отношения больше или равно (>) выглядит аналогично, только нули и единицы, за исключением главной диагонали, меняются местами. Матрица отношения равенства (=) единицы содержит только на главной диагонали.

При перестановке членов данного отношения yRx, получаем обратное отношение xR^Ay. Обратное отношение выполняется для коэффициентов трансформации трансформаторов, вертикальной подчиненности управляющих и управляемых структур.

Если выполняются отношения равенства, подобия, одинакового функционального назначения, условий эксплуатации, то для любого объекта х справедлива запись xRx. Такое отношение называется рефлексивным.

Если для любых X и Гиз xRy следует yRx, то отношение называется симметричным. Это отношения равенства (=) или неравенства (^).

Если отношение рефлексивно xRx и симметрично xRy «-* yRx, его называют отношением толерантности х © у.

Если для любых X, Y, Z из xRy и yRz следует xRz, то отношение называется транзитивным. Отношение транзитивности может выполняться для замкнутых сетей различного рода коммуникаций.

Из множества всех отношений выделяется класс отношений одновременно рефлексивных, симметричных и транзитивных. Такие отношения называются отношениями эквивалентности. Эквивалентность — частный случай толерантности. Символ «** обозначает отношение эквивалентности.

Смысл отношения эквивалентности состоит в установлении некоторого сходства, родства между элементами (объектами) по определенному признаку. Отношение эквивалентности должно выполняться для связанных в сеть элементов, подчиняющихся одному центру, выполняющих одинаковые функции и потребляющих однородные ресурсы.

На основании рассмотренных отношений, рассмотрим отношение порядка (, предпочтения) R. Оно используется при сравнении и выборе различных вариантов решений, при решении задач упорядочения каких-либо объектов или их параметров. Отношения являются отношениями нестрогого порядка, а отношения отношениями строгого порядка. Нестрогому порядку, например <, можно сопоставить строгий порядок <, определяемый следующим образом: х < у тогда и только тогда, когда х < у и х Ф у. Отношению строгого порядка, например <, можно сопоставить отношение нестрогого порядка <, тогда и только тогда, когда х < у или х — у. Таким образом, по нестрогому порядку можно найти соответствующий строгий порядок и наоборот.

Множество, на котором задано отношение порядка, называется полностью упорядоченным, если сравнимы любые два его элемента, и частично упорядоченным в противном случае.

Например. отношение подчиненности на предприятии (в фирме) задает строгий частичный порядок, при условии, что работники разных подразделений являются несравнимыми элементами всего множества работников.

Описать отношение предпочтения — значит, каждому исходу х поставить в соответствие такое действительное число v (x), что xRy &# v (x) > v (y), т. е. х не менее предпочтителен, чем у тогда, когда значение функции v для х — v (x) не меньше, чем для у, v (y). При этом равенство v (x) = v (y) соответствует равноценности исходов, а неравенство v (x) > v (y) большей предпочтительности исхода х. Такое представление возможно в том случае, когда любые два исхода сравнимы по отношению предпочтения R; отношение R транзитивно, т. е. из xRy и yRz следует xRz (предпочтения согласованы).

Пример. В таблице указаны номера подстанций и потребляемая подключенными к ним потребителями мощность.

Является ли на множестве Л = {1, 2, 3, 4, 5} отношение «меньше по мощности» отношением порядка?

Решение: не является, поскольку на заданном множестве отсутствует однозначное отношение предпочтения (Si < Si > S3 и т. д.).

Отношение строгого порядка является частным случаем отношения доминирования, (символ ~ «). Между элементами множества X имеет место отношение доминирования, если эти элементы обладают следующими свойствами:

• 1) никакой элемент не может доминировать сам над собой, т. е. утверждение — х «х — ложно;
• 2) в каждой паре элементов х, у только один доминирует над другим, т. е. утверждение — х «у и у «х — является взаимоисключающим.

В отношении доминирования свойство транзитивности не имеет места, поскольку, если х «у, а у «z, это не значит, что х « г.

Множества, на которых кроме операций заданы отношения, называются aiгебраическими системами. Частным случаем алгебраических систем являются модели — множества, на которых заданы только отношения.