Сигналы с аналоговой модуляцией

Долгие годы, но существу начиная с изобретения радио, при передаче информации использовались и до сих пор широко используются аналоговые виды модуляции. Это связано в основном с простотой схемотехнического решения таких видов передачи сигналов. Очевидно, что аналоговые системы еще какое-то время будут существовать наряду с цифровыми системами связи.

При анализе модулированных колебаний и их спектров удобно использовать ряд основных формул тригонометрии:

Сигналы с амплитудной модуляцией. Напомним, что в процессе амплитудной модуляции несущего колебания.

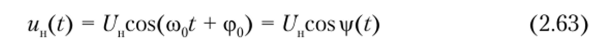
его амплитуда должна изменяться по закону.

где U_n — амплитуда несущей частоты в отсутствие модуляции; со₀ — угловая частота; <�р₀ — начальная фаза; у (?) = со/ + <�р₀ — полная (мгновенная) фаза несущей; k_A — безразмерный коэффициент пропорциональности; e (t) — модулирующий сигнал.

Функцию U_H(t) в теории связи принято называть огибающей амплитудно-модулированного сигнала (АМ-сигнала).

Подставив соотношение (2.64) в формулу (2.63), получим общую формулу АМ-сигнала.

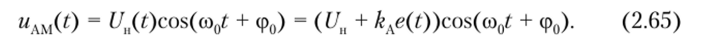
Однотональная амплитудная модуляция. Обратимся к простейшей амплитудной однотональной (от слова «тон» — звук одной частоты), или гармонической, модуляции, когда модулирующий сигнал — гармоническое колебание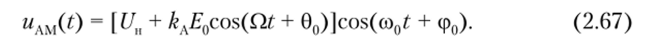

где Е₀ — амплитуда; Q = 2п/Т_{ = 2nF— угловая частота модуляции; F — циклическая частота модуляции; Т_{ — период модуляции; 0_О — начальная фаза.

Процесс амплитудной модуляции осуществляется путем перемножения двух сигналов, поэтому, подчиняясь принципу суперпозиции, является линейной операцией. Подставив соотношение (2.66) в формулу (2.65), получим выражение для АМ-сигнала.

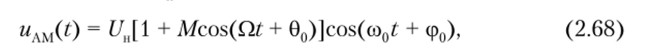
Обозначив через AU=k_AE₀ максимальное отклонение амплитуды АМ-сигнала от амплитуды несущей U_u и проведя несложные выкладки, получим.

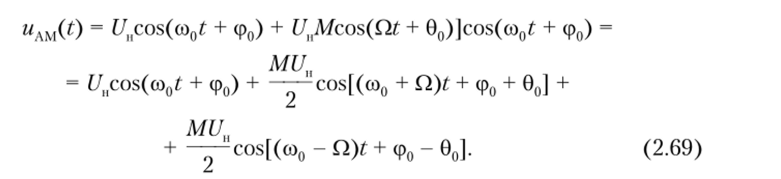
где М = k_AE₀/U_H = A U/U_H — коэффициент, или глубина, амплитудной модуляции.

Отметим, что однотональная модуляция симметрична относительно оси времени.

Спектр АМ-сигнала. Использовав тригонометрическую формулу произведения косинусов, в выражении (2.68) после несложных выкладок получим.

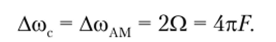
Из формулы (2.69) очевидно, что при однотональной амплитудной модуляции спектр АМ-сигнала состоит из трех высокочастотных составляющих. Первая из них представляет собой исходное несущее колебание с постоянной амплитудой U_u и частотой со₀. Вторая и третья составляющие характеризуют новые гармонические колебания, появляющиеся в процессе амплитудной модуляции и отражающие передаваемый сигнал.

Колебания с частотами со₍₎ + Q и со₀ — Q называются соответственно верхней (upper sideband — USB) и нижней (lower sideband — LSB) боковыми составляющими. Амплитуды боковых составляющих АМ-сигнала одинаковы, равны MUJ2 и расположены симметрично относительно несущей частоты сигнала оз₀.

Реальная ширина спектра АМ-сигнала при однотональной модуляции.

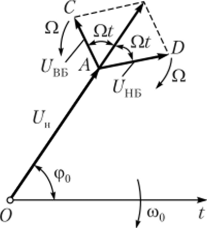
Принцип однотональной амплитудной модуляции показан на рис. 2.26. Графики модулирующего сигнала e (t) с 0_О = 90°, несущего колебания u_u(t) с (р₍₎ = 90° и АМ-сигнала u_AM(t) представлены на рис. 2.26, а — в, а на рис. 2.26, г — е — соответствующие им спектры 5₀(со), ^"((о) и 5^(0). В отсутствие модуляции (М = 0) амплитуды боковых составляющих равны нулю и спектр АМ-сигнала переходит в спектр несущего колебания. При глубине модуляции М < 1 амплитуда АМ-сигнала изменяется от минимального U_m = U_n( 1 — М) до максимального t/_MaKC = U_H( 1 + М) значения. Исключая постоянную U_H, получаем.

Как правило, модулирующий сигнал (см. рис. 2.26, а) является двуполярным. Из графика на рис. 2.26, в можно заметить, что амплитудная огибающая, выделяемая при детектировании, в данном случае оказывается неправильной — она соответствует модулю исходного сигнала. Поэтому при реализации амплитудной модуляции к модулирующему сигналу предварительно добавляют постоянную составляющую U_n, чтобы сделать его однополярным: U_n(t) = U_n + k_Ae (t).

Важное значение для AM-сигналов имеет коэффициент модуляции М. Если при модуляции М> 1, то возникают искажения, называемые перемодуляцией (рис. 2.27). Построим векторную диаграмму при однотональной модуляции несущего колебания. Для упрощения выкладок примем в соотношении (2.69) начальные фазы несущего колебания и модулирующего сигнала ср₀ = 0 и 0_О = 0. При необходимости они могут быть введены в окончательные соотношения. Тогда соотношение (2.69) отразится векторной диаграммой (рис. 2.28), на которой каждая из трех составляющих АМ-сигнала представлена своим вектором.

в

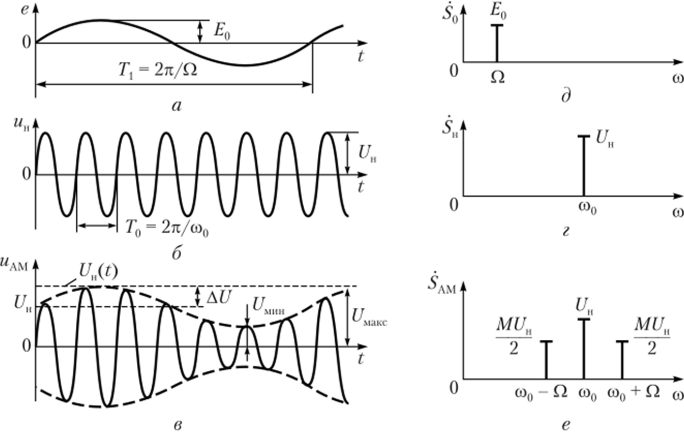
Рис. 2.28. Векторная диаграмма однотонального АМ-сигнала

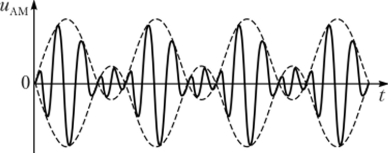
Рис. 2.26. Амплитудная модуляция:

а — модулирующий сигнал; 6 — несущее колебание; в — АМ-сигнал; г — е — соответствующие спектры.

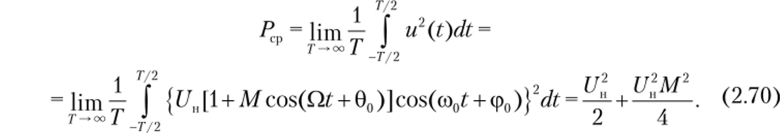
Рис. 2.27. Однотональный АМ-сигнал при перемодуляции

На векторной диаграмме ось времени t вращается по часовой стрелке с угловой скоростью со₀. Поэтому несущее колебание изображается на этой оси вектором О А длиной U_H. Поскольку принято, что угол ср₀ = 0, то ось времени совпала с вектором несущего колебания. Верхняя (U_BB) и нижняя (С/_Нб) боковые составляющие изображаются на диаграмме соответственно векторами АС и AD длиной MUJ2 каждый. Они составляют с направлением вектора несущей О А углы +Q? и вращаются в противоположных направлениях с угловой скоростью Q. Равнодействующим вектором боковых составляющих АС и AD является вектор модуляции АВ. Так как векторы боковых составляющих вращаются в противоположных направлениях с одинаковой угловой скоростью и расположены симметрично относительно вектора Q4, то суммарный вектор ОВ в любой момент времени совпадает с направлением вектора несущего колебания ОА. Длина вектора О В будет периодически изменяться от максимального U_n( 1 + М) до минимального U_u( 1 — М) значений. Если при прохождении через цепи нарушается равенство амплитуд боковых составляющих или симметрия их фаз по отношению фазы несущего колебания, то возникает «качание» вектора модуляции относительно вектора несущей ОА. Это равносильно возникновению паразитной фазовой модуляции.

Энергетические соотношения в AM-сигнале. В соответствии с изменением амплитуды меняется и средняя за период несущей Т₀ = 2тг/со₀ мощность модулированного колебания. Пикам огибающей соответствует мощность в (1 + М)² раз больше мощности несущего колебания. При этом средняя мощность за период модуляции пропорциональна среднему квадрату амплитуды U_H(t), и для ее определения необходимо применить предельный переход.

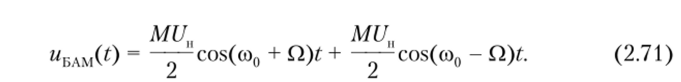
Первое слагаемое в формуле (2.70) не зависит от коэффициента модуляции и равно мощности несущей. Полезная мощность, заключенная в боковых частотах, представлена вторым слагаемым.

Итак, средняя мощность однотонального AM-сигнала за период модуляции Т_{ = 2n/Q превышает мощность несущего колебания в (1 + 0,5 М²) раз. Нетрудно заметить, что доля мощности обеих боковых составляющих AM-сигнала даже при 100%-ной гармонической модуляции (М =1) равна лишь половине мощности несущего колебания. Поскольку передаваемое сообщение заложено только в боковых составляющих AM-сигнала, можно отметить неэффективность использования излучаемой мощности при амплитудной модуляции.

Попытки улучшить характеристики амплитудной модуляции привели к разработке нескольких ее модификаций. Учитывая структуру АМ-сигнала, формирование радиоканальных сигналов можно осуществлять путем передачи:

• • двух боковых полос частот без несущей (балансная амплитудная модуляция);
• • одной боковой полосы частот и несущей;
• • одной боковой полосы частот без несущей;
• • одной боковой полосы, несущей и части второй боковой полосы частот.

Балансная амплитудная модуляция. Первое, что приходит в голову при размышлении на тему повышения энергетических характеристик амплитудной модуляции, — идея удалить бесполезное несущее колебание. Такой способ называется балансной амплитудной модуляцией (БАМ) или амплитудной модуляцией с подавленной несущей (AM-ПН). Выражение для сигнала с балансной амплитудной модуляцией нетрудно получить из формулы (2.69), выбрав для упрощения выкладок фазовые углы ф₀ = 0 и 0_О = 0. Тогда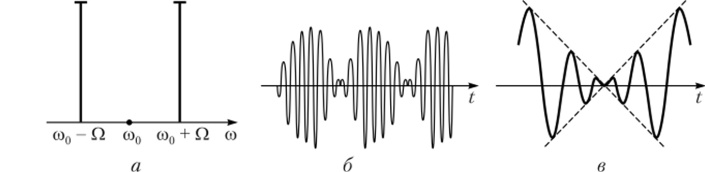

В случае балансной амплитудной модуляции (рис. 2.29) имеет место перемножение двух сигналов — модулирующего и несущего. Это явление и сигнал вида (2.71) называют биениями двух гармонических сигналов с одинаковыми амплитудами MUJ2 и частотами, равными верхней и нижней боковым частотам однотонального AM-сигнала (рис. 2.29, а). Получаемая при биениях разностная частота со_б = со₀ — Q называется частотой биений.

Рис. 2.29. Балансная модуляция:

а — спектр; б — осциллограмма; в — график перехода огибающей через нуль При анализе осциллограммы биений AM-колебания (рис. 2.29, б) может показаться неясным, почему в спектре этого сигнала нет несущей частоты со₀, хотя очевидно наличие высокочастотного заполнения, изменяющегося во времени именно с этой частотой. Такое положение связано с тем, что при переходе огибающей биений через нуль (рис. 2.29, в) фаза высокочастотного заполнения скачком изменяется на 180°, поскольку функция огибающей cosQ? имеет разные знаки слева и справа от нуля. Если этот сигнал подать на высокодобротную колебательную систему, настроенную на частоту со₀, то выходной эффект будет очень мал, стремясь к нулю при возрастании добротности. Колебания в системе, возбужденные одним периодом биений, будут гаситься последующим периодом. Именно так с физических позиций принято рассматривать вопрос о реальном смысле спектрального состава сигнала с БАМ.

Ширина спектра AM-сигнала с подавленной несущей такая же, как при обычной амплитудной модуляции. При многотональной балансной модуляции выражение AM-сигнала с подавленной несущей содержит две симметричные группы верхних и нижних боковых колебаний.

Итак, амплитудная модуляция с подавленной несущей обладает определенными преимуществами по сравнению с обычной амплитудной модуляцией. Однако этот способ модуляции не получил широкого распространения, что связано с проблемами, возникающими при детектировании радиосигнала.

Однополосная амплитудная модуляция. Под ней подразумевается передача одной боковой полосы частот и несущей. Большое значение для радиосвязи имело изобретение амплитудной модуляции с одной боковой полосой (ОБП; single side band — SSB), сделанное в 1915 г. В современных системах радиосвязи часто приходится экономить не только мощность, но и полосу занимаемых частот. Как уже отмечалось, спектры двух боковых полос AM-сигнала являются зеркальным отражением друг друга относительно несущей частоты, г. е. они несут одну и ту же информацию. Поэтому одну из боковых полос можно удалить. В результате получается колебание с несущей и одной боковой полосой. В более общем случае под сигналами с одной боковой полосой, или сигналами однополосной модуляции (ОМ), понимают колебания, полученные при модуляции гармонической несущей частоты и отличающиеся тем, что их спектр (на положительных частотах) располагается по одну сторону (слева или справа) от несущей со = со₍₎. Сигналы с однополосной амплитудной модуляцией занимают полосу частот в два раза более узкую, чем обычный АМ-сигнал.

По внешним характеристикам сигнал с одной боковой полосой и несущей напоминает обычный АМ-сигнал. В зависимости от того, какая боковая полоса сохраняется, говорят об однополосной модуляции с использованием верхней или нижней боковой составляющей (полосой). В частности, однотональный ОБП-сигнал с подавленной нижней боковой составляющей и начальными фазами несущей ср₀ = 0 и модулирующего колебания 0_О = О записывается в виде.

Каждый из членов правой части формулы (2.72) представляет собой произведение двух функций, одна из которых изменяется во времени медленно (отражает модулирующий сигнал), а другая — быстро (отражает несущее колебание).

Итак, сигнал с ОБП можно представить суммой двух AM-сигналов с одинаковыми несущими, но сдвинутыми по фазе друг относительно друга на 90°. Амплитудными функциями AM-сигналов являются модулирующий сигнал и его квадратурное дополнение. В зависимости от того, складываются эти сигналы или вычитаются (а точнее, какая из несущих опережает другую по фазе), формируется однополосный сигнал с верхней или нижней боковой полосой. По существу при однополосной модуляции происходит сдвиг спектра передаваемого сигнала в окрестность несущей частоты. В отличие от обычной амплитудной модуляции каждая «половинка» спектра смещается в своем направлении: область положительных частот — к +со₀, а область отрицательных частот — ксо₀. При формировании сигнала с нижней боковой полосой спектр модулирующего сигнала инвертируется (зеркально поворачивается вдоль оси частот).

Учитывая, что «быстрые» сомножители находятся в квадратуре (сдвинуты, но фазе на 90°), вычислим медленно изменяющуюся огибающую ОБП-сигнала:

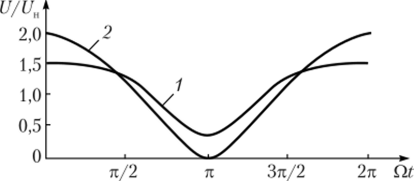
Временная диаграмма огибающей ОБП-сигнала, рассчитанная по формуле (2.73) при глубине модуляции М = 1, показана на рис. 2.30 (кривая 1). Здесь же для сравнения построена огибающая однотонального АМ-сигнала (кривая 2), тоже при М = 1. Сравнение кривых показывает, что непосредственное детектирование ОБП-сигнала, но огибающей будет сопровождаться значительными искажениями. Исходная информация на приеме будет образовываться от взаимодействия переданных боковой полосы частот и несущей. Однако для подавления одной из боковых полос надо использовать сложные в реализации канальные фильтры.

Рис. 230. Огибающие однотональных модулированных сигналов при М = 1:

1 — ОБП-сигнала; 2 — АМ-сигнала Другой, более эффективной с точки зрения энергетических показателей разновидностью AM-сигналов является однополосная амплитудная модуляция с подавленной несущей (ОБП-ПН):

Данный вид амплитудной модуляции представляет собой такое преобразование несущего колебания, при котором спектр радиосигнала полностью совпадает со спектром сообщения, перенесенным по оси частот в высокочастотную область нижней или верхней боковой полосы.

Передача одной боковой полосы без несущей обеспечивает минимально возможную ширину спектра канального сигнала, равную ширине спектра исходного сигнала, что позволяет наиболее экономно реализовать линейный спектр сигнальной полосы. Передачу одной боковой полосы частот, несущей и части второй боковой полосы частот используют, когда спектр исходного сигнала начинается от частот, близких к нулю. К таким сигналам относят телевизионный сигнал. При реализации этого метода канальный фильтр должен иметь кососимметричную характеристику коэффициента передачи относительно несущей частоты.

На практике однотональные AM-сигналы используются либо для учебных, либо для исследовательских целей. Реальный же модулирующий сигнал имеет сложный спектральный состав. Математически такой сигнал, состоящий из N гармоник, можно представить тригонометрическим рядом.

Здесь амплитуды гармоник сложного модулирующего сигнала E_t произвольны, а их частоты образуют упорядоченный спектр Q, < 0₂< … < Q, < … < Q_jV. В отличие от ряда Фурье частоты Q, не обязательно кратны друг другу.

Подставляя ряд (2.74) в формулу (2.65), после несложных преобразований получим выражение AM-сигнала с начальной фазой несущего ср₍₎ = О.

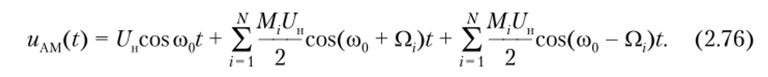
i=i.

где Mj = к_АЕ_}/11_п — совокупность парциальных (частичных) коэффициентов модуляции.

Эти коэффициенты характеризуют влияние гармонических составляющих модулирующего сигнала па общее изменение амплитуды высокочастотного колебания. Воспользовавшись тригонометрической формулой произведения двух косинусов и проделав несложные преобразования, запишем формулу (2.75) в виде.

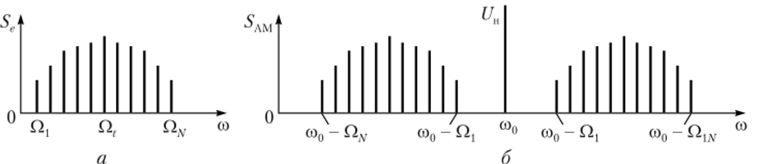
Из формулы (2.76) очевидно, что в спектре сложного AM-сигнала наряду с несущим колебанием содержатся группы верхних и нижних боковых составляющих, являющихся масштабными копиями спектра модулирующего сигнала и расположенных симметрично относительно частоты со₀. Отсюда следует важный вывод: ширина спектра сложного AM-сигнала равна удвоенному значению наивысшей частоты в спектре модулирующего сигнала Q_v, т. е. Асо_с = Асо_лм = 2Q_V.

На рис. 2.31 показаны спектральные диаграммы при модуляции несущего колебания сложным модулирующим сигналом. Очевидно, что модулирующий сигнал 5,(со) (Р^ис— 2.31, а) в AM-сигнале 5_лм(со) расположен, но обе стороны от несущей U_n (рис. 2.31, б).

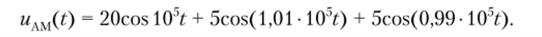
Рис. 2.31. Спектральные диаграммы при модуляции сложным сигналом:

а — модулирующего сигнала; 6 — АМ-сигнала Пример 2.5.

Определим спектральный состав и запишем аналитическое выражение АМсигнала и_ам(?) = 20(1 + 0,5 cos10³?)cos10⁵?.

Решение

Воспользовавшись соотношением (2.68), находим, что несущая частота со₀ = = 10⁵; частота модуляции Q = 10, боковые частоты со₀ + Q = 1,01 • 10, со₀ — Q = = 0,99 • 10, амплитуда несущей U_n = 20 В; коэффициент модуляции М = 0,5. Следовательно, в соответствии с формулой (2.68)

Приведенные рассуждения справедливы не только для дискретного спектра, но и для любого вида спектра передаваемого сообщения. Можно считать, что спектр модулирующего сигнала заключен под огибающей заданного вида. В этом случае спектральная плотность передаваемого AM-сигнала состоит из двух симметричных идентичных всплесков спектра модулирующего сигнала S_e(со) относительно несущей частоты со₀. Значит, для определения спектра AM-сигнала достаточно сдвинуть на частоту со₀ огибающую спектра исходного колебания.

В настоящее время амплитудная модуляция применяется для радиовещания на сравнительно низких частотах (в диапазонах от километровых до декаметровых волн) и для передачи изображения в телевизионном вещании.

Сопоставление сигналов с вариантами амплитудной модуляции. На рис. 2.32 показаны диаграммы сигналов и их спектров с вариантами однотональной амплитудной модуляции: AM, БАМ и ОБП (на эпюрах /₀ = = 2л/со₀ = 1 /Т₀ — циклическая частота несущей; F= 2n/Q = 1/7″ — циклическая частота модулирующего гармонического сигнала).

Как очевидно из сопоставления эпюр на рис. 2.32, а, б ив, г, устранение несущего колебания в AM-сигнале приводит к существенным изменениям.

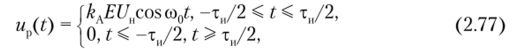
Рис. 232. Эпюры сигналов и их спектров с вариантами амплитудной модуляции:

о, б — AM-сигнала; в, г — БАМ-сигнала; д, е — ОБП-сигнала огибающей модулированного колебания, которая перестает копировать модулирующий сигнал. Это обстоятельство усложняет детектирование принятого сигнала — определение модулирующего сигнала при приеме балансно-модулированного колебания. Если убрать и нижнюю боковую частоту (получится модуляция с одной боковой полосой — ОБП), то спектр демонстрирует экономное использование отведенной полосы и мощности передатчика системы радиосвязи (рис. 2.32, д, е), но вместо модулированного колебания получится гармоническое с частотой, равной частоте верхней боковой /₀ + F. Для того чтобы иродетектировать такое колебание, надо определить амплитуду и частоту модулирующего сигнала.

Наибольшие проблемы возникают при определении частоты модулирующего сигнала, поскольку надо знать частоту несущего колебания. Есть несколько вариантов решения этой проблемы. Например, можно непрерывно передавать в точку приема это несущее колебание с сильно уменьшенной амплитудой (в виде так называемого пилот-сигнала). Несущее колебание можно также передавать периодически, синхронизируя этими «всплесками» генератор несущей в точке приема (так передают информацию о частоте и фазе цветовой поднесущей в системах цветного телевидения). Однако сложность процесса детектирования окупается более эффективным использованием полосы рабочих частот.

Сигналы с амплитудно-импульсной модуляцией. В теории связи широко применяют различные модулированные импульсные последовательности, среди которых следует выделить последовательности прямоугольных радиоимпульсов (рис. 2.33). Вычислим спектр радиоимпульса, полученного при амплитудной модуляции гармонического несущего колебания одиночным импульсом амплитудой Е и длительностью т_и (рис. 2.33, а). Его спектральная плотность определяется формулой (2.33) и имеет вид функции sinje/x. Запишем для прямоугольного радиоимпульса:

где k_A — безразмерный коэффициент пропорциональности.

Определим спектральную плотность прямоугольного радиоимпульса и сравним ее со спектральной плотностью подобного видеоимпульса. Спе;

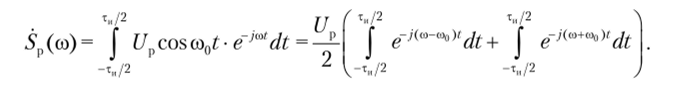
Рис. 233. Импульсные сигналы:

а — видеоимпульс; б — радиоимпульс ктральную плотность радиоимпульса вычислим, применив к выражению (2.77) прямое преобразование Фурье (2.29). Примем k_AEU_U = U и запишем спектральную плотность:

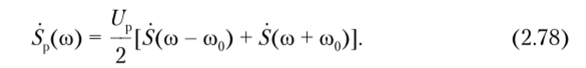
В этом соотношении первый интеграл определяет спектральную плотность исходного видеоимпульса с амплитудой Е = 1 при частоте со — со₀, а второй — ту же спектральную плотность, но при частоте со + со₀. Поэтому последнее выражение можно записать в следующей форме:

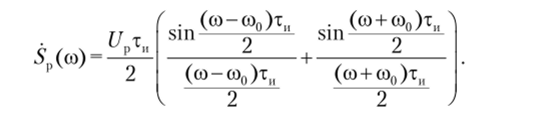
Подставляя значение спектральной плотности импульса из соотношения (2.33) в формулу (2.78), получим спектральную плотность радиоимпульса.

На рис. 2.34 представлены диаграммы спектральных плотностей соответственно модулирующего видеоимпульса и аналогичного ему по огибающей радиоимпульса. Как нетрудно заметить из приведенных графиков, спектральная плотность радиоимпульса полностью повторяет по форме спектральную плотность модулирующего импульса. Основное отличие спектральной плотности видеоимпульса (рис. 2.34, а) от спектральной плотности радиоимпульса той же формы — наличие сдвига спектральной плотности радиоимпульса по оси частот по обе стороны от начала координат на значение несущей ±со₀ (рис. 2.34, б).

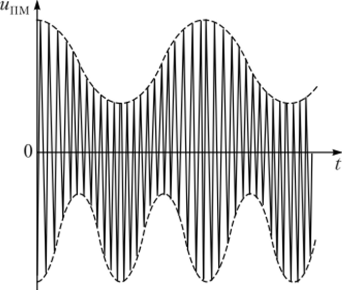
Рис. 2.34. Спектральные диаграммы:

а — видеоимпульса; 6 — радиоимпульса Полярная модуляция в стереофоническом вещании. В 1939 г. инженер А. И. Косцов изобрел еще один вид аналоговой амплитудной модуляции сигналов, названный полярной модуляцией (ПМ). Сигналы не являются колебаниями с совершенно новым видом модуляции. Это скорее демопстрация применения разновидности амплитудной модуляции для решения конкретной технической задачи. Речь пойдет о реализации стереофонии в радиовещании метрового и дециметрового диапазонов и в различных устройствах звукового сопровождения (телевидении, видеосвязи и т. п.). В радиовещании наряду с монофоническими (от греч. monos — один) все чаще используются стереофонические (от греч. stereos — объемный) системы. Субъективное качество восприятия человеком стереофонической программы значительно выше, чем монофонической. Достаточно хороший стереоэффект получается при двухканальной передаче звука. В принципе стереофонический радиоканал можно получить, объединив два монофонических канала, но одному из которых передается сигнал l (t) = EjCos Qt от левого источника звука, а по другому — сигнал r (t) = E_rcosCl_rt от правого источника. Однако при этом не достигается совместимость стереофонической системы радиовещания с монофоническими приемниками.

Совместимое с монофоническим стереофоническое радиовещание создают, используя полярную модуляцию. Типичная осциллограмма сигнала с полярной модуляцией представлена на рис. 2.35. Получающийся сигнал (его называют композитным стереосигналом) благодаря наличию низкочастотных составляющих обладает интересным свойством: его верхняя (положительная) и нижняя (отрицательная) огибающие не совпадают, но частоте. Более того, каждая из них с точностью до постоянной составляющей соответствует сигналу одного из стереоканалов: верхняя (положительные значения) огибающая — это левый канал, а нижняя (отрицательные значения) — правый. Такая структура передаваемого сигнала позволяет в приемнике легко выделить из него сигналы стереоканалов. Для осуществления совместимого с монофоническим стереовещания необходимо передавать сигналы l (t) (левого) и r (t) (правого) каналов, но одной линии связи одновременно.

При разработке системы такого вещания накладывается еще и требование совместимости с уже имеющимися монофоническими приемниками. Поэтому для стереовещания модифицируется низкочастотный модулирующий сигнал, который поступает на вход модулятора передатчика (используется угловая модуляция). В стереофонической системе сигналы звука правого l (t) и левого r (t) каналов преобразуются в суммарно-разностном преобразователе в суммарные и разностные колебания. Низкочастотная составляющая сигнала модуляции, лежащая в звуковом диапазоне, для сов;

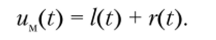
Рис. 235. Стереофонический сигнал с полярной модуляцией

местимости с монофоническими приемниками должна представлять монофонический сигнал, т. е. сумму сигналов левого и правого каналов:

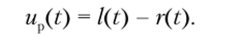
В области более высоких (ультразвуковых) частот модулирующего сигнала с помощью амплитудной модуляции передается дополнительный сигнал, позволяющий впоследствии выделить из полученной смеси сигналы /(?) и r (t) по отдельности. Поскольку монофонический сигнал — это сумма двух каналов, дополнительным компонентом, позволяющим восстановить исходные сигналы двух каналов, надо выбрать их разность:

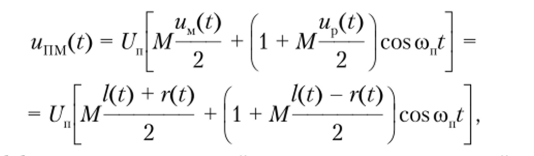
Разностный сигнал модулирует по амплитуде вспомогательное поднесущее высокочастотное колебание u_n(t) = U_ncos со/, где U_n и со_п — амплитуда и частота. Сумма модулированной разностным сигналом поднесущей и монофонического сигнала ujj) образует полярно-модулированное колебание. Для формирования такого сигнала используют суммарно-разностный метод. Действительно, нужное свойство передаваемого колебания будет реализовано, если скомбинировать монофонический ujj) и разностный u_p(t) сигналы следующим образом:

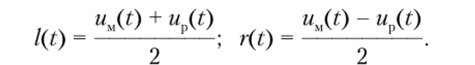
где М — коэффициент амплитудной модуляции, одинаковый в обоих каналах.

Если cos со_п? = 1, то u_nM(t) = U_n( 1 + Ml (t)), т. е. верхняя огибающая полярио-модулированного колебания действительно отражает сигнал /(?) левого канала. Если же cosco_n? = -1, то напряжение u_UM(t) = U_n( 1 — Mr (t)); значит, нижняя огибающая соответствует правому каналу r (t). В отсутствие перемодуляции огибающие имеют разные знаки и могут быть без труда разделены в приемнике.

Выделяя, а затем складывая и вычитая колебания ujj) и гг_р(?), можно восстановить сигналы левого и правого каналов:

Использование поднесущей частоты. Необходимо заметить, что в изображении на рис. 2.35 сигнал для передачи не используется. Дело в том, что из-за наличия несущего колебания «размах» сигнала (суммарная величина максимальных отклонений в сторону положительных и отрицательных значений) сильно увеличивается по сравнению с монофоническим сигналом, что технически нежелательно. Поэтому несущее колебание частично или полностью подавляют, так что разностный сигнал передается в режиме перемодуляции.

Непосредственно сигналы с полярной модуляцией в вещании нельзя применять, поскольку они содержат низкочастотную (звуковую) составляющую, пропорциональную полусумме колебаний левого и правого каналов. Поэтому переходят к двухступенчатому процессу. Вначале формируют сигнал с полярной модуляцией, выбрав в качестве частоты со_п поднесущую частоту, лежащую значительно выше верхней границы передаваемого звукового диапазона. Потом проводят частотную модуляцию несущего колебания, частота которого соответствует метровому или дециметровому диапазону волн. В качестве модулирующего колебания используют полярно-модулированный сигнал, полученный на первом этапе.

При детектировании такого колебания в обычном монофоническом приемнике полу разностный сигнал не воспроизводится, поскольку его спектр расположен в окрестности поднесущей частоты, т. е. за пределом звукового диапазона. Полусуммарный сигнал поступает на выход приемника и обеспечивает вполне приемлемое качество звучания.

Стандарты стереофонического радиовещания в России и зарубежом отличаются друг от друга. Принятый у нас стандарт устанавливает частоту поднесущего колебания 31,25 кГц. Для эффективного использования радиоканала в передатчике поднесущее колебание ослабляют по амплитуде в пять раз, а в приемнике за счет специальных схемных решений восстанавливают этот сигнал до исходного уровня. Такая мера связана с тем, что по стандарту девиация частоты не может превышать 50 кГц. Если использовать этот ресурс для передачи вспомогательного поднесущего колебания, то возможно ухудшение качества воспроизведения звуковых колебаний и прежде всего снижение их громкости. Американский и европейский стандарты решают эту задачу по-другому. Частота поднесущего колебания там выбирается равной 38 кГц. Это колебание подавляется в передатчике полностью, а вместо него в состав модулирующего сигнала вводят так называемый пилот-тон на частоте 19 кГц. В приемнике частота пилот-тона удваивается, и за счет этого происходит восстановление поднесущего.